《2025年1加1轻巧夺冠完美期末七年级数学上册北师大版辽宁专版》

21. （8 分）（沈阳铁西期末）
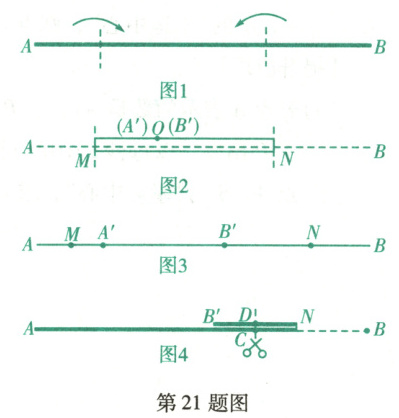
如图 1，将一段长为 60 cm 的绳子$AB$拉直铺平后折叠（绳子无弹性，折叠处长度忽略不计），使绳子与自身一部分重叠.
（1）若将绳子$AB$沿点$M$，$N$折叠，点$A$，$B$分别落在点$A'$，$B'$处.
①如图 2，若点$A'$，$B'$恰好重合于点$O$处，求$MN$的长；
②如图 3，若点$A'$落在点$B'$的左侧，且$A'B' = 20$ cm，求$MN$的长.
（2）如图 4，若将绳子$AB$沿点$N$折叠后，点$B$落在点$B'$处，在重合部分$B'N$上用剪刀沿与绳子垂直方向将绳子剪断，把绳子分为$AC$，$CD$，$B'D$三段，且使这三段绳子的长度由短到长的比为 3 : 4 : 5，请设计裁剪方案（即求此时绳子$AN$的长，写出 1 种方案即可）.

答案： 21.解：
(1)①由题意得$A'M + B'N = MN$，$MN = AB - A'M - B'N = 30(cm)$.
②$\because AM + A'M + A'B'+B'N + BN = 60(cm)$，$A'B' = 20 cm$，$AM = A'M$，$B'N = BN$，$\therefore A'M + B'N = 20 cm$，$MN = A'M + A'B'+B'N = 40 cm$.
(2)根据题意得$CN = DN=\frac{1}{2}CD$，使得$AC$，$CD$，$B'D$这三段绳子的长度由短到长的比为$3:4:5$，$\therefore$三段绳长由短到长分别为$15 cm$，$20 cm$，$25 cm$，分六种情况：①当$B'D:AC:CD = 3:4:5$时，$AC=\frac{1}{3}AB$，$CD=\frac{5}{12}AB$，$\therefore AN=\frac{1}{3}AB+\frac{1}{2}CD=\frac{13}{24}AB = 32.5(cm)$；②当$B'D:CD:AC = 3:4:5$时，$AC=\frac{5}{12}AB$，$CD=\frac{1}{3}AB$，$\therefore AN=\frac{5}{12}AB+\frac{1}{2}CD=\frac{7}{12}AB = 35(cm)$；③当$CD:B'D:AC = 3:4:5$时，$AC=\frac{5}{12}AB$，$CD=\frac{1}{4}AB$，$\therefore AN=\frac{5}{12}AB+\frac{1}{2}CD=\frac{13}{24}AB = 32.5(cm)$；④当$CD:AC:B'D = 3:4:5$时，$AC=\frac{1}{3}AB$，$CD=\frac{1}{4}AB$，$\therefore AN=\frac{1}{3}AB+\frac{1}{2}CD=\frac{11}{24}AB = 27.5(cm)$；⑤当$AC:B'D:CD = 3:4:5$时，$AC=\frac{1}{4}AB$，$CD=\frac{5}{12}AB$，$\therefore AN=\frac{1}{4}AB+\frac{1}{2}CD=\frac{11}{24}AB = 27.5(cm)$；⑥当$AC:CD:B'D = 3:4:5$时，$AC=\frac{1}{4}AB$，$CD=\frac{1}{3}AB$，$\therefore AN=\frac{1}{4}AB+\frac{1}{2}CD=\frac{5}{12}AB = 25(cm)$.
综上所述，$AN$的长度为$32.5 cm$或$35 cm$或$27.5 cm$或$25 cm$.（写出$1$种方案即可）