《2025年新课程学习与检测七年级数学上册》

9. 如图所示,几块大小不等的正方形纸片$A,B,·s,I$无重叠地铺满了一块长方形.已知正方形纸片$E$的边长为$7$,求其余正方形的边长.

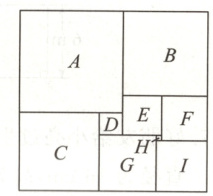
答案： 9.解：设中间正方形H的边长为x，则F的边
长为7+x，B的边长为14+x，I的边长为
7+2x，G的边长为7+3x，D的边长为4x，
C的边长为7x+7，A的边长=B的边长+
7-D的边长=21-3x，或者A的边长=C
的边长+D的边长=7+11x，
∴21-3x=7+11x，解得x=1.
∴7+x=8，14+x=15，7+2x=9，7+3x=
10，4x=4，7x+7=14，21-3x=18.
答：其余正方形的边长为18，15，14，10，9，
8，4，1.

10. 用一元一次方程解决下列问题:
如图所示,在同一水平桌面上放置了甲、乙两个长方体容器.容器甲的底面积为$60\mathrm{d}{\mathrm{m}}^{2}$,高为$8\mathrm{d}\mathrm{m}$;容器乙的底面积为$40\mathrm{d}{\mathrm{m}}^{2}$,高为$12\mathrm{d}\mathrm{m}$.已知容器甲中盛满了水,而容器乙中目前的水位高度为$2\mathrm{d}\mathrm{m}$.现利用抽水装置从容器甲向容器乙匀速注水,每分钟注水$20\mathrm{d}{\mathrm{m}}^{3}$.
(1) 从容器甲开始向容器乙注水起,经过多长时间,甲、乙两个容器中水位的高度相等?
(2) 经过多长时间,甲、乙两个容器中水位的高度相差$2\mathrm{d}\mathrm{m}$?

答案： 10.解：
(1)设经过x min，甲、乙两个容器中水
位的高度相等，
根据题意得$8-\frac{20}{60}x=2+\frac{20}{40}x，$解得$x=\frac{36}{5}.$
答：经过$\frac{36}{5}min，$甲、乙两个容器中水位的高
度相等.
(2)设经过y min，甲、乙两个容器中水位
的高度相差2 dm，
根据题意得$8-\frac{20}{60}y=2+\frac{20}{40}y+2$或$8-\frac{20}{60}y=2+\frac{20}{40}y-2，$
解得$y=\frac{24}{5}$或$y=\frac{48}{5}.$
答：经过$\frac{24}{5}min$或$\frac{48}{5}min，$甲、乙两个容器
中水位的高度相差2 dm.

1. 某次数学竞赛共有 15 道题目，已知选对一道得 4 分，选错一道或者不选扣 2 分。某同学最后的得分是 36 分，则他选对的题目有(B)

A.10 道
B.11 道
C.12 道
D.13 道

答案： 1.B

2. 某同学买 80 分邮票与 1 元邮票共花 16 元，已知买的 1 元邮票比 80 分邮票少 2 枚，设买 80 分邮票 $ x $ 枚，则根据题意可列方程为(A)

A.$ 0.8x+(x - 2)=16 $
B.$ 0.8x+(x + 2)=16 $
C.$ 80x+(x - 2)=16 $
D.$ 80x+(x + 2)=16 $

答案： 2.A

3. 学校组织植树活动，已知在甲处植树的有 23 人，在乙处植树的有 17 人，现调 20 人去支援，使在甲处植树的人数是乙处植树人数的 2 倍。设应调往甲处 $ x $ 人，则可列方程为(B)

A.$ 2(23 + x)=17 + 20 - x $
B.$ 23 + x=2(17 + 20 - x) $
C.$ 23 + x=2(17 + x) $
D.$ 23 + 20 - x=2(17 + x) $

答案： 3.B