2025年新课程学习与检测七年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程学习与检测七年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
4. 不透明的袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有 4 个面是三角形;乙同学:它有 8 条棱.该模型对应的立体图形可能是(
A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
D
)A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
答案:
4.D
5. 下列说法错误的是(
A.长方体是四棱柱
B.三棱锥的底面是三角形
C.$n$ 棱柱有 $n$ 个面,$2n$ 个顶点,$3n$ 条棱
D.若直棱柱的底面边长都相等,则它的各个侧面的面积相等
C
)A.长方体是四棱柱
B.三棱锥的底面是三角形
C.$n$ 棱柱有 $n$ 个面,$2n$ 个顶点,$3n$ 条棱
D.若直棱柱的底面边长都相等,则它的各个侧面的面积相等
答案:
5.C
6. 下列几何体中,可以组成如图所示的陀螺的是(

A.长方体和圆锥
B.长方形和三角形
C.圆和三角形
D.圆柱和圆锥
D
)
A.长方体和圆锥
B.长方形和三角形
C.圆和三角形
D.圆柱和圆锥
答案:
6.D
7. 一个七棱柱一共有________条棱,有________个面,有________个顶点.
答案:
7.21 9 14
8. 如图所示,从一个棱长为 3 cm 的正方体的一顶点处挖去一个棱长为 1 cm 的正方体,则剩余部分的表面积是

54 $cm^{2}$
.
答案:
8.54 $cm^{2}$
9. 如图所示,这是一个六棱柱,它的底面边长都是 6 cm,高是 4 cm.
(1)这个棱柱共有多少个顶点?
(2)这个棱柱共有多少条棱?所有棱长的和是多少?
(3)这个棱柱的侧面积是多少?

(1)这个棱柱共有多少个顶点?
(2)这个棱柱共有多少条棱?所有棱长的和是多少?
(3)这个棱柱的侧面积是多少?

答案:
9.
(1)共有12个顶点.
(2)共有18条棱,所有棱长的和是$12×6 + 6×4 = 96(cm)$.
(3)侧面积为$6×6×4 = 144(cm^{2})$.
(1)共有12个顶点.
(2)共有18条棱,所有棱长的和是$12×6 + 6×4 = 96(cm)$.
(3)侧面积为$6×6×4 = 144(cm^{2})$.
10. 18 世纪瑞士数学家欧拉证明了简单多面体中顶点数($V$)、面数($F$)、棱数($E$)之间存在的一个有趣的关系式,这个关系式被称为欧拉公式.请观察下列几种简单多面体模型,解答下列问题.
(1)根据上面的多面体模型,填写表格并进行推测.

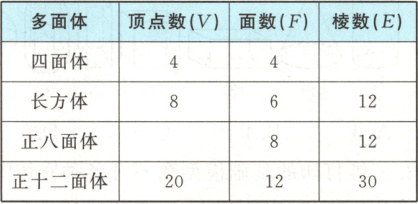
推测:顶点数($V$)、面数($F$)、棱数($E$)之间存在的关系式是
(2)一个多面体的面数比顶点数小 8,且有 30 条棱,则该多面体的顶点数是
(3)某个玻璃饰品的外形是简单多面体,它的外表由三角形和八边形两种多边形拼接而成,且有 48 个顶点,每个顶点处都有 3 条棱.设该多面体表面三角形的个数为 $x$,八边形的个数为 $y$,求 $x + y$ 的值.
(1)根据上面的多面体模型,填写表格并进行推测.


推测:顶点数($V$)、面数($F$)、棱数($E$)之间存在的关系式是
$V + F - E = 2$
.(2)一个多面体的面数比顶点数小 8,且有 30 条棱,则该多面体的顶点数是
20
.(3)某个玻璃饰品的外形是简单多面体,它的外表由三角形和八边形两种多边形拼接而成,且有 48 个顶点,每个顶点处都有 3 条棱.设该多面体表面三角形的个数为 $x$,八边形的个数为 $y$,求 $x + y$ 的值.
答案:
10.
(1)6 6 $V + F - E = 2$
(2)20 解析:由
(1)可知$V + F - E = 2$.
∵多面体的面数比顶点数小8,且有30条棱,
∴$V + V - 8 - 30 = 2$,解得$V = 20$.
(3)解:
∵多面体有48个顶点,每个顶点处都有3条棱,两点确定一条直线,
∴多面体的棱共有$48×3÷2 = 72$(条).
设总面数为$F$,
则$48 + F - 72 = 2$,解得$F = 26$,
∴$x + y = 26$.
(1)6 6 $V + F - E = 2$
(2)20 解析:由
(1)可知$V + F - E = 2$.
∵多面体的面数比顶点数小8,且有30条棱,
∴$V + V - 8 - 30 = 2$,解得$V = 20$.
(3)解:
∵多面体有48个顶点,每个顶点处都有3条棱,两点确定一条直线,
∴多面体的棱共有$48×3÷2 = 72$(条).
设总面数为$F$,
则$48 + F - 72 = 2$,解得$F = 26$,
∴$x + y = 26$.
查看更多完整答案,请扫码查看


