2025年1加1轻巧夺冠完美期末七年级数学上册人教版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末七年级数学上册人教版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (8分)(大连金普期末)
已知$\angle AOB(0^{\circ}<\angle AOB < 180^{\circ})$与$\angle COD$共顶点$O$,点$A$,$O$,$C$在一条直线上,$\angle AOB = 2\angle COD$,$OM$为$\angle AOD$的平分线,$ON$为$\angle COB$的平分线.
(1)填空:$\angle AOC =$
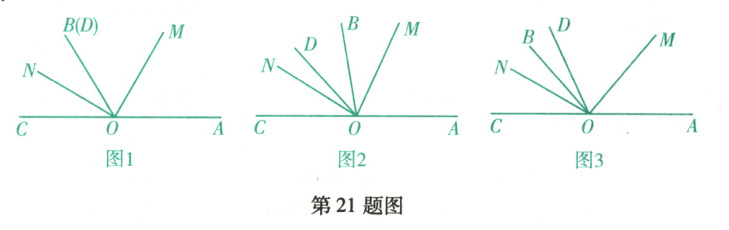
(2)如图1,当$OB$,$OD$重合时,求$\angle MON$的度数.
(3)如图2,当$\angle AOB + \angle COD < 180^{\circ}$时,若$\angle COD = 50^{\circ}$,求$\angle MON$的度数.
(4)如图3,当$\angle AOB + \angle COD > 180^{\circ}$时,探究$\angle MON$与$\angle COD$之间的数量关系,并加以说明.
已知$\angle AOB(0^{\circ}<\angle AOB < 180^{\circ})$与$\angle COD$共顶点$O$,点$A$,$O$,$C$在一条直线上,$\angle AOB = 2\angle COD$,$OM$为$\angle AOD$的平分线,$ON$为$\angle COB$的平分线.
(1)填空:$\angle AOC =$
180°
。(2)如图1,当$OB$,$OD$重合时,求$\angle MON$的度数.
(3)如图2,当$\angle AOB + \angle COD < 180^{\circ}$时,若$\angle COD = 50^{\circ}$,求$\angle MON$的度数.
(4)如图3,当$\angle AOB + \angle COD > 180^{\circ}$时,探究$\angle MON$与$\angle COD$之间的数量关系,并加以说明.

答案:
21.解:
(1)180°
(2)当OB,OD重合时,∠AOD+∠COB=180°,
∵OM为∠AOD的平分线,ON为∠COB的平分线,
∴∠AOM=∠BOM=$\frac{1}{2}$∠AOD,∠CON=∠DON=$\frac{1}{2}$∠COB,
∴∠MON=∠BOM+∠DON=$\frac{1}{2}$(∠AOD+∠COB)=90°.
(3)
∵∠COD=50°,
∴∠AOB=2∠COD=100°,
∴∠COB=180°-100°=80°,∠AOD=180°-50°=130°,
∵OM为∠AOD的平分线,ON为∠COB的平分线,
∴∠AOM=$\frac{1}{2}$∠AOD=65°,
∠CON=$\frac{1}{2}$∠COB=40°,
∴∠MON=180°-∠AOM-∠CON=180°-65°-40°=75°.
(4)∠MON=$\frac{3}{2}$∠COD,理由如下:设∠COD=x,则∠AOB=2∠COD=2x,
∴∠AOD=180°-x,
∠COB=180°-2x,
∵OM为∠AOD的平分线,ON为∠COB的平分线,
∴∠AOM=$\frac{1}{2}$∠AOD=90°-\frac{1}{2}x,∠CON=$\frac{1}{2}$∠COB=90°-x,
∴∠MON
=180°-∠AOM-∠CON=180°-90°+\frac{1}{2}x=90°+\frac{3}{2}x=\frac{3}{2}∠COD.
(1)180°
(2)当OB,OD重合时,∠AOD+∠COB=180°,
∵OM为∠AOD的平分线,ON为∠COB的平分线,
∴∠AOM=∠BOM=$\frac{1}{2}$∠AOD,∠CON=∠DON=$\frac{1}{2}$∠COB,
∴∠MON=∠BOM+∠DON=$\frac{1}{2}$(∠AOD+∠COB)=90°.
(3)
∵∠COD=50°,
∴∠AOB=2∠COD=100°,
∴∠COB=180°-100°=80°,∠AOD=180°-50°=130°,
∵OM为∠AOD的平分线,ON为∠COB的平分线,
∴∠AOM=$\frac{1}{2}$∠AOD=65°,
∠CON=$\frac{1}{2}$∠COB=40°,
∴∠MON=180°-∠AOM-∠CON=180°-65°-40°=75°.
(4)∠MON=$\frac{3}{2}$∠COD,理由如下:设∠COD=x,则∠AOB=2∠COD=2x,
∴∠AOD=180°-x,
∠COB=180°-2x,
∵OM为∠AOD的平分线,ON为∠COB的平分线,
∴∠AOM=$\frac{1}{2}$∠AOD=90°-\frac{1}{2}x,∠CON=$\frac{1}{2}$∠COB=90°-x,
∴∠MON
=180°-∠AOM-∠CON=180°-90°+\frac{1}{2}x=90°+\frac{3}{2}x=\frac{3}{2}∠COD.
查看更多完整答案,请扫码查看


