2025年1加1轻巧夺冠完美期末七年级数学上册人教版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末七年级数学上册人教版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
23. (13分)
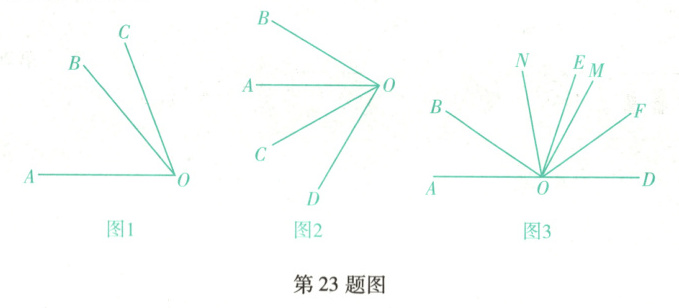
已知一个锐角,从这个角的顶点出发,在角的外部作一条射线,分别与这个角的两边组成两个角,若这两个角互为余角,则称该射线为“外邻余线”.例如,如图1,已知$\angle AOB(\angle AOB < 90^{\circ})$,射线$OC$在$\angle AOB$的外部,射线$OC$分别与$\angle AOB$的两边$OA$,$OB$所组成的两个角是$\angle AOC$和$\angle BOC$,若$\angle AOC$和$\angle BOC$互为余角,则称射线$OC$是$\angle AOB$的“外邻余线”.
(1)如图1,$\angle AOB = 50^{\circ}$,$OC$是$\angle AOB$的“外邻余线”,求$\angle BOC$的度数.
(2)如图2,$OC$是$\angle AOB$的“外邻余线”,$OD$是$\angle AOC$的“外邻余线”,且$\angle BOD = 90^{\circ}$,试判断$OA$,$OC$是否为$\angle BOD$的三等分线,并说明理由.
(3)如图3,点$A$,$O$,$D$在同一条直线上,$\angle AOB = \alpha(\alpha < 60^{\circ})$,$OE$平分$\angle BOD$,$OF$平分$\angle DOE$,$OM$和$ON$分别是$\angle DOF$和$\angle EOF$的“外邻余线”,求$\angle MON$的度数.(用含$\alpha$的代数式表示)
已知一个锐角,从这个角的顶点出发,在角的外部作一条射线,分别与这个角的两边组成两个角,若这两个角互为余角,则称该射线为“外邻余线”.例如,如图1,已知$\angle AOB(\angle AOB < 90^{\circ})$,射线$OC$在$\angle AOB$的外部,射线$OC$分别与$\angle AOB$的两边$OA$,$OB$所组成的两个角是$\angle AOC$和$\angle BOC$,若$\angle AOC$和$\angle BOC$互为余角,则称射线$OC$是$\angle AOB$的“外邻余线”.
(1)如图1,$\angle AOB = 50^{\circ}$,$OC$是$\angle AOB$的“外邻余线”,求$\angle BOC$的度数.
(2)如图2,$OC$是$\angle AOB$的“外邻余线”,$OD$是$\angle AOC$的“外邻余线”,且$\angle BOD = 90^{\circ}$,试判断$OA$,$OC$是否为$\angle BOD$的三等分线,并说明理由.
(3)如图3,点$A$,$O$,$D$在同一条直线上,$\angle AOB = \alpha(\alpha < 60^{\circ})$,$OE$平分$\angle BOD$,$OF$平分$\angle DOE$,$OM$和$ON$分别是$\angle DOF$和$\angle EOF$的“外邻余线”,求$\angle MON$的度数.(用含$\alpha$的代数式表示)

答案:
23.解:
(1)
∵$OC$是$\angle AOB$的外邻余线,
∴$\angle BOC + \angle AOC = 90^{\circ}$,
∴$2\angle BOC + \angle AOB = 90^{\circ}$,
∵$\angle AOB = 50^{\circ}$,
∴$\angle BOC = \frac{90^{\circ} - 50^{\circ}}{2} = 20^{\circ}$.
(2)$OA$,$OC$是$\angle BOD$的三等分线,理由如下:
∵$OC$是$\angle AOB$的“外邻余线”,
∴$\angle AOC + \angle BOC = 90^{\circ}$,
∵$\angle BOD = 90^{\circ}$,
∴$\angle DOC + \angle BOC = 90^{\circ}$,
∴$\angle AOC = \angle DOC$,同理可得$\angle AOB = \angle DOC$,
∴$\angle AOC = \angle DOC = \angle AOB$,
∴$OA$,$OC$是$\angle BOD$的三等分线.
(3)
∵$\angle AOB = \alpha (\alpha < 60^{\circ})$,
∴$\angle BOD = 180^{\circ} - \angle AOB = 180^{\circ} - \alpha$,
∵$OE$平分$\angle BOD$,
∴$\angle EOD = \frac{1}{2} \angle BOD = 90^{\circ} - \frac{\alpha}{2}$,
∵$OF$平分$\angle DOE$,
∴$\angle EOF = \angle FOD = \frac{1}{2} \angle EOD = 45^{\circ} - \frac{\alpha}{4}$,
∵$OM$是$\angle DOF$的“外邻余线”,
∴$\angle MOF + \angle MOD = 90^{\circ}$,
∴$2\angle MOF + \angle FOD = 90^{\circ}$,
∴$\angle MOF = 22.5^{\circ} + \frac{\alpha}{8}$,
∴$\angle EOM = \angle EOF - \angle MOF = 22.5^{\circ} - \frac{3\alpha}{8}$,
∵$ON$是$\angle EOF$的“外邻余线”,
∴$\angle NOE + \angle NOF = 90^{\circ}$,
∴$2\angle NOE + \angle EOF = 90^{\circ}$,
∴$\angle NOE = 22.5^{\circ} + \frac{\alpha}{8}$,
∴$\angle MON = \angle NOE + \angle EOM = 22.5^{\circ} + \frac{\alpha}{8} + 22.5^{\circ} - \frac{3\alpha}{8} = 45^{\circ} - \frac{\alpha}{4}$.
(1)
∵$OC$是$\angle AOB$的外邻余线,
∴$\angle BOC + \angle AOC = 90^{\circ}$,
∴$2\angle BOC + \angle AOB = 90^{\circ}$,
∵$\angle AOB = 50^{\circ}$,
∴$\angle BOC = \frac{90^{\circ} - 50^{\circ}}{2} = 20^{\circ}$.
(2)$OA$,$OC$是$\angle BOD$的三等分线,理由如下:
∵$OC$是$\angle AOB$的“外邻余线”,
∴$\angle AOC + \angle BOC = 90^{\circ}$,
∵$\angle BOD = 90^{\circ}$,
∴$\angle DOC + \angle BOC = 90^{\circ}$,
∴$\angle AOC = \angle DOC$,同理可得$\angle AOB = \angle DOC$,
∴$\angle AOC = \angle DOC = \angle AOB$,
∴$OA$,$OC$是$\angle BOD$的三等分线.
(3)
∵$\angle AOB = \alpha (\alpha < 60^{\circ})$,
∴$\angle BOD = 180^{\circ} - \angle AOB = 180^{\circ} - \alpha$,
∵$OE$平分$\angle BOD$,
∴$\angle EOD = \frac{1}{2} \angle BOD = 90^{\circ} - \frac{\alpha}{2}$,
∵$OF$平分$\angle DOE$,
∴$\angle EOF = \angle FOD = \frac{1}{2} \angle EOD = 45^{\circ} - \frac{\alpha}{4}$,
∵$OM$是$\angle DOF$的“外邻余线”,
∴$\angle MOF + \angle MOD = 90^{\circ}$,
∴$2\angle MOF + \angle FOD = 90^{\circ}$,
∴$\angle MOF = 22.5^{\circ} + \frac{\alpha}{8}$,
∴$\angle EOM = \angle EOF - \angle MOF = 22.5^{\circ} - \frac{3\alpha}{8}$,
∵$ON$是$\angle EOF$的“外邻余线”,
∴$\angle NOE + \angle NOF = 90^{\circ}$,
∴$2\angle NOE + \angle EOF = 90^{\circ}$,
∴$\angle NOE = 22.5^{\circ} + \frac{\alpha}{8}$,
∴$\angle MON = \angle NOE + \angle EOM = 22.5^{\circ} + \frac{\alpha}{8} + 22.5^{\circ} - \frac{3\alpha}{8} = 45^{\circ} - \frac{\alpha}{4}$.
查看更多完整答案,请扫码查看


