《2025年1加1轻巧夺冠完美期末七年级数学上册人教版辽宁专版》

22. (12 分)(抚顺顺城期末)
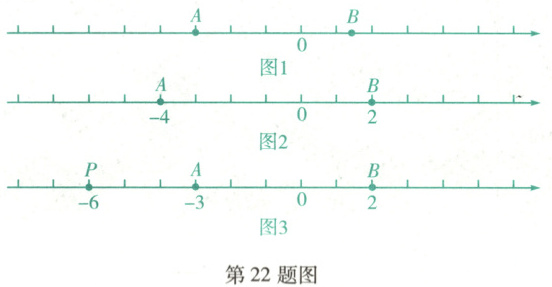
如图 1, $A$, $B$ 为数轴上不重合的两个点, $P$ 为数轴上任一点, 我们比较线段 $PA$ 和 $PB$ 的长度, 将较短线段的长度定义为点 $P$ 到线段 $AB$ 的“亲近距离”. 特别地, 若线段 $PA$ 和 $PB$ 的长度相等, 则将线段 $PA$ 或 $PB$ 的长度定义为点 $P$ 到线段 $AB$ 的“亲近距离”.
(1)如图 2, 点 $A$ 表示的数是 $-4$, 点 $B$ 表示的数是 2.
①若点 $P$ 表示的数是 $-3$, 求点 $P$ 到线段 $AB$ 的“亲近距离”.
②若点 $P$ 表示的数是 $m$, 点 $P$ 到线段 $AB$ 的“亲近距离”为 3, 求 $m$ 的值.
(2)如图 3, 在数轴上, 点 $P$ 表示的数是 $-6$, 点 $A$ 表示的数是 $-3$, 点 $B$ 表示的数是 2. 点 $P$ 以每秒 3 个单位长度的速度沿数轴向右运动, 同时点 $B$ 以每秒 1 个单位长度的速度沿数轴向右运动. 设运动的时间为 $t$ 秒, 当点 $P$ 到线段 $AB$ 的“亲近距离”为 2 时, 请直

接

写

出

$t$ 的值.

答案： 22.解：
(1)①
∵点A表示的数是 - 4，点B表示的数是2，若点P表示的数是 - 3，
∴PA = - 3 + 4 = 1，PB = 1 + 2 = 3，
∴点P到线段AB的“亲近距离”为1。
②
∵点A表示的数为 - 4，点B表示的数为2，
∴点P到线段AB的“亲近距离”为3时，分三种情况：I.当点P在点A的左侧时，PA ＜ PB，
∵点A到线段AB的“亲近距离”为3，有 - 4 - m = 3，解得m = - 7；II.当点P在点A和点B之间时，
∵PA = m + 4，PB = 2 - m，如果m + 4 = 3，解得m = - 1，如果2 - m = 3，解得m = - 1；III.当点P在点B的右侧时，PB ＜ PA，
∵点P到线段AB的“亲近距离”为3，有m - 2 = 3，解得m = 5。
综上所述，m的值为 - 7或 - 1或5。
(2)分四种情况：①当点P在点A的左侧且PA ＜ PB时，有 - 3 - (- 6 + 3t) = 2，解得t = $\frac{1}{3}$；②当点P在点A的右侧且PA ＜ PB时，有(- 6 + 3t) - (- 3) = 2，解得t = $\frac{5}{3}$；③当点P在点B的左侧且PB ＜ PA时，有2 + t - (- 6 + 3t) = 2，解得t = 3；④当点P在点B的右侧且PB ＜ PA时，有(- 6 + 3t) - (2 + t) = 2，解得t = 5。
综上所述，t的值为$\frac{1}{3}$或$\frac{5}{3}$或3或5。