2025年1加1轻巧夺冠完美期末七年级数学上册人教版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末七年级数学上册人教版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
20. (8 分)(大连中山期末)
综合与实践
【问题背景】
在小学, 我们知道像 12, 27, 36, 45, 108, …这样的自然数能被 3 整除. 一般地, 如果一个自然数的所有数位上的数字之和能被 3 整除, 那么这个自然数就能被 3 整除. 我们可以论证这个结论的正确性. 以三位数为例, 设 $\overline{abc}$ 是一个三位数, 若 $a + b + c$ 可以被 3 整除, 则这个数可以被 3 整除. 论证过程如下:
$\overline{abc} = 100a + 10b + c = (99a + 9b) + (a + b + c)$, 显然 $99a + 9b$ 能被 3 整除, 因此, 如果 $a + b + c$ 可以被 3 整除, 那么 $\overline{abc}$ 就能被 3 整除.
【拓展探究】
小聪在学习完课本上的数学活动后, 对数的整除很感兴趣, 于是自己研究了被 7 整除的数的特征, 先从两位数开始研究:
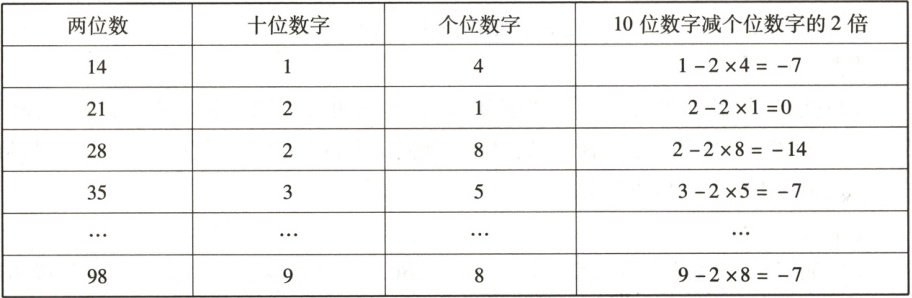
他发现如果一个两位数的十位数字减去个位数字的 2 倍得到的结果是 7 的倍数, 那么这个两位数就能被 7 整除.
(1)请你仿照问题背景中的代数推理方法验证小聪发现的结论.
(2)小聪继续探究发现他得到的结论可以推广到任意正整数: 假设该正整数的个位数字是 $b$, 除个位数字外的部分用 $a$ 表示, 推理过程与上面相同, 依然能得到当 $a - 2b$ 是 7 的倍数时, 原数能被 7 整除, 并且该结论反之亦成立. 请按照小聪推广后的结论解决下列问题:
①判断 7 938 是否能被 7 整除, 并写出判断过程.
②若一个正数 $m$ 能被 7 整除, $m$ 的最后四位数为 3 025, 求 $m$ 的最小值.
综合与实践
【问题背景】
在小学, 我们知道像 12, 27, 36, 45, 108, …这样的自然数能被 3 整除. 一般地, 如果一个自然数的所有数位上的数字之和能被 3 整除, 那么这个自然数就能被 3 整除. 我们可以论证这个结论的正确性. 以三位数为例, 设 $\overline{abc}$ 是一个三位数, 若 $a + b + c$ 可以被 3 整除, 则这个数可以被 3 整除. 论证过程如下:
$\overline{abc} = 100a + 10b + c = (99a + 9b) + (a + b + c)$, 显然 $99a + 9b$ 能被 3 整除, 因此, 如果 $a + b + c$ 可以被 3 整除, 那么 $\overline{abc}$ 就能被 3 整除.
【拓展探究】
小聪在学习完课本上的数学活动后, 对数的整除很感兴趣, 于是自己研究了被 7 整除的数的特征, 先从两位数开始研究:

他发现如果一个两位数的十位数字减去个位数字的 2 倍得到的结果是 7 的倍数, 那么这个两位数就能被 7 整除.
(1)请你仿照问题背景中的代数推理方法验证小聪发现的结论.
(2)小聪继续探究发现他得到的结论可以推广到任意正整数: 假设该正整数的个位数字是 $b$, 除个位数字外的部分用 $a$ 表示, 推理过程与上面相同, 依然能得到当 $a - 2b$ 是 7 的倍数时, 原数能被 7 整除, 并且该结论反之亦成立. 请按照小聪推广后的结论解决下列问题:
①判断 7 938 是否能被 7 整除, 并写出判断过程.
②若一个正数 $m$ 能被 7 整除, $m$ 的最后四位数为 3 025, 求 $m$ 的最小值.
答案:
20.解:
(1)$\overline{ab}$ = 7a + 7b + 3a - 6b = 7(a + b) + 3(a - 2b),显然7(a + b)能被7整除,因此,如果3(a - 2b)可以被7整除,那么$\overline{ab}$就能被7整除。
(2)①能,判断过程如下:7938的个位数字是8,除个位数字外的部分为793,因为793 - 2×8 = 777 = 7×111,所以7938能被7整除。
②由题意可知m的最小值为一个五位数,设m = $\overline{a3025}$,m的个位数字是5,除个位数字外的部分是$\overline{a302}$ = 1000a + 302,1000a + 302 - 5×2 = 1000a + 292,由题意易知当a = 1或2或3或4,均不符合题意,当a = 5时,1000×5 + 292 = 756×7,所以m的最小值为53025。
(1)$\overline{ab}$ = 7a + 7b + 3a - 6b = 7(a + b) + 3(a - 2b),显然7(a + b)能被7整除,因此,如果3(a - 2b)可以被7整除,那么$\overline{ab}$就能被7整除。
(2)①能,判断过程如下:7938的个位数字是8,除个位数字外的部分为793,因为793 - 2×8 = 777 = 7×111,所以7938能被7整除。
②由题意可知m的最小值为一个五位数,设m = $\overline{a3025}$,m的个位数字是5,除个位数字外的部分是$\overline{a302}$ = 1000a + 302,1000a + 302 - 5×2 = 1000a + 292,由题意易知当a = 1或2或3或4,均不符合题意,当a = 5时,1000×5 + 292 = 756×7,所以m的最小值为53025。
查看更多完整答案,请扫码查看


