2025年1加1轻巧夺冠完美期末七年级数学上册人教版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末七年级数学上册人教版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. (抚顺新宾期末)如图,$O$是直线$AB$上一点,过点$O$作任意射线$OM$,$OC$平分$\angle AOM$,$OD$平分$\angle BOM$,则$\angle COD$的度数是(
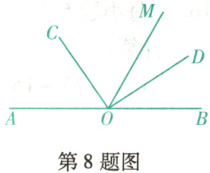
A.$80^{\circ}$
B.$90^{\circ}$
C.$100^{\circ}$
D.不能确定
B
)
A.$80^{\circ}$
B.$90^{\circ}$
C.$100^{\circ}$
D.不能确定
答案:
8.B
9. (盘锦盘山期末)下列图形中所标识的角,能同时用$\angle AOB$,$\angle O$,$\angle 1$三种方法表示的是(
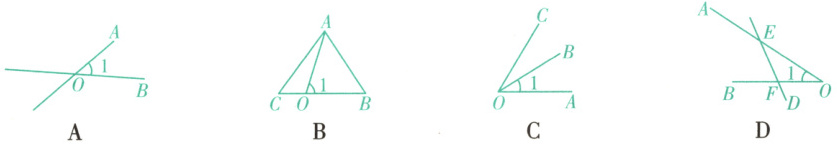
D
)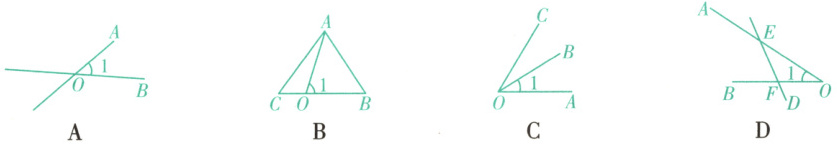
答案:
9.D
10. (大连金州期末)用边长相等的正方形和等边三角形卡片按如图所示的方式和规律拼出图形.拼第1个图形所用两种卡片的总数为7枚,拼第2个图形所用两种卡片的总数为12枚……若按照这样的规律拼出的第$n$个图形中,所用正方形卡片比等边三角形卡片多10枚,则拼第$n$个图形所用两种卡片的总数为(

A.57枚
B.52枚
C.50枚
D.47枚
B
)
A.57枚
B.52枚
C.50枚
D.47枚
答案:
10.B 【解析】
∵第1个图形中有正方形和等边三角形卡片2+5×1=7(枚),所用正方形卡片比等边三角形卡片多1枚,第2个图形中有正方形和等边三角形卡片2+5×2=12(枚),所用正方形卡片比等边三角形卡片多2枚,第3个图形中有正方形和等边三角形卡片2+5×3=17(枚),所用正方形卡片比等边三角形卡片多3枚,
∴第4个图形中有正方形和等边三角形卡片2+5×4=22(枚),所用正方形卡片比等边三角形卡片多4枚,⋯,第n个图形中有正方形和等边三角形卡片(2+5n)枚,所用正方形卡片比等边三角形卡片多n枚,
∵第n个图形中,所用正方形卡片比等边三角形卡片多10枚,
∴n=10,当n=10时,2+5n=2+5×10=52,
∴第n个图形所用两种卡片的总数为52枚.
∵第1个图形中有正方形和等边三角形卡片2+5×1=7(枚),所用正方形卡片比等边三角形卡片多1枚,第2个图形中有正方形和等边三角形卡片2+5×2=12(枚),所用正方形卡片比等边三角形卡片多2枚,第3个图形中有正方形和等边三角形卡片2+5×3=17(枚),所用正方形卡片比等边三角形卡片多3枚,
∴第4个图形中有正方形和等边三角形卡片2+5×4=22(枚),所用正方形卡片比等边三角形卡片多4枚,⋯,第n个图形中有正方形和等边三角形卡片(2+5n)枚,所用正方形卡片比等边三角形卡片多n枚,
∵第n个图形中,所用正方形卡片比等边三角形卡片多10枚,
∴n=10,当n=10时,2+5n=2+5×10=52,
∴第n个图形所用两种卡片的总数为52枚.
11. (大连金普期末)圆周率$\pi = 3.1415926·s$,用四舍五入法把$\pi$精确到0.01,得到的近似值是
3.14
。
答案:
11.3.14
12. (营口期末)在$-(-2)$,$-3^{2}$,$-|-4|$,$-\frac{2^{2}}{5}$,$(-1)^{2025}$中,负数共有
4
个。
答案:
12.4
13. (大连沙河口期末)一个角的度数是$70^{\circ}45'$,那么这个角的余角的度数是
19°15′
。
答案:
13.19°15′
14. (抚顺县期末)如图是两个正方形组成的图形(不重叠无缝隙),用含字母$a$的整式表示出阴影部分的面积为
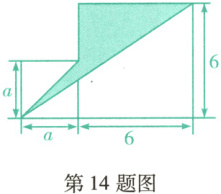
$\frac{1}{2}a^{2}-3a+18$
。
答案:
14.$\frac{1}{2}a^{2}-3a+18$【解析】阴影部分的面积=$a^{2}+6^{2}-\frac{1}{2}a^{2}-\frac{1}{2}(a+6)×6=a^{2}+36-\frac{1}{2}a^{2}-3a-18=\frac{1}{2}a^{2}-3a+18$.
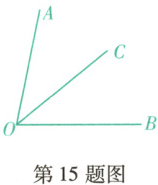
15. (抚顺望花期末)如图,$\angle AOB = 80^{\circ}$,$OC$平分$\angle AOB$.若$\angle BOD = 20^{\circ}$,则$\angle COD$的度数为
20°或60°
。
答案:
15.20°或60°【解析】
∵∠AOB=80°,OC平分∠AOB,
∴∠BOC=$\frac{1}{2}$∠AOB=40°,若∠BOD=20°,分两种情况:①当OD在∠BOC的内部时
∠COD=∠BOC-∠BOD=40°-20°=20°;
②当OD在∠BOC的外部时,∠COD=∠BOC+∠BOD=40°+20°=60°.综上所述,∠COD的度数为20°或60°.
∵∠AOB=80°,OC平分∠AOB,
∴∠BOC=$\frac{1}{2}$∠AOB=40°,若∠BOD=20°,分两种情况:①当OD在∠BOC的内部时
∠COD=∠BOC-∠BOD=40°-20°=20°;
②当OD在∠BOC的外部时,∠COD=∠BOC+∠BOD=40°+20°=60°.综上所述,∠COD的度数为20°或60°.
查看更多完整答案,请扫码查看


