第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
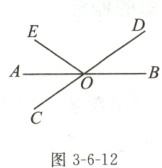
例4 如图3 - 6 - 12,直线$AB$,$CD$相交于点$O$,$OA$平分$\angle EOC$。
(1)若$\angle EOC = 70^{\circ}$,求$\angle BOD$的度数;
(2)若$\angle EOC:\angle EOD = 2:3$,求$\angle BOD$的度数。
(1)若$\angle EOC = 70^{\circ}$,求$\angle BOD$的度数;
(2)若$\angle EOC:\angle EOD = 2:3$,求$\angle BOD$的度数。

答案:
1. (1)
解:
因为$OA$平分$\angle EOC$,$\angle EOC = 70^{\circ}$,根据角平分线的定义:若$OA$平分$\angle EOC$,则$\angle AOC=\frac{1}{2}\angle EOC$。
所以$\angle AOC=\frac{1}{2}×70^{\circ}=35^{\circ}$。
又因为$\angle BOD$与$\angle AOC$是对顶角,根据对顶角的性质:对顶角相等,即$\angle BOD = \angle AOC$。
所以$\angle BOD = 35^{\circ}$。
2. (2)
解:
因为$\angle EOC+\angle EOD = 180^{\circ}$(邻补角的定义:两角之和为$180^{\circ}$),且$\angle EOC:\angle EOD = 2:3$。
设$\angle EOC = 2x$,$\angle EOD = 3x$,则$2x + 3x=180^{\circ}$。
合并同类项得$5x = 180^{\circ}$,解得$x = 36^{\circ}$。
所以$\angle EOC=2x = 72^{\circ}$。
因为$OA$平分$\angle EOC$,根据角平分线的定义$\angle AOC=\frac{1}{2}\angle EOC$。
所以$\angle AOC=\frac{1}{2}×72^{\circ}=36^{\circ}$。
又因为$\angle BOD$与$\angle AOC$是对顶角(对顶角相等),所以$\angle BOD=\angle AOC = 36^{\circ}$。
综上,(1)$\angle BOD = 35^{\circ}$;(2)$\angle BOD = 36^{\circ}$。
解:
因为$OA$平分$\angle EOC$,$\angle EOC = 70^{\circ}$,根据角平分线的定义:若$OA$平分$\angle EOC$,则$\angle AOC=\frac{1}{2}\angle EOC$。
所以$\angle AOC=\frac{1}{2}×70^{\circ}=35^{\circ}$。
又因为$\angle BOD$与$\angle AOC$是对顶角,根据对顶角的性质:对顶角相等,即$\angle BOD = \angle AOC$。
所以$\angle BOD = 35^{\circ}$。
2. (2)
解:
因为$\angle EOC+\angle EOD = 180^{\circ}$(邻补角的定义:两角之和为$180^{\circ}$),且$\angle EOC:\angle EOD = 2:3$。
设$\angle EOC = 2x$,$\angle EOD = 3x$,则$2x + 3x=180^{\circ}$。
合并同类项得$5x = 180^{\circ}$,解得$x = 36^{\circ}$。
所以$\angle EOC=2x = 72^{\circ}$。
因为$OA$平分$\angle EOC$,根据角平分线的定义$\angle AOC=\frac{1}{2}\angle EOC$。
所以$\angle AOC=\frac{1}{2}×72^{\circ}=36^{\circ}$。
又因为$\angle BOD$与$\angle AOC$是对顶角(对顶角相等),所以$\angle BOD=\angle AOC = 36^{\circ}$。
综上,(1)$\angle BOD = 35^{\circ}$;(2)$\angle BOD = 36^{\circ}$。
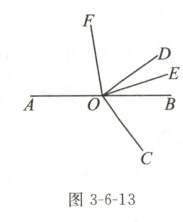
例5 如图3 - 6 - 13,$O$为直线$AB$上的一点,且$\angle COD$为直角,$OE$平分$\angle BOD$,$OF$平分$\angle AOE$,若$\angle BOC = 54^{\circ}$,求$\angle COE$和$\angle DOF$的度数。

答案:
例5 解:因为∠COD=90°,∠BOC = 54°
所以∠BOD=∠COD−∠BOC=90°−54°=36°.
因为OE平分∠BOD,
所以∠DOE=∠BOE=$\frac{1}{2}$∠BOD=18°,
所以∠COE=∠BOC+∠BOE=54°+18°=72°,∠AOE=180°−∠BOE=180°−18°=162°.
因为OF平分∠AOE,
所以∠EOF=$\frac{1}{2}$∠AOE=81°,
所以∠DOF=∠EOF−∠DOE=81°−18°=63°
所以∠BOD=∠COD−∠BOC=90°−54°=36°.
因为OE平分∠BOD,
所以∠DOE=∠BOE=$\frac{1}{2}$∠BOD=18°,
所以∠COE=∠BOC+∠BOE=54°+18°=72°,∠AOE=180°−∠BOE=180°−18°=162°.
因为OF平分∠AOE,
所以∠EOF=$\frac{1}{2}$∠AOE=81°,
所以∠DOF=∠EOF−∠DOE=81°−18°=63°
1. 如图3 - 6 - 14,在$\angle AOB$内部任取一点$C$,作射线$OC$,则下列结论一定成立的是(
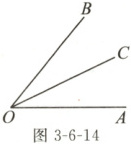
A.$\angle AOC > \angle BOC$
B.$\angle BOC < \angle AOB$
C.$\angle AOC < \angle BOC$
D.$\angle BOC > \angle AOB$
B
)
A.$\angle AOC > \angle BOC$
B.$\angle BOC < \angle AOB$
C.$\angle AOC < \angle BOC$
D.$\angle BOC > \angle AOB$
答案:
1.B
2. 如图3 - 6 - 15,点$O$在直线$AB$上,射线$OC$平分$\angle DOB$。若$\angle COB = 25^{\circ}$,则$\angle AOD$等于(
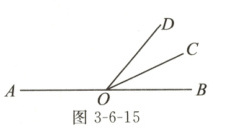
A.$25^{\circ}$
B.$50^{\circ}$
C.$130^{\circ}$
D.$155^{\circ}$
C
)
A.$25^{\circ}$
B.$50^{\circ}$
C.$130^{\circ}$
D.$155^{\circ}$
答案:
2.C
3. 若$\angle 1 = 40.4^{\circ}$,$\angle 2 = 40^{\circ}4'$,则$\angle 1$与$\angle 2$的大小关系是(
A.$\angle 1 = \angle 2$
B.$\angle 1 > \angle 2$
C.$\angle 1 < \angle 2$
D.以上都不对
B
)A.$\angle 1 = \angle 2$
B.$\angle 1 > \angle 2$
C.$\angle 1 < \angle 2$
D.以上都不对
答案:
3.B
4. (1)如图3 - 6 - 16,过直线$AB$上一点$O$作射线$OC$,使$\angle BOC = 29^{\circ}18'$,则$\angle AOC$的度数为
(2)计算:$28.3^{\circ} - 26^{\circ}34' =$
(3)计算:$23.5^{\circ} + 12^{\circ}30' =$
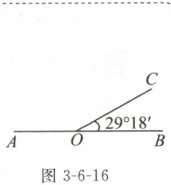
150°42′
;(2)计算:$28.3^{\circ} - 26^{\circ}34' =$
1
$^{\circ}$44
$' $;(3)计算:$23.5^{\circ} + 12^{\circ}30' =$
36
$^{\circ}$。
答案:
4.
(1)150°42′
(2)1 44
(3)36
(1)150°42′
(2)1 44
(3)36
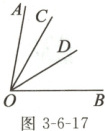
5. 如图3 - 6 - 17所示,$\angle AOB = 80^{\circ}$,$\angle AOC = 20^{\circ}$,$OD$是$\angle BOC$的平分线,求$\angle BOD$的度数。

答案:
5.解:由题意,得∠BOC=∠AOB−∠AOC=
80°−20°=60°.
因为OD是∠BOC的平分线,
所以∠BOD=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×60°=30°.
80°−20°=60°.
因为OD是∠BOC的平分线,
所以∠BOD=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×60°=30°.
查看更多完整答案,请扫码查看


