《2025年全品学练考七年级数学上册华师大版》

我们已经用直尺和圆规按一定步骤解决了作一条线段等于已知线段和作一个角等于已知角这两个作图问题。人们将利用没有刻度的直尺和圆规这两种工具作几何图形的方法称为“尺规作图”。

答案： 没有刻度

例2 如图3 - 6 - 10，已知$\angle AOB$，求作一个角，使它等于$2\angle AOB$。

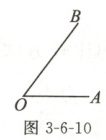
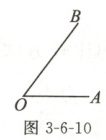
答案：
　

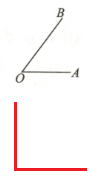
例3（教材补充例题）计算：
（1）$34^{\circ}34' + 21^{\circ}51'$； （2）$180^{\circ} - 52^{\circ}31'$；
（3）$153^{\circ}19'42'' + 26^{\circ}40'18''$； （4）$180^{\circ} - (34^{\circ}54' + 21^{\circ}33')$。

答案： 例3　
(1)56°25′　
(2)127°29′
(3)180°　
(4)123°33′　　　　　　　　　　　　

1. 在一张纸上画出一个角$\angle AOC$并剪下（如图3 - 6 - 11），将这个角对折，折痕为射线$OB$。想想看，折痕$OB$与角两边所成的两个角的大小有什么关系？

答案： 1.解:折痕OB与角两边所成的两个角∠AOB 与∠BOC大小相等.

2. 如图3 - 6 - 11，符号语言：因为$OB$平分$\angle AOC$，所以∠AOB = ∠BOC = $\frac{1}{2}\angle AOC$或$\angle AOC = 2$∠AOB = $2$∠BOC。

答案： 2.∠AOB　∠BOC　∠AOB　∠BOC

角的平分线
从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线。

答案： 相等