《2025年全品学练考七年级数学上册华师大版》

1. 已知 M 是线段 AB 的中点，下列式子：① AB = 2AM；② $ BM = \frac{1}{2}AB $；③ AM = BM；④ AM + BM = AB 中，正确的有 (D)

A.1 个
B.2 个
C.3 个
D.4 个

答案： 1.D

2. 如图 3 - 5 - 19，点 C，D 在线段 AB 上，AC = BD. 若 AD = 8 cm，则 BC = 8 cm.

答案： 2.8

3. 看图填空(如图 3 - 5 - 20)：
(1)AC = BD - CD + AB；
(2)AD - AB = AC - AB + CD；
(3)若线段 AD = 5 cm，线段 AB = 1.8 cm，线段 CD = 1.8 cm，则线段 BC = 1.4 cm；
(4)如果线段 AD = 5 cm，线段 AB = 2 cm，C 是 BD 的中点，那么线段 AC = 3.5 cm.

答案： 3.
(1)CD
(2)AB
(3)1.4
(4)3.5

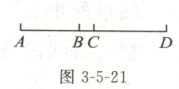
4. 如图 3 - 5 - 21，B，C 为线段 AD 上的两点，C 为线段 AD 的中点，AC = 5 cm，BD = 6 cm，求线段 AB 的长度.

答案： 4.4cm

1. 角的概念
①角是由两条有公共端点的射线组成的图形；②角可以看成是由一条射线绕着它的端点旋转而成的图形.射线的端点叫做角的顶点，起始位置的射线叫做角的始边，终止位置的射线叫做角的终边.
2. 角的表示方法

角可以用几种不同的方法表示：
(1)用三个大写英文字母表示角时，表示角的顶点的字母必须写在中间.如图3-6-1①，记作∠AOB.
(2)用一个大写英文字母表示角(角的顶点处只有一个角).如图②，记作∠O.
(3)用一个阿拉伯数字或希腊字母(α，β，γ)表示角时，应在角的顶点附近画一个小括弧，再标注上阿拉伯数字或希腊字母.如图③，记作1；如图④，记作∠α.
3. 我们用旋转的观点来研究角，当一条射线绕着它的端点旋转时角逐渐由小变大，依次形成锐角、直角、钝角、平角、周角，请看下表：

答案： 1. ①公共端点 射线 ②旋转 顶点 始边 终边 2.
(1)∠AOB
(2)∠O
(3)1 ∠α 3. 锐角 直角 钝角 平角 周角 0° 90° 90° 180° 180° 360°