第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
初识新知
(1)圆是由
(2)由
(1)圆是由
曲线
围成的封闭图形;(2)由
线段
围成的封闭图形叫做多边形,按照组成多边形的边的条数,多边形可分为三角形(三边形)、四边形、五边形、六边形……
答案:
(1)曲线
(2)线段
(1)曲线
(2)线段
例 (教材补充例题)如图 3 - 4 - 1 所示的图形中多边形是

(2)(3)(6)(8)
(填序号),它们的名称分别为图(2)是四边形,图(3)是七边形,图(6)是五边形,图(8)是七边形
.
答案:
例
(2)
(3)
(6)
(8) 图
(2)是四边形,图
(3)是七边形,图
(6)是五边形,图
(8)是七边形
(2)
(3)
(6)
(8) 图
(2)是四边形,图
(3)是七边形,图
(6)是五边形,图
(8)是七边形
在多边形中,三角形是最基本的图形,我们可以将多边形分割为若干个三角形,从而将多边形转化为三角形的问题进行研究:
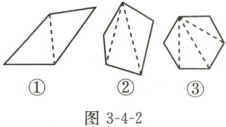
(1)如图 3 - 4 - 2 中,分别从多边形一个顶点出发引对角线,可将多边形分别分成几个三角形?从$n$边形的一个顶点出发,引对角线可将$n$边形分成几个三角形?
(2)若分别从四边形、五边形、六边形及$n$边形边上的任意一点(顶点除外)出发与各顶点连线可将多边形分别分成几个三角形?
(3)若从上述多边形内任意一点出发与各顶点连线可将多边形分成几个三角形?
(1)如图 3 - 4 - 2 中,分别从多边形一个顶点出发引对角线,可将多边形分别分成几个三角形?从$n$边形的一个顶点出发,引对角线可将$n$边形分成几个三角形?
(2)若分别从四边形、五边形、六边形及$n$边形边上的任意一点(顶点除外)出发与各顶点连线可将多边形分别分成几个三角形?
(3)若从上述多边形内任意一点出发与各顶点连线可将多边形分成几个三角形?

答案:
解:
(1)从四边形的一个顶点出发,引对角线可将四边形分成2个三角形;从五边形的一个顶点出发,引对角线可将五边形分成3个三角形;从六边形的一个顶点出发,引对角线可将六边形分成4个三角形;从n边形的一个顶点出发,引对角线可将n边形分成(n−2)个三角形.
(2)如图①,从四边形一边上一点出发与各顶点连线可将其分割成3个三角形;从五边形一边上一点出发与各顶点连线可将其分割成4个三角形;从六边形一边上一点出发与各顶点连线可将其分割成5个三角形;从n边形一边上一点出发与各顶点连线可将其分割成(n−1)个三角形.
(3)如图②,从四边形内一点出发与各顶点连线可将其分割为4个三角形;从五边形内一点出发与各顶点连线可将其分割为5个三角形;从六边形内一点出发与各顶点连线可将其分割为6个三角形;从n边形内一点出发与各顶点连线可将其分割为n个三角形.
(1)从四边形的一个顶点出发,引对角线可将四边形分成2个三角形;从五边形的一个顶点出发,引对角线可将五边形分成3个三角形;从六边形的一个顶点出发,引对角线可将六边形分成4个三角形;从n边形的一个顶点出发,引对角线可将n边形分成(n−2)个三角形.
(2)如图①,从四边形一边上一点出发与各顶点连线可将其分割成3个三角形;从五边形一边上一点出发与各顶点连线可将其分割成4个三角形;从六边形一边上一点出发与各顶点连线可将其分割成5个三角形;从n边形一边上一点出发与各顶点连线可将其分割成(n−1)个三角形.
(3)如图②,从四边形内一点出发与各顶点连线可将其分割为4个三角形;从五边形内一点出发与各顶点连线可将其分割为5个三角形;从六边形内一点出发与各顶点连线可将其分割为6个三角形;从n边形内一点出发与各顶点连线可将其分割为n个三角形.
巧 归纳
1. 从$n$边形一个顶点出发,引对角线可将$n$边形分成
2. 从$n$边形边上的任意一点(非顶点)出发,与各顶点连线可将$n$边形分成
3. 从$n$边形内任意一点出发,与各顶点连线可将$n$边形分成
1. 从$n$边形一个顶点出发,引对角线可将$n$边形分成
(n−2)
个三角形.2. 从$n$边形边上的任意一点(非顶点)出发,与各顶点连线可将$n$边形分成
(n−1)
个三角形.3. 从$n$边形内任意一点出发,与各顶点连线可将$n$边形分成
n
个三角形.
答案:
1.(n−2) 2.(n−1) 3.n
1. 如图 3 - 4 - 3 所示的图形中,是四边形的是 (

A.①③
B.②③④
C.③④
D.①②④⑤
B
)
A.①③
B.②③④
C.③④
D.①②④⑤
答案:
1.B
2. 写出图 3 - 4 - 4 中平面图形的名称.
(1)
(4)
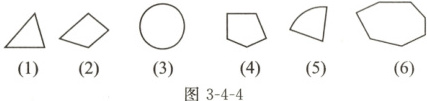
(1)
三角形
;(2)四边形
;(3)圆
;(4)
五边形
;(5)扇形
;(6)七边形
.
答案:
2.
(1)三角形
(2)四边形
(3)圆
(4)五边形
(5)扇形
(6)七边形
(1)三角形
(2)四边形
(3)圆
(4)五边形
(5)扇形
(6)七边形
查看更多完整答案,请扫码查看


