第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 列代数式:
(1) 若三角形的三条边长分别为 $ a $,$ b $,$ c $,则这个三角形的周长为
(2) 某班有男生 $ x $ 人,女生 21 人,这个班的学生一共有
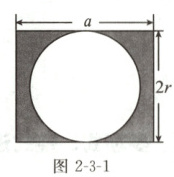
(3) 图 2 - 3 - 1 中阴影部分的面积为
(1) 若三角形的三条边长分别为 $ a $,$ b $,$ c $,则这个三角形的周长为
a+b+c
;(2) 某班有男生 $ x $ 人,女生 21 人,这个班的学生一共有
x+21
人;(3) 图 2 - 3 - 1 中阴影部分的面积为
2ar−πr²
。
答案:
1.
(1)a+b+c
(2)(x+21)
(3)2ar−πr²
(1)a+b+c
(2)(x+21)
(3)2ar−πr²
2. 第 1 题中列出的这些代数式有什么共同特点?它们与单项式有什么联系?
答案:
2.解:第1题中列出的这些代数式都是和或差的形式,可以看作是由几个单项式相加而成的.
多项式
定义:几个
多项式的项:在一个多项式中,每个
多项式的次数:多项式中,
整式:
定义:几个
单项式
的和叫做多项式。多项式的项:在一个多项式中,每个
单项式
叫做多项式的项。因为把多项式视为“和”的形式,所以多项式中的各项包括前面的正负号。多项式中不含字母
的项叫做常数项。多项式的次数:多项式中,
次数最高项
的次数,就是这个多项式的次数。整式:
单项式
与多项式
统称为整式。
答案:
单项式 单项式 字母 次数最高项 单项式 多项式
例 1(教材典题)指出下列多项式的项和次数:
(1) $ a^{3}-a^{2}b + ab^{2}-b^{3} $; (2) $ 3n^{4}-2n^{2}+1 $。
(1) $ a^{3}-a^{2}b + ab^{2}-b^{3} $; (2) $ 3n^{4}-2n^{2}+1 $。
答案:
例1 解:
(1)多项式a³−a²b+ab²−b³的项有a³,−a²b,ab²,−b³,次数是3.
(2)多项式3n⁴−2n²+1的项有3n⁴,−2n²,1,次数是4.
(1)多项式a³−a²b+ab²−b³的项有a³,−a²b,ab²,−b³,次数是3.
(2)多项式3n⁴−2n²+1的项有3n⁴,−2n²,1,次数是4.
变式 如果多项式 $ 6a^{m}-(n - 2)a + 4 $ 是关于 $ a $ 的二次二项式,$ m + 2n = $
6
。
答案:
变式 6
查看更多完整答案,请扫码查看


