第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
变式1 用“$>$”号或“$<$”号填空.
(1)$-(+1\dfrac{2}{3})$
(3)$-|-1|$
(1)$-(+1\dfrac{2}{3})$
<
$0$; (2)$+(-\dfrac{1}{4})$<
$-(-0.75)$;(3)$-|-1|$
<
$-(-1)$; (4)$-|-\dfrac{1}{3}|$<
$-[-(-\dfrac{1}{4})]$.
答案:
(1)$<$
(2)$<$
(3)$<$
(4)$<$
(1)$<$
(2)$<$
(3)$<$
(4)$<$
变式2 已知$a$,$b$为有理数,且$a<0$,$b>0$,$|b|<|a|$,则$a$,$b$,$-a$,$-b$的大小关系是(
A.$-b < a < b < -a$
B.$-b < b < -a < a$
C.$a < -b < b < -a$
D.$-a < b < -b < a$
C
)A.$-b < a < b < -a$
B.$-b < b < -a < a$
C.$a < -b < b < -a$
D.$-a < b < -b < a$
答案:
C
例3(教材补充例题)将下列各数在数轴上表示出来,并用“$<$”号连接起来:$-2\dfrac{1}{2}$,$-2$,$0$,$3$,$-1$,$-3\dfrac{1}{2}$,$1$.
答案:
解:在数轴上表示各数如图:
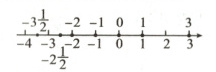
$-3\frac{1}{2} < -2 < -\frac{1}{2} < -2 < -1 < 0 < 1 < 3$.
解:在数轴上表示各数如图:

$-3\frac{1}{2} < -2 < -\frac{1}{2} < -2 < -1 < 0 < 1 < 3$.
变式 数学活动课上,小明设计如下表格并提出了如下问题,请同学们解答小明提出的问题:
将表格中的数化简后写在横线上,并画数轴,将横线上的结果在数轴上表示出来.

将表格中的数化简后写在横线上,并画数轴,将横线上的结果在数轴上表示出来.

答案:
解:如下表:

$-(+3.5)$ $(-1)^7$ $-0.5$的倒数 $+|-2.5|$ 比$-1$大$\frac{5}{2}$的数
$-3.5$ $-1$ $-2$ $2.5$ $\frac{3}{2}$
把各数在数轴上表示如图:
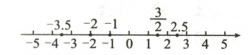
解:如下表:

$-(+3.5)$ $(-1)^7$ $-0.5$的倒数 $+|-2.5|$ 比$-1$大$\frac{5}{2}$的数
$-3.5$ $-1$ $-2$ $2.5$ $\frac{3}{2}$
把各数在数轴上表示如图:

1. 下列各数中,比$-2$小的数是(
A.$-1$
B.$2$
C.$-7$
D.$0$
C
)A.$-1$
B.$2$
C.$-7$
D.$0$
答案:
1 C
2. 下列各式中不正确的是(
A.$|-4|=-(-4)$
B.$|-5|<6$
C.$|-7|>|-2|$
D.$-8>-7$
D
)A.$|-4|=-(-4)$
B.$|-5|<6$
C.$|-7|>|-2|$
D.$-8>-7$
答案:
2 D
3. 比较大小:
(1)$-\dfrac{2}{3}$
(3)$|-3|$
(1)$-\dfrac{2}{3}$
>
$-\dfrac{3}{4}$;(2)$-\dfrac{1}{3}$<
$-0.3$;(3)$|-3|$
=
$-(-3)$;(4)$-|-\dfrac{1}{3}|$<
$|-\dfrac{1}{4}|$.
答案:
3
(1)$>$
(2)$<$
(3)$=$
(4)$>$
(1)$>$
(2)$<$
(3)$=$
(4)$>$
查看更多完整答案,请扫码查看


