第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
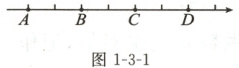
例2 如图1-3-1所示,已知$A$,$B$,$C$,$D$四个点在一条没有标明原点的数轴上。
(1)若点$A$和点$C$表示的数互为相反数,则原点为
(2)若点$B$和点$D$表示的数互为相反数,则原点为
(3)若点$A$和点$D$表示的数互为相反数,则在数轴上表示出原点$O$的位置。
(1)若点$A$和点$C$表示的数互为相反数,则原点为
B
;(2)若点$B$和点$D$表示的数互为相反数,则原点为
C
;(3)若点$A$和点$D$表示的数互为相反数,则在数轴上表示出原点$O$的位置。

答案:
(1)B
(2)C
(3)如图所示:
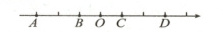
(1)B
(2)C
(3)如图所示:
在一个数的前面添上“$+$”号,仍表示这个数本身,所以与原数
相等
;在一个数的前面添上“$-$”号,表示这个数的相反数。即$-a$表示a
的相反数。
答案:
相等 a
例3 化简:
(1)$-(+10)$; (2)$+(-0.15)$; (3)$+(+3)$; (4)$-(-20)$。
(1)$-(+10)$; (2)$+(-0.15)$; (3)$+(+3)$; (4)$-(-20)$。
答案:
(1)-10;(2)-0.15;(3)3;(4)-(-20)
1. $-3$的相反数是(
A.$-3$
B.$3$
C.$-\frac{1}{3}$
D.$\frac{1}{3}$
B
)A.$-3$
B.$3$
C.$-\frac{1}{3}$
D.$\frac{1}{3}$
答案:
1.B
2. (教材典题)下列说法是否正确?为什么?
(1)正负号相反的两个数称互为相反数;
(2)相反数和我们以前学过的倒数是一样的;
(3)一个数的相反数的相反数等于这个数本身。
(1)正负号相反的两个数称互为相反数;
(2)相反数和我们以前学过的倒数是一样的;
(3)一个数的相反数的相反数等于这个数本身。
答案:
2.(1)错误,理由:只有正负号不同的两个数才称互为相反数,原说法错误.
(2)错误.理由:乘积是1的两个数互为倒数,与相反数不一样.
(3)正确.
(2)错误.理由:乘积是1的两个数互为倒数,与相反数不一样.
(3)正确.
3. 化简:
(1)$-(+22)$; (2)$+(-\frac{3}{5})$;
(3)$-[-(-3\frac{2}{5})]$。
(1)$-(+22)$; (2)$+(-\frac{3}{5})$;
(3)$-[-(-3\frac{2}{5})]$。
答案:
3.(1)-22;$(2)-\frac{3}{5};$$(3)-3\frac{2}{5}$
查看更多完整答案,请扫码查看


