《2026年高中必刷题高中数学必修第二册人教版》

19. [全国新课标Ⅱ2024·7,5 分]已知正三棱台$ABC - A_{1}B_{1}C_{1}$的体积为$\frac{52}{3}$,$AB = 6$,$A_{1}B_{1} = 2$,则$A_{1}A$与平面$ABC$所成角的正切值为(B)

A.$\frac{1}{2}$
B.1
C.2
D.3

答案：
19.B [解析]设正三棱台$ABC - A_{1}B_{1}C_{1}$的高为$h$。$\because AB = 6$，$A_{1}B_{1}=2$，$\therefore S_{\triangle ABC}=\frac{1}{2}×6×6×\sin\frac{\pi}{3}=9\sqrt{3}$，$S_{\triangle A_{1}B_{1}C_{1}}=\frac{1}{2}×2×2×\sin\frac{\pi}{3}=\sqrt{3}$。$\because$正三棱台$ABC - A_{1}B_{1}C_{1}$的体积$V=\frac{1}{3}(S_{\triangle ABC}+S_{\triangle A_{1}B_{1}C_{1}}+\sqrt{S_{\triangle ABC}· S_{\triangle A_{1}B_{1}C_{1}}})h=\frac{1}{3}(9\sqrt{3}+\sqrt{3}+\sqrt{9\sqrt{3}×\sqrt{3}})h=\frac{13\sqrt{3}}{3}h=\frac{52}{3}$，$\therefore h=\frac{4\sqrt{3}}{3}$。
如图，设$\triangle ABC$和$\triangle A_{1}B_{1}C_{1}$的中心分别为$O_{1},O$，连接$A_{1}O_{1}$，$O_{1}O$，$AO_{1}$，作$A_{1}D\perp$平面$ABC$交平面$ABC$于点$D$，由几何体$ABC - A_{1}B_{1}C_{1}$为正三棱台可知，点$D$在$AO_{1}$上，且四边形$A_{1}O_{1}OD$为矩形，其中$\angle A_{1}AD$即为直线$A_{1}A$与平面$ABC$所成的角。由$AB = 6$，$A_{1}B_{1}=2$，可得$OA = 2\sqrt{3}$，$O_{1}A_{1}=\frac{2\sqrt{3}}{3}$，
→悟：边长为$a$的正三角形的中心到各顶点的距离为$\frac{\sqrt{3}}{3}a$
$\therefore AD = OA - OD = OA - O_{1}A_{1}=\frac{4\sqrt{3}}{3}$，$\therefore\tan\angle A_{1}AD=\frac{A_{1}D}{AD}=\frac{\frac{4\sqrt{3}}{3}}{\frac{4\sqrt{3}}{3}}=1$。故选B．

20. [全国乙理 2023·9,5 分]已知$\triangle ABC$为等腰直角三角形,$AB$为斜边,$\triangle ABD$为等边三角形.若二面角$C - AB - D$为$150^{\circ}$,则直线$CD$与平面$ABC$所成角的正切值为(C)

A.$\frac{1}{5}$
B.$\frac{\sqrt{2}}{5}$
C.$\frac{\sqrt{3}}{5}$
D.$\frac{2}{5}$

答案：
20.C [解析]如图，设$AB$的中点为$O$，连接$CO,DO$，则$CO\perp AB$，$DO\perp AB$，于是$\angle COD$即为二面角$C - AB - D$的平面角。过点$D$作$DE\perp$平面$ABC$，则点$E$一定落在$CO$的延长线上，$\angle DCE$即直线$CD$与平面$ABC$所成的角。不妨设$AB = 2$，在$Rt\triangle EOD$中，$DO=\sqrt{3}$，$\angle EOD = 180^{\circ}-150^{\circ}=30^{\circ}$，则$DE=\frac{\sqrt{3}}{2}$，$EO=\frac{3}{2}$。又$CO=\frac{1}{2}AB = 1$，所以$EC=\frac{5}{2}$，$\tan\angle DCE=\frac{DE}{EC}=\frac{\sqrt{3}}{5}$，故选C。

21. [全国甲理 2022·7,5 分]在长方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中,已知$B_{1}D$与平面$ABCD$和平面$AA_{1}B_{1}B$所成的角均为$30^{\circ}$,则(D)

A.$AB = 2AD$
B.$AB$与平面$AB_{1}C_{1}D$所成的角为$30^{\circ}$
C.$AC = CB_{1}$
D.$B_{1}D$与平面$BB_{1}C_{1}C$所成的角为$45^{\circ}$

答案：
21.D [解析]在长方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，设$AB = a$，$BC = b$，$CC_{1}=c$。连接$BD$，因为$BB_{1}\perp$平面$ABCD$，所以$B_{1}D$与平面$ABCD$所成的角为$\angle BDB_{1}$，即$\angle BDB_{1}=30^{\circ}$，所以$\tan\angle BDB_{1}=\frac{\sqrt{3}}{3}=\frac{c}{\sqrt{a^{2}+b^{2}}}$ ①。
因为$DA\perp$平面$A_{1}ABB_{1}$，所以$B_{1}D$与平面$A_{1}ABB_{1}$所成的角为$\angle AB_{1}D$，即$\angle AB_{1}D = 30^{\circ}$，所以$\tan\angle AB_{1}D=\frac{\sqrt{3}}{3}=\frac{b}{\sqrt{a^{2}+c^{2}}}$ ②。
由①②可得$a=\sqrt{2}b=\sqrt{2}c$，故A不正确。
过点$B$作线段$AB_{1}$的垂线，垂足为$O$，连接$DO$，由A可知$BB_{1}=c$，$AB=\sqrt{2}c$，$AB_{1}=\sqrt{3}c$，则$BO=\frac{\sqrt{6}}{3}c$，$B_{1}O=\frac{\sqrt{3}}{3}c$，又$AD = c$，则$DO=\frac{\sqrt{21}}{3}c$，所以$DO^{2}+BO^{2}=BD^{2}$，所以$BO\perp DO$。
又因为$DO\cap AB_{1}=O$，$DO,AB_{1}\subset$平面$AB_{1}D$，所以$BO\perp$平面$AB_{1}D$，所以$AB$与平面$AB_{1}D$所成的角为$\angle OAB$。在$Rt\triangle AOB$中，$\sin\angle OAB=\frac{BO}{AB}=\frac{\frac{\sqrt{6}}{3}c}{\sqrt{2}c}=\frac{\sqrt{3}}{3}$，故B不正确。
因为$AC=\sqrt{a^{2}+b^{2}}=\sqrt{3}c$，$CB_{1}=\sqrt{b^{2}+c^{2}}=\sqrt{2}c$，故C不正确。易知$B_{1}D$与平面$BB_{1}C_{1}C$所成的角为$\angle DB_{1}C$，而$DC = BC=\sqrt{2}c$，且$DC\perp B_{1}C$，所以$\angle DB_{1}C = 45^{\circ}$，故D正确。故选D。

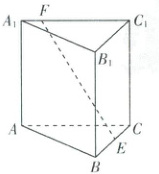
22. [浙江 2022·8,4 分]如图,已知正三棱柱$ABC - A_{1}B_{1}C_{1}$,$AC = AA_{1}$,$E$,$F$分别是棱$BC$,$A_{1}C_{1}$上的点.记$EF$与$AA_{1}$所成的角为$\alpha$,$EF$与平面$ABC$所成的角为$\beta$,二面角$F - BC - A$的平面角为$\gamma$,则(A)


A.$\alpha \leq \beta \leq \gamma$
B.$\beta \leq \alpha \leq \gamma$
C.$\beta \leq \gamma \leq \alpha$
D.$\alpha \leq \gamma \leq \beta$

答案：
22.A [解析]如图，过点$F$作$FH\perp AC$于点$H$，连接$EH$。由题知，正三棱柱的各棱长都相等，易知$FH// AA_{1}$，则$\angle EFH$即为$EF$与$AA_{1}$所成的角，则$\angle EFH=\alpha$，$\angle FEH=\beta$，且$FH\geqslant EH$，所以$\alpha\leqslant\beta$。在$AB$上取$AM = AF$，过点$M$作$MN\perp AB$于点$N$，连接$NH,CF,BM$，则$NH// MF// B_{1}C_{1}// BC$，所以$NH$与$BC$之间的距离$d\leqslant EH$。又$\tan\gamma=\frac{FH}{d}=\frac{AA_{1}}{d}$，$\tan\beta=\frac{FH}{EH}=\frac{AA_{1}}{EH}$，所以$\tan\gamma\geqslant\tan\beta$，所以$\beta\leqslant\gamma$，所以$\alpha\leqslant\beta\leqslant\gamma$，故选A。

23. [全国一 2025·17,15 分]如图,在四棱锥$P - ABCD$中,$PA \perp$底面$ABCD$,$AB \perp AD$,$BC // AD$.
(1)证明:平面$PAB \perp$平面$PAD$;
(2)设$PA = AB = \sqrt{2}$,$BC = 2$,$AD = 1 + \sqrt{3}$,且点$P$,$B$,$C$,$D$均在球$O$的球面上.
(ⅰ)证明:点$O$在平面$ABCD$内;
(ⅱ)求直线$AC$与$PO$所成角的余弦值.
]

答案：
23.
(1) [证明]由题意知，在四棱锥$P - ABCD$中，$PA\perp$平面$ABCD$，$AB\perp AD$，$AB\subset$平面$ABCD$，$AD\subset$平面$ABCD$，$\therefore AP\perp AB$，$AP\perp AD$。
$\because AP\subset$平面$PAD$，$AD\subset$平面$PAD$，$AP\cap AD = A$，$\therefore AB\perp$平面$PAD$。
$\because AB\subset$平面$PAB$，$\therefore$平面$PAB\perp$平面$PAD$。
(2)(i) [证明] $\because P,B,C,D$在同一个球面上，$\therefore$球心到四个点的距离相等。
在$\triangle BCD$中，到三角形三个顶点距离相等的点是该三角形的外心，作出$BC$的垂直平分线，交$AD$于$O$，连接$BO$，$CO$，如图所示，
由图可知$OE = AB=\sqrt{2}$，$BE = CE = AO=\frac{1}{2}BC = 1$，$O_{1}D=AD - AO=\sqrt{3}$，
$BO = CO=\sqrt{1^{2}+(\sqrt{2})^{2}}=\sqrt{3}$，
$\therefore O_{1}D = BO = CO$，
$\therefore$点$O$是$\triangle BCD$的外心。
在$Rt\triangle AOP$中，$AP\perp AD$，$AP=\sqrt{2}$，由勾股定理得，$PO=\sqrt{AP^{2}+AO^{2}}=\sqrt{(\sqrt{2})^{2}+1^{2}}=\sqrt{3}$，
$\therefore PO = BO = CO = O_{1}D=\sqrt{3}$，
$\therefore$点$O$即为点$P,B,C,D$所在球的球心$O$，
此时点$O$在线段$AD$上，$AD\subset$平面$ABCD$，
$\therefore$点$O$在平面$ABCD$内。
(ii) [解]由(i)可知，$PO=\sqrt{3}$，
$\because AB\perp AD$，$BC// AD$，$\therefore AB\perp BC$，
在$Rt\triangle ABC$中，$AB=\sqrt{2}$，$BC = 2$，由勾股定理得$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{(\sqrt{2})^{2}+2^{2}}=\sqrt{6}$，
过点$O$作$AC$的平行线，交$BC$的延长线于$C_{1}$，连接$AC_{1}$，$PC_{1}$，如图所示，
$\because AD// BC$，$\therefore$四边形$AOC_{1}C$为平行四边形，$OC_{1}=AC=\sqrt{6}$，直线$AC$与直线$PO$所成角为$\angle POC_{1}$或其补角。
$\because PA\perp$平面$ABCD$，$AC\subset$平面$ABCD$，$\therefore PA\perp AC$，
在$Rt\triangle ABC_{1}$中，$AB=\sqrt{2}$，$BC_{1}=BC + CC_{1}=2 + 1 = 3$，由勾股定理得$AC_{1}=\sqrt{AB^{2}+BC_{1}^{2}}=\sqrt{(\sqrt{2})^{2}+3^{2}}=\sqrt{11}$，
在$Rt\triangle APC_{1}$中，$PA=\sqrt{2}$，由勾股定理得$PC_{1}=\sqrt{PA^{2}+AC_{1}^{2}}=\sqrt{(\sqrt{2})^{2}+(\sqrt{11})^{2}}=\sqrt{13}$，
在$\triangle POC_{1}$中，由余弦定理得$PC_{1}^{2}=PO^{2}+OC_{1}^{2}-2PO· OC_{1}·\cos\angle POC_{1}$，
即$(\sqrt{13})^{2}=(\sqrt{3})^{2}+(\sqrt{6})^{2}-2×\sqrt{3}×\sqrt{6}×\cos\angle POC_{1}$，
解得$\cos\angle POC_{1}=-\frac{\sqrt{2}}{3}$，
$\therefore$直线$AC$与直线$PO$所成角的余弦值为$\cos(\pi-\angle POC_{1})=\frac{\sqrt{2}}{3}$。

24. [全国新高考Ⅱ2021·19,12 分]如图,在四棱锥$Q - ABCD$中,底面$ABCD$为正方形,$AD = 2$,$QC = 3$,$QA = QD = \sqrt{5}$.
(1)证明:平面$QAD \perp$平面$ABCD$;
(2)求二面角$B - QD - A$的余弦值.
]

答案：
24.
(1) [证明]如图，取$AD$中点$E$，连接$EQ,EC$。
因为$QA = QD=\sqrt{5}$，所以$QE\perp AD$。
在正方形$ABCD$中，$AD = 2$，则$QE = 2$，且$EC=\sqrt{5}$，此时$EQ^{2}+EC^{2}=9 = QC^{2}$，
则$QE\perp EC$。
又$EC\cap AD = E$，$EC,AD\subset$平面$ABCD$，所以$QE\perp$平面$ABCD$。
因为$QE\subset$平面$QAD$，所以平面$QAD\perp$平面$ABCD$。
(2) [解]过点$A$作$AF\perp QD$交$QD$于点$F$，连接$BF$。在等腰三角形$AQD$中，利用等面积法可得$AF=\frac{QE· AD}{QD}=\frac{2×2}{\sqrt{5}}=\frac{4\sqrt{5}}{5}$，则$QF=\sqrt{QA^{2}-AF^{2}}=\sqrt{5-\frac{16}{5}}=\frac{3\sqrt{5}}{5}$。结合
(1)易得$AB\perp$平面$QAD$，则$AB\perp AQ$，$AB\perp AF$，因此$BQ = 3$。在$\triangle BQD$中利用余弦定理可得$\cos\angle BQD=\frac{BQ^{2}+QD^{2}-BD^{2}}{2BQ· QD}=\frac{9 + 5-8}{2×3×\sqrt{5}}=\frac{\sqrt{5}}{5}$，又$\frac{QF}{BQ}=\frac{\sqrt{5}}{5}$，所以$\cos\angle BQD=\frac{QF}{BQ}$，则$\angle QFB=\frac{\pi}{2}$，即$BF\perp QD$。因此$\angle AFB$为二面角$B - QD - A$的平面角。
$BF=\sqrt{BQ^{2}-QF^{2}}=\frac{6\sqrt{5}}{5}$，在$Rt\triangle AFB$中，$\cos\angle AFB=\frac{AF}{BF}=\frac{2}{3}$，因此二面角$B - QD - A$的余弦值为$\frac{2}{3}$。