《2026年高中必刷题高中数学必修第二册人教版》

二问题3−组数据的众数一定存在，且是唯一的吗？

答案： 提示 一般来说，一组数据中,出现次数最多的数称为这组数据的众数，例如:1,2,3,3,4的众数是3.如果有两个或两个以上的数出现次数都是最多的,那么这几个数都是这组数据的众数,例如:1,2,2,3,3,4的众数是2和3.如果所有数据出现的次数都一样,那么这组数据没有众数,例如:1,2,3,4,5没有众数.

二问题4众数、中位数、平均数应用时有何区分？

答案： 提示 一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数,而对分类型数据(如校服规格、性别、产品质量等级等)
集中趋势的描述，可以用众数.
二问题5数据的离散程度可以通过什么来衡量？标准差的大小对数据的
离散程度有何影响？
提示 数据的离散程度可以通过极差、方差或标准差来衡量.其中极差是一组数据中最大值与最小值的差，它反映了一组数据变化的最大幅度，它对一组数据中的极端值非常敏感.方差则反映了一组数据围绕平均数波动的大小.为了得到以样本数据的单位表示的波动幅度,通常使用标准差一样本方差的算术平方根.标准差越大,表明数据的离散程度就越大;反之,标准差越小,表明数据的离散程度就越超过极差.小.它用来描述样本数据的离散程度.在实际应用中,标准差常被理解为稳定性.

[例1] 某地区为了了解知识分子的年龄结构,随机抽取50名知识分子,其年龄分别如下:
42,38,29,36,41,43,54,43,34,44,
40,59,39,42,44,50,37,44,45,29,
48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,67,
53,49,65,47,54,63,57,43,46,58.
印象笔记
二(1)众数一定在原始数
据中.
(2)众数只是出现次数最
多的数，但无法确定多的
程度
因为方差与原始数据的
单位不同，且平方后可能
夸大了偏差的程度，所以
虽然方差与标准差在刻画
样本数据的离散程度上是
一样的，但在解决实际问
题中，一般多采用标准差.
二(1)标准差的大小不会
(2)标准差、方差的取值
范围为[0,+∞).标准差、
方差为0时，样本中各数
据全相等，表明数据没有
波动幅度，数据没有离
散性.
组距和组数的确定没
有固定的标准，将数据分
组时，组数力求合适，使
数据的分布规律能较清
楚地呈现出来，组数太多
或太少，都会影响我们了

答案：
解数据的分布情况.当样
本量不超过100时，常分
成5~12组，一般样本量
越大，所分组数也越多.
狂K重点
(1)列出样本的频率分布表;
(2)画出样本的频率分布直方图;
(3)估计年龄在[32,52)中的知识分子所占的比例.
解:
(1)极差为67−2______8=39,取组距为5,分为8组,样本频率分布表如下:
分组 频数累计 频数 频率
[232) F 3 0.06
[3$\frac{7,}{2}$,$\frac{3}{4}$42) 正TF 28 0.04
$\frac{[37}{[42}$,47)正正正− 16 $\frac{0.16}{0.32}$
[[4572,,5527]) $\frac{正F}{正}$ 58 00..1160
[57,62) 正 4
62,67] 正 4 $\frac{0.08}{0.08}$
合计 50 $\frac{0.08}{1.00}$
(2)样本的频率分布直方图如图所示.

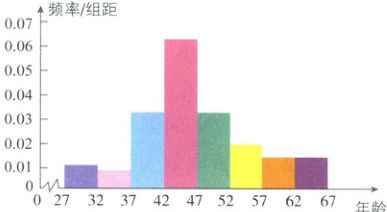
(3)由样本的频率分布表估计年龄在[32,52)中的知识分子所占的比例约为0.04+0.16+0.32+0.16=0.68=68%.
拓展2其他形式的统计图表
高中阶段常见的统计图表,除了频率分布表和频率分布直方图之外,还有条形分布表从数量上比较准图、扇形图、折线图.
条形图
用宽度相同的长方形的高度或长短来表示数据的多少.条形图可以横置或纵置,纵置时也称为柱形图.条形图有简单条形图、复合条形图等形式.
①条形图的主要特点
(1)能够直观地看出各个数据的大小;
(2)易于比较数据之间的差别.
②条形图与频率分布直方图的区别
(1)条形图往往是用长方形的高度表示频数的大小,而频率分布直方图实际上是用长方形的面积表示频率;
(2)条形图中,横轴上的数据是孤立的,是一个具体的数据,而频率分布直方图中,横轴上的数据是连续的,是一个范围;
(3)条形图中,各长方形之间有空隙,而频率分布直方图中，各长方形是靠在一起的