《2026年高中必刷题高中数学必修第二册人教版》

1. [河南漯河高中 2025 高一期中]已知 $\alpha,\beta,\gamma$ 为不同的平面，$m,n,l$ 为不同的直线，则下列条件中一定能得到 $m\perp\beta$ 的是(C)

A.$\alpha\cap\gamma = m,\alpha\perp\gamma,\beta\perp\gamma$
B.$\alpha\perp\beta,\alpha\cap\beta = l,m\perp l$
C.$n\perp\alpha,n\perp\beta,m\perp\alpha$
D.$\alpha\perp\gamma,\beta\perp\gamma,m\perp\alpha$

答案： 1.C【解析】在选项A中，$\alpha \cap \gamma=m$，$\alpha \bot \gamma$，$\beta \bot \gamma$，则$\beta$和$m$可能平行或相交，故A错误；在选项B中，$\alpha \bot \beta$，$\alpha \cap \beta=l$，$m \bot l$，则$m$与$\beta$相交或$m // \beta$或$m \subset \beta$，故B错误；在选项C中，因为$n \bot \alpha$，$n \bot \beta$，所以$\alpha // \beta$，又$m \bot \alpha$，所以$m \bot \beta$，故C正确；在选项D中，由$\alpha \bot \gamma$，$\beta \bot \gamma$，不能推出$\alpha // \beta$，
㊙点睛〗“墙角”模型中三个平面两两垂直所以由$m \bot \alpha$不能推出$m \bot \beta$，故D错误.故选C.

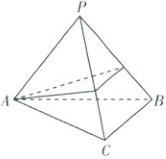
2. [广东东莞 2024 高一月考]如图，在三棱锥 $P - ABC$ 中，$AB = AC = 2,S_{\triangle ABC} = 1,\angle BAC$ 为锐角，侧棱 $PA = PB = PC = 2$，一只小虫从 $A$ 点出发，沿侧面绕棱锥爬行一周后回到 $A$ 点，则小虫爬行的最短距离为(D)

A.$2\sqrt{2}$
B.$2\sqrt{3}$
C.$\sqrt{6}-\sqrt{2}$
D.$\sqrt{6}+\sqrt{2}$

答案：
2.D【解析】在三棱锥$P - ABC$中，$AB = AC = 2$，$S_{\triangle ABC} = 1$，则有$S_{\triangle ABC} = \frac{1}{2}AB· AC· \sin\angle BAC = 1$，可得$\sin\angle BAC = \frac{1}{2}$，又$\angle BAC$为锐角，所以$\angle BAC = 30^{\circ}$.因为$PB = PC = 2$，所以$\triangle ABC \cong \triangle PBC$，所以$\angle BPC = \angle BAC = 30^{\circ}$，将三棱锥侧面沿侧棱$PA$展开，连接$AA'$，则$\angle APA' = 60^{\circ} + 60^{\circ} + 30^{\circ} = 150^{\circ}$，如图，根据余弦定理得所求最短距离$d = \sqrt{2^2 + 2^2 - 2×2×2×\cos150^{\circ}} = \sqrt{6} + \sqrt{2}$，故选D.

3. [安徽芜湖一中 2025 高一期中]已知直四棱柱的高为 2，其底面四边形 $ABCD$ 水平放置时的斜二测直观图为矩形 $A'B'C'D'$，如图所示. 若 $A'O' = O'B' = B'C' = 1$，则该直四棱柱的表面积为(C)


A.$20 + 4\sqrt{2}$
B.$8 + 2(\sqrt{2}+\sqrt{3})$
C.$20 + 8\sqrt{2}$
D.$8 + 4(\sqrt{2}+\sqrt{3})$

答案：
3.C【解析】由直观图可得底面四边形$ABCD$水平放置时的平面图形如图所示，由$A'O' = O'B' = B'C' = 1$，得$AO = OB = 1$，$C'O' = \sqrt{O'B'^2 + B'C'^2} = \sqrt{2}$，所以$OC = 2\sqrt{2}$.
㊙黑板〗由直观图推断平面图形内各边的实际长度时，优先从位于坐标轴上的边开始考虑则$S_{四边形ABCD} = 2×2\sqrt{2} = 4\sqrt{2}$，$BC = \sqrt{OC^2 + OB^2} = 3$，所以此直棱柱的底面周长$C_{四边形ABCD} = 2×(2 + 3) = 10$.又直棱柱的高$h = 2$，所以该直棱柱的侧面积$S_{侧面积} = C_{四边形ABCD}· h = 20$，则表面积$S_{表面积} = S_{侧面积} + 2S_{四边形ABCD} = 20 + 8\sqrt{2}$.故选C.

4. [江苏镇江 2025 高一质量检测]已知一圆台上底面半径为 1(下底面半径大于上底面半径)，母线与底面所成角的余弦值为 $\frac{1}{3}$，若此圆台存在内切球(球与圆台各面均相切)，则此圆台的表面积是(C)

A.$5\pi$
B.$9\pi$
C.$14\pi$
D.$23\pi$

答案：
4.C【解析】设圆台的上底面半径为$r_1 = 1$，下底面半径为$r_2$，如图，作出圆台的轴截面，过点$C$作$CM\bot AB$，垂足为$M$，
设内切球$O$与梯形两腰分别切于点$E,F$，可知$BC = r_1 + r_2$，$BM = r_2 - r_1$，
㊙点悟〗内切球体现在轴截面上即为内切圆由题意可知，$\frac{BM}{BC} = \frac{r_2 - r_1}{r_1 + r_2} = \frac{1}{3}$，可得$r_2 = 2$，即$BC = 3$，则此圆台的表面积是$S_{圆台} = \pi×1^2 + \pi×2^2 + \pi(1 + 2)×3 = 14\pi$.故选C.

5. 在正方体 $ABCD - A_1B_1C_1D_1$ 中，$E$ 是 $BB_1$ 的中点. 若 $AB = 6$，则点 $B$ 到平面 $ACE$ 的距离为(B)

A.$\sqrt{5}$
B.$\sqrt{6}$
C.$\frac{3\sqrt{6}}{2}$
D.$3$

答案： 5.B【解析】在正方体$ABCD - A_1B_1C_1D_1$中，$AB = 6$，$E$是$BB_1$的中点，则$BE = 3$，$AE = CE = \sqrt{6^2 + 3^2} = 3\sqrt{5}$，$AC = 6\sqrt{2}$，$\therefore S_{\triangle ACE} = \frac{1}{2}×6\sqrt{2}×\sqrt{(3\sqrt{5})^2 - (3\sqrt{2})^2} = 9\sqrt{6}$.设点$B$到平面$ACE$的距离为$h$，由$V_{E - ABC} = V_{B - ACE}$，得$\frac{1}{3}×\frac{1}{2}×6×6×3 = \frac{1}{3}×9\sqrt{6}h$，解得$h = \sqrt{6}$.故选B.

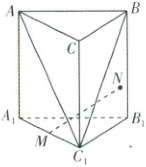
6. [陕西西北工业大学附属中学 2025 高一期中]如图，在三棱柱 $ABC - A_1B_1C_1$ 中，$M$ 为 $A_1C_1$ 的中点，$N$ 为侧面 $BCC_1B_1$ 上的一点，且 $MN//$ 平面 $ABC_1$. 若点 $N$ 的轨迹长度为 2，则(B)

A.$AC_1 = 4$
B.$BC_1 = 4$
C.$AB_1 = 6$
D.$B_1C = 6$

答案：
6.B【解析】如图，取$B_1C_1$的中点$D$，$BB_1$的中点$E$，连接$MD$，$DE$，$ME$，
则$MD// A_1B_1// AB$，$DE// BC_1$，又$MD\not\subset$平面$ABC_1$，$ABC_1\subset$平面$ABC_1$，所以$MD//$平面$ABC_1$，同理可得$DE//$平面$ABC_1$，又$MD\cap DE = D$，$MD,DE\subset$平面$MDE$，所以平面$MDE//$平面$ABC_1$，又$MN//$平面$ABC_1$，所以点$N$的轨迹为线段$DE$，由$DE = \frac{1}{2}BC_1 = 2$，可得$BC_1 = 4$.故选B.

7. [浙江绍兴诸暨中学 2025 高一期中]已知四棱锥 $S - ABCD$ 的所有顶点都在球 $O$ 的球面上，$SD\perp$ 平面 $ABCD$，底面 $ABCD$ 是等腰梯形，$AB// CD$ 且满足 $AB = 2AD = 2DC = 2,\angle ADC = 120^{\circ},SC = \sqrt{5}$，则球 $O$ 的体积是(B)

A.$\frac{8}{3}\pi$
B.$\frac{8\sqrt{2}}{3}\pi$
C.$8\sqrt{2}\pi$
D.$8\pi$

答案：
7.B【解析】如图，连接$BD$，因为$AB// CD$，$\angle ADC = 120^{\circ}$，所以$\angle BAD = 60^{\circ}$，在$\triangle ABD$中，由余弦定理可得$BD = \sqrt{AD^2 + AB^2 - 2AD· AB·\cos\angle BAD} = \sqrt{3}$，又$AB = 2AD = 2$，所以$AD^2 + BD^2 = AB^2$，所以$AD\bot BD$，所以$\triangle ABD$的外心是$AB$的中点$N$，连接$NC$，因为$2CD = AB$，$AB// CD$，所以$CD = AN$，$CD// AN$，所以四边形$ADCN$是平行四边形，所以$NC = AD = 1$，从而$N$是梯形$ABCD$的外接圆的圆心，连接$ND$，此时$ND = 1$.过$N$作$ON\bot$平面$ABCD$，$O$为四棱锥$S - ABCD$的外接球的球心，
因为$SD\bot$平面$ABCD$，$DCC\subset$平面$ABCD$，所以$SD\bot DC$，又因为$SC = \sqrt{5}$，所以$SD = \sqrt{SC^2 - 1} = 2$，所以$ON = 1$，所以$OB = \sqrt{1 + 1} = \sqrt{2}$，所以球$O$的体积$V = \frac{4}{3}\pi· OB^3 = \frac{8\sqrt{2}}{3}\pi$.故选B.

8. [山东省实验中学 2025 高一月考]已知三棱锥 $P - ABC$，$Q$ 为 $BC$ 的中点，$PB = PC = AB = BC = AC = 2$，侧面 $PBC\perp$ 底面 $ABC$，则过点 $Q$ 的平面截该三棱锥外接球所得截面面积的取值范围为(A)

A.$\left[\pi,\frac{5\pi}{3}\right]$
B.$\left[\frac{\pi}{2},\frac{2\pi}{3}\right]$
C.$\left[\frac{2\pi}{3},2\pi\right]$
D.$[\pi,2\pi]$

答案：
8.A【解析】如图，连接$PQ$，$QA$，由$PB = PC = AB = BC = AC = 2$可知，$\triangle ABC$和$\triangle PBC$均是等边三角形，设三棱锥$P - ABC$外接球的球心为$O$，则球心$O$到平面$ABC$和平面$PBC$的射影是$\triangle ABC$和$\triangle PBC$的中心$E,F$，因为$Q$为$BC$的中点，所以$PQ\bot BC$，又因为侧面$PBC\bot$底面$ABC$，侧面$PBC\cap$底面$ABC = BC$，$PQ\subset$侧面$PBC$，所以$PQ\bot$底面$ABC$，而$AQC\subset$底面$ABC$，因此$PQ\bot AQ$，所以四边形$OFQE$是矩形，又$\triangle ABC$和$\triangle PBC$均是边长为$2$的等边三角形，所以两个三角形的高$h = \sqrt{2^2 - (\frac{1}{2}×2)^2} = \sqrt{3}$，在矩形$OFQE$中，$OE = FQ = \frac{1}{3}h = \frac{\sqrt{3}}{3}$，$AE = \frac{2}{3}h = \frac{2\sqrt{3}}{3}$，$OF = EQ = \frac{1}{3}h = \frac{\sqrt{3}}{3}$，连接$OA$，所以$OA = \sqrt{OE^2 + EA^2} = \sqrt{\frac{1}{3}^2 + \frac{4}{3}^2} = \frac{\sqrt{15}}{3}$，连接$OQ$，设过点$Q$的平面为$\alpha$，当$OQ\bot\alpha$时，此时所得截面的面积最小，该截面为圆形，$OQ = \sqrt{OF^2 + FQ^2} = \sqrt{(\frac{1}{3})^2 + (\frac{1}{3})^2} = \frac{\sqrt{2}}{3}×\sqrt{3} = \frac{\sqrt{6}}{3}$，因此圆$Q$的半径为$\sqrt{OA^2 - OQ^2} = \sqrt{\frac{15}{9} - \frac{6}{9}} = 1$，所以此时截面面积为$\pi·1^2 = \pi$；当点$Q$在以$O$为圆心的大圆上时，截面的面积最大，最大面积为$\pi×(\frac{\sqrt{15}}{3})^2 = \frac{5\pi}{3}$，所以所求截面面积的取值范围为$[\pi,\frac{5\pi}{3}]$.故选A.