《2026年高中必刷题高中数学必修第二册人教版》

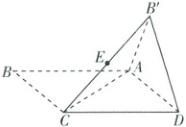
7. [河北廊坊2025高一月考]已知菱形$ABCD$的边长为2，$\angle ABC=60^{\circ}$。将菱形沿对角线$AC$折叠成大小为$60^{\circ}$二面角$B'-AC-D$。设$E$为$B'C$的中点，$F$为三棱锥$B'-ACD$表面上一动点，且总满足$AC\perp EF$，则点$F$轨迹的长度为$\frac{3\sqrt{3}}{2}$。

答案：
7.$\frac{3\sqrt{3}}{2}$【解析】如图，取$AC$的中点$T$，连接$B^{\prime}T$，$DT$，因为菱形$ABCD$的边长为$2$，$\angle ABC = 60^{\circ}$，
所以$B^{\prime}C = AB^{\prime} = CD = AD = AC$，$\triangle ACD$，$\triangle ACB^{\prime}$均为等边三角形，所以$DT\perp AC$，$B^{\prime}T\perp AC$，且$DT = B^{\prime}T = \sqrt{3}$，$\angle B^{\prime}TD$为二面角$B^{\prime}-AC - D$的平面角，则$\angle B^{\prime}TD = 60^{\circ}$，
故$\triangle B^{\prime}TD$为等边三角形，则$DB^{\prime} = \sqrt{3}$.
又$B^{\prime}T\cap DT = T$，$B^{\prime}T$，$DT\subset$平面$B^{\prime}TD$，
所以$AC\perp$平面$B^{\prime}TD$.
取$CT$的中点$O$，$CD$的中点$N$，
连接$EO$，$EN$，$ON$，又$E$为$B^{\prime}C$的中点，则$EO// B^{\prime}T$，$ON// TD$，$EN// B^{\prime}D$，且$EO = ON = EN = \frac{\sqrt{3}}{2}$，
因为$EO\subset$平面$EON$，$B^{\prime}T\not\subset$平面$EON$，所以$B^{\prime}T//$平面$EON$，
同理得$B^{\prime}D//$平面$EON$，
因为$B^{\prime}T\cap B^{\prime}D = B^{\prime}$，$B^{\prime}T$，$B^{\prime}D\subset$平面$B^{\prime}TD$，
所以平面$EON//$平面$B^{\prime}TD$，
所以$AC\perp$平面$EON$，
故点$F$的轨迹为$\triangle EON$(除点$E$外)，
➠避坑：当点$F$与点$E$重合时，直线$EF$不存在，不符合题意
故点$F$轨迹的长度为$EO + ON + EN = \frac{3\sqrt{3}}{2}$.

8. 已知点$S,A,B,C$均在半径为4的球$O$的表面上，且$SA\perp$平面$ABC,SA=4,\angle BAC=\frac{2\pi}{3},AB=2\sqrt{3}$，点$M$在$BC$上，当直线$SM$与平面$ABC$所成的角最大时，$AM=$$\sqrt{3}$。

答案：
8.$\sqrt{3}$【解析】设$\triangle ABC$的外接圆的圆心为$H$，半径为$R$，$SA$的中点为$E$，外接球的球心为$O$，连接$OE$，$OH$，$OA$，$AH$，则$OH\perp$平面$ABC$，$OE\perp SA$，
因为$SA\perp$平面$ABC$，所以$OH// SA$，所以$E$，$O$，$H$四点共面，
因为$AH\subset$平面$ABC$，所以$SA\perp AH$，所以$AH// EO$，故四边形$AEOH$为矩形.
因为$R = \frac{1}{2}×\frac{BC}{\sin\angle BAC} = \frac{BC}{\sqrt{3}}$，所以在$Rt\triangle AOE$中，$(\frac{BC}{\sqrt{3}})^2 + (\frac{1}{2}×4)^2 = 16$，解得$BC = 6$.
在$\triangle ABC$中，由余弦定理得$BC^{2} = AB^{2}+AC^{2}-2AB· AC·(-\frac{1}{2})$，即$36 = 12 + AC^{2}+2\sqrt{3}AC$，解得$AC = 2\sqrt{3}$，故$AC = AB$，故$\angle CBA = \angle ACB = \frac{\pi}{6}$，
因为$SA\perp$平面$ABC$，所以$\angle SMA$为直线$SM$与平面$ABC$所成的角，
当$AM$长度最小时，$\angle SMA$最大，此时$AM\perp BC$，故$AM = 2\sqrt{3}×\frac{1}{2} = \sqrt{3}$.

9. [浙江宁波2025高一期末]如图，六面体$ABCDEF$中，四边形$ABCD$为菱形，$AE=2BF,BF// AE,BF\perp AD$，且平面$ACE\perp$平面$ABCD$。
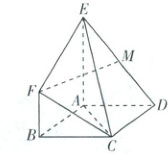
(1)点$M$是棱$DE$的中点，求证：$FM//$平面$ABCD$；
(2)求证：$AE\perp$平面$ABCD$；
(3)若$AB=AC=BF=2$，求二面角$A-CE-D$的余弦值。

答案：
9.
(1)【证明】如图，取$AD$的中点$N$，连接$MN$，$BN$，
由$M$，$N$分别为$DE$，$AD$的中点，得$MN// AE$，且$AE = 2MN$，
由$BF// AE$，且$AE = 2BF$，得$BF// MN$，$BF = MN$，
则四边形$BFMN$为平行四边形，
则$FM// BN$.
因为$FM\not\subset$平面$ABCD$，$BN\subset$平面$ABCD$，
所以$FM//$平面$ABCD$.

(2)【证明】连接$BD$，由四边形$ABCD$为菱形，得$AC\perp BD$，
由平面$ACE\perp$平面$ABCD$，且平面$ACE\cap$平面$ABCD = AC$，$BD\subset$平面$ABCD$，
得$BD\perp$平面$ACE$.
由$AE\subset$平面$ACE$，得$BD\perp AE$.
由$BF\perp AD$，$BF// AE$，得$AE\perp AD$，
由$AD\cap BD = D$，$AD$，$BD\subset$平面$ABCD$，得$AE\perp$平面$ABCD$.
(3)【解】设$O$为$AC$与$BD$的交点，由
(2)
可知$DO\perp$平面$ACE$，$EC\subset$平面$ACE$，
所以$DO\perp EC$，作$OH\perp CE$，垂足为$H$，连接$DH$，
因为$DO\cap OH = O$，$DO$，$OH\subset$平面$DOH$，所以$EC\perp$平面$DOH$.因为$DH\subset$平面$DOH$，所以$EC\perp DH$，所以$\angle DHO$为二面角$A - CE - D$的平面角.
因为$AB = AC = 2$，四边形$ABCD$为菱形，所以$DO = \sqrt{3}$，$OC = 1$，
又$BF = 2$，$AE = 2BF$，所以$AE = 4$，$EC = \sqrt{AE^{2}+AC^{2}} = \sqrt{4^{2}+2^{2}} = 2\sqrt{5}$，
由$\triangle COH\sim\triangle CEA$，得$\frac{OH}{EA} = \frac{OC}{EC}$，即$\frac{OH}{4} = \frac{1}{2\sqrt{5}}$，所以$OH = \frac{2\sqrt{5}}{5}$.
因为$OH\subset$平面$ACE$，所以$OH\perp DO$.
在$Rt\triangle OHD$中，$\tan\angle OHD = \frac{OD}{OH} = \frac{\sqrt{15}}{2}$，所以$\cos\angle OHD = \frac{2}{\sqrt{19}} = \frac{2\sqrt{19}}{19}$，故二面角$A - CE - D$的余弦值为$\frac{2\sqrt{19}}{19}$.

10. [吉林省吉林市2025高一期中]如图，在正四棱锥$P-ABCD$中，所有棱长均为$a$，点$R$是棱$PC$的中点，点$Q$是底面$ABCD$内任意一点，点$Q$到侧面$PAB,PBC,PCD,PDA$的距离分别为$d_1,d_2,d_3,d_4$。
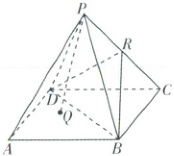
(1)证明：平面$PBC\perp$平面$BRD$；
(2)求直线$BR$与底面$ABCD$所成角的正切值；
(3)求$d_1+d_2+d_3+d_4$。

答案：
10.
(1)【证明】因为在正四棱锥$P - ABCD$中，所有棱长均为$a$，点$R$是棱$PC$的中点，所以$PC\perp DR$，$PC\perp BR$，
又$DR\cap BR = R$，$DR$，$BR\subset$平面$BRD$，所以$PC\perp$平面$BRD$，
又$PC\subset$平面$PBC$，所以平面$PBC\perp$平面$BRD$.
(2)【解】如图，设$AC\cap BD = O$，点$E$为$OC$的中点，连接$PO$，$BE$，$RE$，
在正四棱锥$P - ABCD$中，$PO\perp$平面$ABCD$.
在$\triangle POC$中，点$E$为$OC$的中点，点$R$为$PC$的中点，
所以$RE// PO$，且$RE = \frac{1}{2}PO$，
所以$RE\perp$平面$ABCD$.
因为$BE\subset$平面$ABCD$，
所以$BE\perp RE$，所以$\angle RBE$即为直线$BR$与底面$ABCD$所成的角.
因为正四棱锥$P - ABCD$的所有棱长均为$a$，
所以$AC = \sqrt{AB^{2}+BC^{2}} = \sqrt{2}a$，$PO = \sqrt{PA^{2}-(\frac{AC}{2})^{2}} = \frac{\sqrt{2}}{2}a$，
所以$RE = \frac{1}{2}PO = \frac{\sqrt{2}}{4}a$；$EC = \frac{1}{4}AC = \frac{\sqrt{2}}{4}a$，
在$\triangle BCE$中，由余弦定理可得$BE = \sqrt{BC^{2}+EC^{2}-2BC· EC·\cos\frac{\pi}{4}} = \frac{\sqrt{10}}{4}a$，
所以$\tan\angle RBE = \frac{RE}{BE} = \frac{\sqrt{5}}{5}$.

(3)【解】设点$P$到平面$ABCD$的距离为$h = PO = \frac{\sqrt{2}}{2}a$，因为正四棱锥$P - ABCD$的所有棱长均为$a$，
所以四个侧面的正三角形的面积均为$\frac{1}{2}a^{2}\sin60^{\circ} = \frac{\sqrt{3}}{4}a^{2}$，底面正方形的面积为$a^{2}$，
依题意可得$V_{P - ABCD} = V_{Q - PAB}+V_{Q - PBC}+V_{Q - PCD}+V_{Q - PDA}$，
所以$\frac{1}{3}a^{2}h = \frac{1}{3}S_{\triangle PAB}d_{1}+\frac{1}{3}S_{\triangle PBC}d_{2}+\frac{1}{3}S_{\triangle PCD}d_{3}+\frac{1}{3}S_{\triangle PDA}d_{4}$，
即$a^{2}×\frac{\sqrt{2}}{2}a = \frac{\sqrt{3}}{4}a^{2}(d_{1}+d_{2}+d_{3}+d_{4})$，解得$d_{1}+d_{2}+d_{3}+d_{4} = \frac{2\sqrt{6}}{3}a$.

11. [福建部分学校2024高一联考]《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑。在如图所示的阳马$P-ABCD$中，侧棱$PD\perp$底面$ABCD$，且$PD=CD=2$，点$E$是$PC$的中点，连接$DE,BD,BE$。
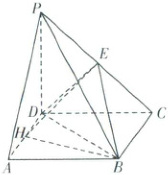
(1)证明：$DE\perp$平面$PBC$。试判断四面体$EBCD$是否为鳖臑。若是，写出其每个面的直角（只需写出结论）；若不是，请说明理由。
(2)设点$H$是$AD$的中点，若二面角$E-BD-C$的大小为$\frac{\pi}{3}$，求三棱锥$E-HBD$的外接球的表面积。

答案：
11.【解】
(1)因为$PD\perp$底面$ABCD$，$BC\subset$底面$ABCD$，所以$PD\perp BC$.
因为底面$ABCD$为长方形，
所以$BC\perp CD$.
因为$PD\cap CD = D$，$PD$，$CD\subset$平面$PCD$，
所以$BC\perp$平面$PCD$.
因为$DE\subset$平面$PCD$，$PC\subset$平面$PCD$，
所以$BC\perp DE$，$BC\perp PC$.
因为$PD = CD$，点$E$是$PC$的中点，
所以$DE\perp PC$.
因为$PC\cap BC = C$，$PC$，$BC\subset$平面$PBC$，
所以$DE\perp$平面$PBC$.
因为$EB\subset$平面$PBC$，所以$DE\perp EB$，所以四面体$EBCD$的四个面都是直角三角形，即四面体$EBCD$是一个鳖臑，其四个面的直角分别是$\angle BCD$，$\angle BCE$，$\angle DEC$，$\angle DEB$.
(2)如图①，取$DC$的中点$F$，连接$EF$，过点$F$作$FG\perp BD$于点$G$，连接$EG$.

因为$E$，$F$分别是$PC$，$DC$的中点，所以$EF// PD$，
又$PD\perp$底面$ABCD$，所以$EF\perp$平面$ABCD$.因为$BD$，$FG\subset$平面$ABCD$，所以$EF\perp BD$，$EF\perp FG$.
又因为$FG\perp BD$，$EF\cap FG = F$，$EF$，$FG\subset$平面$EFG$，
所以$BD\perp$平面$EFG$.因为$EG\subset$平面$EFG$，所以$BD\perp EG$，所以$\angle EGF$就是二面角$E - BD - C$的平面角，所以$\angle EGF = \frac{\pi}{3}$.
设$AD = t$，
由$\angle FGD = \angle BCD = \frac{\pi}{2}$，可知$\triangle DFG\sim\triangle DBC$，所以$\frac{DF}{BD} = \frac{FG}{BC}$，所以$FG = \frac{t}{\sqrt{t^{2}+4}}$，所以$\tan\angle EGF = \frac{EF}{FG} = \sqrt{3}$，又$EF = \frac{1}{2}PD = 1$，所以$FG = \frac{\sqrt{3}}{3}$，
所以$\frac{t}{\sqrt{t^{2}+4}} = \frac{\sqrt{3}}{3}$，解得$t = \sqrt{2}$.
因为$CD = 2$，$AD = \sqrt{2}$，所以$BD = \sqrt{6}$，$DH = \frac{\sqrt{2}}{2}$，所以$HB = \sqrt{AH^{2}+AB^{2}} = \frac{3\sqrt{2}}{2}$，
所以$\cos\angle DHB = \frac{DH^{2}+HB^{2}-BD^{2}}{2· DH· HB} = -\frac{1}{3}$，所以$\sin\angle DHB = \frac{2\sqrt{2}}{3}$.
如图②，设$\triangle DHB$的外接圆半径为$r$，外接圆圆心为$O$，连接$OB$，$OD$，$OH$，
则$2r = \frac{BD}{\sin\angle DHB} = \frac{3\sqrt{3}}{2}$，则$r = DO = HO = \frac{3\sqrt{3}}{4}$，
在底面$ABCD$中，过点$O$作$OM\perp CD$，$OK\perp DH$，垂足分别为$M$，$K$，连接$OF$，

则$OM = DK = \frac{1}{2}DH = \frac{\sqrt{2}}{4}$，则$DM = \sqrt{DO^{2}-OM^{2}} = \frac{5}{4}$，
又$DF = 1$，所以$FM = \frac{1}{4}$，所以$FO = \sqrt{(\frac{\sqrt{3}}{4})^{2}+(\frac{1}{4})^{2}}=\frac{\sqrt{3}}{4}$
设三棱锥$E - HBD$的外接球球心为$O_1$，球的半径为$R$，连接$OO_1$，并设$OO_1 = \lambda(\lambda＞0)$，
若球心$O_1$和点$E$位于平面$DHB$的异侧，如图③，连接$O_1H$，$O_1E$，
➠避坑：注意球心$O_1$的位置，构造的三角形不同，可能会影响结果
则$R = HO_1 = \sqrt{(\frac{3\sqrt{3}}{4})^{2}+\lambda^{2}} = EO_1 = \sqrt{(\frac{\sqrt{3}}{4})^{2}+(1 + \lambda)^{2}}$，解得$\lambda = \frac{1}{4}$，
则$R = \frac{\sqrt{7}}{2}$
若球心$O_1$和点$E$位于平面$DHB$同侧，则$R = HO_1 = \sqrt{(\frac{3\sqrt{3}}{4})^{2}+\lambda^{2}} = EO_1 = \sqrt{(\frac{\sqrt{3}}{4})^{2}+(1 - \lambda)^{2}}$，解得$\lambda = -\frac{1}{4}$(舍去).
综上，三棱锥$E - HBD$的外接球的表面积$S = 4\pi R^{2} = 7\pi$.