2026年高中必刷题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年高中必刷题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [上海华东政法大学附属中学2025高二阶段性检测]下列关于二面角的平面角的说法,正确的是(
A.两条边分别在二面角的两个面内的角
B.过二面角棱上一点且两边分别垂直于棱的角
C.二面角的两个面被一个垂直于棱的平面所截得的角
D.任一个平面去截二面角的两个面所得的角
C
)A.两条边分别在二面角的两个面内的角
B.过二面角棱上一点且两边分别垂直于棱的角
C.二面角的两个面被一个垂直于棱的平面所截得的角
D.任一个平面去截二面角的两个面所得的角
答案:
1.C [解析]过二面角棱上一点在两个半平面内作棱的垂线,两条射线所成的角叫做二面角的平面角.
对于A,两条边不一定垂直于棱,故A错误;对于B,两边不一定在平面内,故B错误;对于C,二面角的两个面被一个垂直于棱的平面所截得的角,此时棱垂直于平面与二面角的两个半平面的两条交线,并且两条交线分别在两个半平面内,符合二面角的平面角定义,故C正确;
对于D,由C知,棱不一定垂直于平面与二面角的两个半平面的两条交线,故D错误
故选C.
对于A,两条边不一定垂直于棱,故A错误;对于B,两边不一定在平面内,故B错误;对于C,二面角的两个面被一个垂直于棱的平面所截得的角,此时棱垂直于平面与二面角的两个半平面的两条交线,并且两条交线分别在两个半平面内,符合二面角的平面角定义,故C正确;
对于D,由C知,棱不一定垂直于平面与二面角的两个半平面的两条交线,故D错误
故选C.
2. 在二面角的棱$l$上任选一点$O$,若$\angle AOB$是二面角$\alpha - l - \beta$的平面角,则必须具有条件(
A.$AO \perp BO$,$AO \subset \alpha$,$BO \subset \beta$
B.$AO \perp l$,$BO \perp l$
C.$AB \perp l$,$AO \subset \alpha$,$BO \subset \beta$
D.$AO \perp l$,$BO \perp l$,且$AO \subset \alpha$,$BO \subset \beta$
D
)A.$AO \perp BO$,$AO \subset \alpha$,$BO \subset \beta$
B.$AO \perp l$,$BO \perp l$
C.$AB \perp l$,$AO \subset \alpha$,$BO \subset \beta$
D.$AO \perp l$,$BO \perp l$,且$AO \subset \alpha$,$BO \subset \beta$
答案:
2.D [解析]根据题意,l是平面α与β的交线,则根据二面角的定义,若AO⊥l,
BO⊥l,且AO⊂α,BO⊂β,则∠AOB为二面角α−l−β的平面角.故选D.
BO⊥l,且AO⊂α,BO⊂β,则∠AOB为二面角α−l−β的平面角.故选D.
3. [河南郑州2025高一联考]如图,点$B$在以$AC$为直径的圆$O$的圆周上,$\angle AOB = \frac{\pi}{3}$,$PA \perp$平面$ABC$,$2PA = AC = 4$,则二面角$P - BC - A$的平面角为(

A.$\frac{\pi}{2}$
B.$\frac{\pi}{3}$
C.$\frac{\pi}{4}$
D.$\frac{\pi}{6}$
C
)
A.$\frac{\pi}{2}$
B.$\frac{\pi}{3}$
C.$\frac{\pi}{4}$
D.$\frac{\pi}{6}$
答案:
3.C [解析]
∵∠AOB=$\frac{\pi}{3}$,OA=OB=2,
∴△AOB为等边三角形,
∴AB=2.
∵点B在以AC为直径的圆O的圆周上,
∴AB⊥BC;
∵PA⊥平面ABC,BC⊂平面
ABC,AB⊂平面ABC,
∴PA⊥BC,PA⊥AB.又
∵PA∩AB=A,PA,AB⊂平面PAB,
∴BC⊥平面PAB.
∵PB⊂平面PAB,
∴BC⊥PB,
∴∠PBA是二面角P−BC−A的平面角.
又
∵AB=PA=2,PA⊥AB,
∴∠PBA=$\frac{\pi}{4}$.故选C.
∵∠AOB=$\frac{\pi}{3}$,OA=OB=2,
∴△AOB为等边三角形,
∴AB=2.
∵点B在以AC为直径的圆O的圆周上,
∴AB⊥BC;
∵PA⊥平面ABC,BC⊂平面
ABC,AB⊂平面ABC,
∴PA⊥BC,PA⊥AB.又
∵PA∩AB=A,PA,AB⊂平面PAB,
∴BC⊥平面PAB.
∵PB⊂平面PAB,
∴BC⊥PB,
∴∠PBA是二面角P−BC−A的平面角.
又
∵AB=PA=2,PA⊥AB,
∴∠PBA=$\frac{\pi}{4}$.故选C.
4. 已知在三棱锥$S - ABC$中,$SA \perp SB$,$SB \perp SC$,$SA \perp SC$,且$\triangle ABC$为等边三角形,则二面角$S - AB - C$的正切值为(
A.$\frac{\sqrt{3}}{2}$
B.$\sqrt{2}$
C.$\sqrt{3}$
D.$2$
B
)A.$\frac{\sqrt{3}}{2}$
B.$\sqrt{2}$
C.$\sqrt{3}$
D.$2$
答案:
4.B [解析]由SA⊥SB,SB⊥SC,SA⊥SC以及AB=BC=AC可得△SAC≌△SBC,△SAC≌△SAB,故SC=SA=SB,则AB=$\sqrt{2}$SA,不妨设SA=2,则AB=2√2,
如图,取AB的中点M,连接MS,MC,故MS⊥AB,MC⊥AB,故∠SMC即为二面角S−AB−C的平面角.

因为SB⊥SC,SA⊥SC,SA∩SB=S,SA,SB⊂平面SAB,所以SC⊥平面SAB.因为SM⊂平面SAB,所以SC⊥SM,所以tan∠SMC=$\frac{SC}{SM}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,故选B.
4.B [解析]由SA⊥SB,SB⊥SC,SA⊥SC以及AB=BC=AC可得△SAC≌△SBC,△SAC≌△SAB,故SC=SA=SB,则AB=$\sqrt{2}$SA,不妨设SA=2,则AB=2√2,
如图,取AB的中点M,连接MS,MC,故MS⊥AB,MC⊥AB,故∠SMC即为二面角S−AB−C的平面角.

因为SB⊥SC,SA⊥SC,SA∩SB=S,SA,SB⊂平面SAB,所以SC⊥平面SAB.因为SM⊂平面SAB,所以SC⊥SM,所以tan∠SMC=$\frac{SC}{SM}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,故选B.
5. [河北邯郸2025高一期中]已知一个正四棱锥的侧棱与底面所成角的正切值为$2$,则该四棱锥侧面与底面所成二面角的正弦值为(
A.$\frac{\sqrt{2}}{3}$
B.$\frac{2\sqrt{5}}{5}$
C.$\frac{1}{3}$
D.$\frac{2\sqrt{2}}{3}$
D
)A.$\frac{\sqrt{2}}{3}$
B.$\frac{2\sqrt{5}}{5}$
C.$\frac{1}{3}$
D.$\frac{2\sqrt{2}}{3}$
答案:
5.D [解析]如图,在正四棱锥P−ABCD中,记O是底面的中心,E是BC的中点,连接PO,AC,BD,PE,OE,可知PO⊥平面ABCD,则∠PBO是侧棱PB与底面所成的角,由题意可得tan∠PBO=2,则
sin∠PBO=$\frac{2\sqrt{5}}{5}$,cos∠PBO=$\frac{\sqrt{5}}{5}$.
由正四棱锥的结构特征可知PE⊥BC,OE⊥BC,则∠PEO是该四棱锥侧面与底面所成二面角的平面角

设正四棱锥的底面边长为a,则OB=
$\frac{1}{2}$BD=$\frac{1}{2}$$\sqrt{a²+a²}$=$\frac{\sqrt{2}}{2}$a,所以PB=
$\sqrt{5}$OB=$\frac{\sqrt{10}}{2}$a,PO=2OB=$\sqrt{2}$a,
点悟:通过∠PBO的余弦值、正切值求得PB,PO
所以PE=$\sqrt{PB²−BE²}$=
$\sqrt{(\frac{\sqrt{10}}{2}a)^2-(\frac{1}{2}a)^2}$=$\frac{3}{2}$a,
所以sin∠PEO=$\frac{PO}{PE}$=$\frac{\sqrt{2}a}{\frac{3}{2}a}$=$\frac{2\sqrt{2}}{3}$,即该四
棱锥侧面与底面所成二面角的正弦值为$\frac{2\sqrt{2}}{3}$.故选D.
5.D [解析]如图,在正四棱锥P−ABCD中,记O是底面的中心,E是BC的中点,连接PO,AC,BD,PE,OE,可知PO⊥平面ABCD,则∠PBO是侧棱PB与底面所成的角,由题意可得tan∠PBO=2,则
sin∠PBO=$\frac{2\sqrt{5}}{5}$,cos∠PBO=$\frac{\sqrt{5}}{5}$.
由正四棱锥的结构特征可知PE⊥BC,OE⊥BC,则∠PEO是该四棱锥侧面与底面所成二面角的平面角

设正四棱锥的底面边长为a,则OB=
$\frac{1}{2}$BD=$\frac{1}{2}$$\sqrt{a²+a²}$=$\frac{\sqrt{2}}{2}$a,所以PB=
$\sqrt{5}$OB=$\frac{\sqrt{10}}{2}$a,PO=2OB=$\sqrt{2}$a,
点悟:通过∠PBO的余弦值、正切值求得PB,PO
所以PE=$\sqrt{PB²−BE²}$=
$\sqrt{(\frac{\sqrt{10}}{2}a)^2-(\frac{1}{2}a)^2}$=$\frac{3}{2}$a,
所以sin∠PEO=$\frac{PO}{PE}$=$\frac{\sqrt{2}a}{\frac{3}{2}a}$=$\frac{2\sqrt{2}}{3}$,即该四
棱锥侧面与底面所成二面角的正弦值为$\frac{2\sqrt{2}}{3}$.故选D.
6. [山东烟台2025高一月考]在矩形$ABCD$中,$AB = 3$,$AD = 4$,$PA \perp$平面$ABCD$,$PA = \sqrt{3}$,则二面角$P - BD - A$的正切值为
$\frac{5\sqrt{3}}{12}$
。
答案:
6.$\frac{5\sqrt{3}}{12}$[解析]如图,过点A作AE⊥BD于点E,连接PE,因为PA⊥平面ABCD,
AE,BD⊂平面ABCD,所以PA⊥AE,PA⊥BD.
又因为AE∩PA=A,AE,PA⊂平面PAE,所以BD⊥平面PAE.
又PE⊂平面PAE,所以BD⊥PE,
所以∠PEA即为二面角P−BD−A的平面角.由题知BD=$\sqrt{3²+4²}$=5,
由S△ABD=$\frac{1}{2}$AD·AB=$\frac{1}{2}$AE·BD,
得AE=$\frac{AD·AB}{BD}$=$\frac{12}{5}$,
所以tan∠PEA=$\frac{PA}{AE}$=$\frac{\sqrt{3}}{\frac{12}{5}}$=$\frac{5\sqrt{3}}{12}$,
即二面角P−BD−A的正切值为$\frac{5\sqrt{3}}{12}$.

6.$\frac{5\sqrt{3}}{12}$[解析]如图,过点A作AE⊥BD于点E,连接PE,因为PA⊥平面ABCD,
AE,BD⊂平面ABCD,所以PA⊥AE,PA⊥BD.
又因为AE∩PA=A,AE,PA⊂平面PAE,所以BD⊥平面PAE.
又PE⊂平面PAE,所以BD⊥PE,
所以∠PEA即为二面角P−BD−A的平面角.由题知BD=$\sqrt{3²+4²}$=5,
由S△ABD=$\frac{1}{2}$AD·AB=$\frac{1}{2}$AE·BD,
得AE=$\frac{AD·AB}{BD}$=$\frac{12}{5}$,
所以tan∠PEA=$\frac{PA}{AE}$=$\frac{\sqrt{3}}{\frac{12}{5}}$=$\frac{5\sqrt{3}}{12}$,
即二面角P−BD−A的正切值为$\frac{5\sqrt{3}}{12}$.

7. [浙江宁波慈溪2025高一期末]已知直线$a$,$b$与平面$\alpha$,$\beta$,则能使$\alpha \perp \beta$的充分条件是(
A.$a \perp \alpha$,$b \perp \beta$,$a // b$
B.$a \subset \alpha$,$b \subset \beta$,$a \perp b$
C.$a // b$,$a \perp \beta$,$b \subset \alpha$
D.$\alpha \cap \beta = a$,$b \perp a$,$b \subset \beta$
C
)A.$a \perp \alpha$,$b \perp \beta$,$a // b$
B.$a \subset \alpha$,$b \subset \beta$,$a \perp b$
C.$a // b$,$a \perp \beta$,$b \subset \alpha$
D.$\alpha \cap \beta = a$,$b \perp a$,$b \subset \beta$
答案:
7.C [解析]对于A,由a⊥α,a//b,得b⊥α,而b⊥β,则α//β,A不符合题意;
对于B,若α//β,a,b分别是平面α,β内互相垂直的异面直线,满足a⊂α,b⊂β,a⊥b,B不符合题意;
对于C,由a//b,a⊥β,得b⊥β,又b⊂α,则α⊥β,C符合题意;
对于D,由α∩β=a,b⊥a,b⊂β,得二面角α−a−β的平面角可以是锐角、直角,也可以是钝角,D不符合题意故选C.
对于B,若α//β,a,b分别是平面α,β内互相垂直的异面直线,满足a⊂α,b⊂β,a⊥b,B不符合题意;
对于C,由a//b,a⊥β,得b⊥β,又b⊂α,则α⊥β,C符合题意;
对于D,由α∩β=a,b⊥a,b⊂β,得二面角α−a−β的平面角可以是锐角、直角,也可以是钝角,D不符合题意故选C.
8. 如图,$PA$垂直于正方形$ABCD$所在平面,连接$PB$,$PC$,$PD$,$AC$,$BD$,则下列垂直关系正确的是(

①平面$PAB \perp$平面$PAD$;
②平面$PAB \perp$平面$PBC$;
③平面$PAB \perp$平面$PCD$;
④平面$PAB \perp$平面$PAC$。
A.①②
B.①③
C.②③
D.②④
A
)
①平面$PAB \perp$平面$PAD$;
②平面$PAB \perp$平面$PBC$;
③平面$PAB \perp$平面$PCD$;
④平面$PAB \perp$平面$PAC$。
A.①②
B.①③
C.②③
D.②④
答案:
8.A [解析]
∵PA⊥平面ABCD,BC⊂平面
ABCD,
∴PA⊥BC.又正方形ABCD中,
BC⊥AB,PA∩AB=A,PA,AB⊂平面PAB,
∴BC⊥平面PAB,又BC⊂平面PBC,
∴平面PAB⊥平面PBC,②正确
同理AD⊥平面PAB,AD⊂平面PAD,
∴平面PAD⊥平面PAB,①正确
设平面PAB∩平面PCD=l,
∵AB//CD,
AB⊂平面PAB,CD⊄平面PAB,
∴CD//平面PAB,
∴CD//l.又易得CD⊥平面PAD,
∴l⊥平面PAD,P为垂足,
∴∠APD为二面角A−l−D的平面角,若平面PAB⊥平面PCD,则AP⊥PD,在Rt△PAD中不可能存在AP⊥PD,③错误
∵AB⊥PA,AC⊥PA,
∴∠BAC为二面角
B−PA−C的平面角,若平面PAB⊥平面PAC,则AB⊥AC,在Rt△ABC中不可能存在AB⊥AC,④错误故选A.
∵PA⊥平面ABCD,BC⊂平面
ABCD,
∴PA⊥BC.又正方形ABCD中,
BC⊥AB,PA∩AB=A,PA,AB⊂平面PAB,
∴BC⊥平面PAB,又BC⊂平面PBC,
∴平面PAB⊥平面PBC,②正确
同理AD⊥平面PAB,AD⊂平面PAD,
∴平面PAD⊥平面PAB,①正确
设平面PAB∩平面PCD=l,
∵AB//CD,
AB⊂平面PAB,CD⊄平面PAB,
∴CD//平面PAB,
∴CD//l.又易得CD⊥平面PAD,
∴l⊥平面PAD,P为垂足,
∴∠APD为二面角A−l−D的平面角,若平面PAB⊥平面PCD,则AP⊥PD,在Rt△PAD中不可能存在AP⊥PD,③错误
∵AB⊥PA,AC⊥PA,
∴∠BAC为二面角
B−PA−C的平面角,若平面PAB⊥平面PAC,则AB⊥AC,在Rt△ABC中不可能存在AB⊥AC,④错误故选A.
9. (多选)[天津河东区2024高一期末]如图,$PA$垂直于以$AB$为直径的圆所在的平面,$C$为圆上异于$A$,$B$的任意一点,$AE \perp PC$,垂足为$E$,点$F$是$PB$上一点,则下列判断中正确的是(
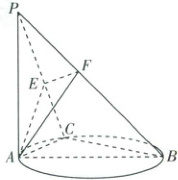
A.$BC \perp$平面$PAC$
B.$AE \perp EF$
C.$AC \perp PB$
D.平面$AEF \perp$平面$PBC$
ABD
)
A.$BC \perp$平面$PAC$
B.$AE \perp EF$
C.$AC \perp PB$
D.平面$AEF \perp$平面$PBC$
答案:
9.ABD [解析]对于A,PA垂直于以AB为直径的圆所在的平面,而BC⊂平面
ABC,则PA⊥BC,又由圆的性质可知AC⊥
BC,且PA∩AC=A,PA,AC⊂平面PAC,则
BC⊥平面PAC,所以A正确
对于B,由A可知BC⊥AE,又AE⊥PC,且
BC∩PC=C,BC,PC⊂平面PCB,所以
AE⊥平面PCB,而EF⊂平面PCB,所以
AE⊥EF,所以B正确
对于C,已知AC⊥BC,若AC⊥PB,则由
BC∩PB=B,BC,PB⊂平面PCB,可知
AC⊥平面PCB,所以AC⊥PC,即∠PCA=
90°,在Rt△PAC中,∠PAC=90°,矛盾,则
AC⊥PB不成立,所以C错误
对于D,由B可知,AE⊥平面PBC,
又AE⊂平面AEF,故平面AEF⊥平面PBC,所以D正确,故选ABD.
ABC,则PA⊥BC,又由圆的性质可知AC⊥
BC,且PA∩AC=A,PA,AC⊂平面PAC,则
BC⊥平面PAC,所以A正确
对于B,由A可知BC⊥AE,又AE⊥PC,且
BC∩PC=C,BC,PC⊂平面PCB,所以
AE⊥平面PCB,而EF⊂平面PCB,所以
AE⊥EF,所以B正确
对于C,已知AC⊥BC,若AC⊥PB,则由
BC∩PB=B,BC,PB⊂平面PCB,可知
AC⊥平面PCB,所以AC⊥PC,即∠PCA=
90°,在Rt△PAC中,∠PAC=90°,矛盾,则
AC⊥PB不成立,所以C错误
对于D,由B可知,AE⊥平面PBC,
又AE⊂平面AEF,故平面AEF⊥平面PBC,所以D正确,故选ABD.
10. [广东深圳2025高一期中]如图,在四棱锥$P - ABCD$中,底面$ABCD$是直角梯形,$AD // BC$,$AB \perp BC$,$AB = BC = 1$,$AD = 2$,$PA \perp$平面$ABCD$,$PA = 2$。
(1)求证:$CD \perp$平面$PAC$;
(2)求证:平面$PAC \perp$平面$PCD$;
(3)求二面角$P - CD - A$的余弦值。
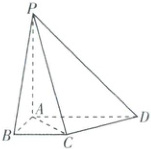
(1)求证:$CD \perp$平面$PAC$;
(2)求证:平面$PAC \perp$平面$PCD$;
(3)求二面角$P - CD - A$的余弦值。

答案:
10.
(1)[证明]由AB⊥BC,AB=BC=1,得
AC=$\sqrt{AB²+BC²}$=$\sqrt{2}$

如图,取AD的中点F,连接CF,
因为∠BAD=90°,AB=BC=AF=1,AF//
BC,所以四边形ABCF是正方形.
则CF=1,CF⊥AF,则CD=$\sqrt{FD²+FC²}$=
$\sqrt{2}$.又因为AD=2,
所以AC²+CD²=2+2=4=AD²,
所以AC⊥CD.
又因为PA⊥平面ABCD,CD⊂平面
ABCD,所以PA⊥CD.
又因为PA∩AC=A,且PA,AC⊂平面PAC,
所以CD⊥平面PAC.
(2)[证明]由
(1)知CD⊥平面PAC,
CD⊂平面PCD,所以平面PAC⊥平面PCD.
(3)[解]因为CD⊥平面PAC,PC⊂平面PAC,所以PC⊥CD,又因为AC⊥CD,所以∠PCA为二面角P−CD−A的平面角.
因为PA⊥平面ABCD,AC⊂平面
ABCD,所以PA⊥AC.
在Rt△PAC中,AC=$\sqrt{2}$,PA=2,
则PC=$\sqrt{AC²+PA²}$=$\sqrt{6}$,则cos∠PCA=
$\frac{AC}{PC}$=$\frac{\sqrt{2}}{\sqrt{6}}$=$\frac{\sqrt{3}}{3}$.
归纳总结证明平面与平面垂直的方法
(1)利用定义:证明二面角的平面角为直角,其判定的步骤是:①找出两相交半平面的平面角;②证明这个平面角是直角;③得出这两个相交半平面互相垂直
(2)利用面面垂直的判定定理:要证面面垂直,只要证线面垂直,即在其中一个平面内寻找一条直线与另一个平面垂直,这是证明面面垂直的常用方法,其基本步骤:
定思路 分析题意,根据题目条件选择证明哪个平面的垂线
证线面 选择恰当方法证明线面垂直
定面面 根据面面垂直的判定定理证明

10.
(1)[证明]由AB⊥BC,AB=BC=1,得
AC=$\sqrt{AB²+BC²}$=$\sqrt{2}$

如图,取AD的中点F,连接CF,
因为∠BAD=90°,AB=BC=AF=1,AF//
BC,所以四边形ABCF是正方形.
则CF=1,CF⊥AF,则CD=$\sqrt{FD²+FC²}$=
$\sqrt{2}$.又因为AD=2,
所以AC²+CD²=2+2=4=AD²,
所以AC⊥CD.
又因为PA⊥平面ABCD,CD⊂平面
ABCD,所以PA⊥CD.
又因为PA∩AC=A,且PA,AC⊂平面PAC,
所以CD⊥平面PAC.
(2)[证明]由
(1)知CD⊥平面PAC,
CD⊂平面PCD,所以平面PAC⊥平面PCD.
(3)[解]因为CD⊥平面PAC,PC⊂平面PAC,所以PC⊥CD,又因为AC⊥CD,所以∠PCA为二面角P−CD−A的平面角.
因为PA⊥平面ABCD,AC⊂平面
ABCD,所以PA⊥AC.
在Rt△PAC中,AC=$\sqrt{2}$,PA=2,
则PC=$\sqrt{AC²+PA²}$=$\sqrt{6}$,则cos∠PCA=
$\frac{AC}{PC}$=$\frac{\sqrt{2}}{\sqrt{6}}$=$\frac{\sqrt{3}}{3}$.
归纳总结证明平面与平面垂直的方法
(1)利用定义:证明二面角的平面角为直角,其判定的步骤是:①找出两相交半平面的平面角;②证明这个平面角是直角;③得出这两个相交半平面互相垂直
(2)利用面面垂直的判定定理:要证面面垂直,只要证线面垂直,即在其中一个平面内寻找一条直线与另一个平面垂直,这是证明面面垂直的常用方法,其基本步骤:
定思路 分析题意,根据题目条件选择证明哪个平面的垂线
证线面 选择恰当方法证明线面垂直
定面面 根据面面垂直的判定定理证明

查看更多完整答案,请扫码查看


