《2026年高中必刷题高中数学必修第二册人教版》

16. [河北邢台2025高一期中联考] 在直四棱柱 $ ABCD - A_{1}B_{1}C_{1}D_{1} $ 中，四边形 $ ABCD $ 是菱形，$ \angle ABC = 60^{\circ} $，$ 2AA_{1} = 3AB $，$ E $ 是棱 $ A_{1}D_{1} $ 的中点，则直线 $ BE $ 与平面 $ ABCD $ 所成角的余弦值是(A)

A.$ \dfrac{\sqrt{7}}{4} $
B.$ \dfrac{3}{4} $
C.$ \dfrac{1}{2} $
D.$ \dfrac{\sqrt{3}}{2} $

答案：
16.A【解析】如图，取棱AD的中点F，连接$B_1F$，$BF$，$EF$，又E是棱$A_1D_1$的中点，所以$EF// AA_1$.
因为$AA_1\perp$平面ABCD，所以$EF\perp$平面ABCD，则$\angle EBF$是直线BE与平面ABCD所成的角.
设$AB = 2$，则$EF = AA_1 = 3$，$AF = 1$，又$\angle BAF = 120^{\circ}$，在$\triangle ABF$中，由余弦定理可得$BF = \sqrt{AB^2 + AF^2 - 2AB· AF\cos\angle BAF}=\sqrt{7}$，则$BE = \sqrt{BF^2 + EF^2}=4$，所以$\cos\angle EBF=\frac{BF}{BE}=\frac{\sqrt{7}}{4}$.故选A.
归纳总结 求直线与平面所成角的步骤：作（或找）出斜线在平面上的射影，将空间角转化为平面角；过斜线上斜足以外的一点作平面的垂线，再过垂足和斜足作直线即为射影.注意斜线上点的选取以及垂足的位置要与问题中已知量有关，才能便于计算；证明某平面角就是斜线与平面所成的角；通常在垂线段、斜线段和射影所组成的直角三角形中计算.

17. [江西宜春2025高一期中] 已知正四棱台的上底边长为 $ 2 $，下底边长为 $ 4 $，侧棱与底面所成的角为 $ 60^{\circ} $，则此四棱台的体积为(A)

A.$ \dfrac{28\sqrt{6}}{3} $
B.$ 28\sqrt{6} $
C.$ \dfrac{28\sqrt{3}}{3} $
D.$ 28\sqrt{3} $

答案：
17.A【解析】如图，不妨记正四棱台为$ABCD - A_1B_1C_1D_1$，S,O分别为上底面和下底面的中心，连接$OS$，$A_1S$，$AO$.
由正四棱台的性质可知$OS\perp$底面ABCD，过点$A_1$作$A_1T\perp AO$于点T，易知$A_1$，$A$，$S$，$O$四点共面，因为$SO\perp$底面ABCD，$AO\subset$底面ABCD，所以$SO\perp AO$，所以$A_1T// SO$，所以$A_1T\perp$底面ABCD，所以$\angle A_1AT$是侧棱与底面所成的角.
因为上、下底面边长分别为2和4，所以$A_1S = \sqrt{2}$，$AO = 2\sqrt{2}$，
所以$TO = A_1S = \sqrt{2}$，所以$AT = AO - OT=\sqrt{2}$，所以$\tan\angle A_1AT=\frac{A_1T}{AT}$.因为侧棱与底面所成的角为$60^{\circ}$，所以$\angle A_1AT = 60^{\circ}$，故$A_1T = \sqrt{3}AT=\sqrt{6}$.
则该正四棱台的体积为$\frac{1}{3}×(2^2 + 4^2 + \sqrt{2^2×4^2})×\sqrt{6}=\frac{28\sqrt{6}}{3}$.故选A.

18. [陕西商洛2024高一期末] 在正三棱柱 $ ABC - A_{1}B_{1}C_{1} $ 中，$ AA_{1} = AB $，$ M $ 是 $ AB $ 的中点，$ N $ 是棱 $ B_{1}C_{1} $ 上的动点，则直线 $ MN $ 与平面 $ BCC_{1}B_{1} $ 所成角的正切值的最大值为(D)

A.$ \dfrac{1}{2} $
B.$ \dfrac{\sqrt{2}}{2} $
C.$ \dfrac{\sqrt{3}}{2} $
D.$ \dfrac{\sqrt{3}}{4} $

答案：
18.D【解析】如图，过点M作$MG\perp BC$，垂足为G，连接NG.在正三棱柱$ABC - A_1B_1C_1$中，$CC_1\perp$平面ABC，因为$MG\subset$平面ABC，所以$CC_1\perp MG$.
因为$BC\cap CC_1 = C$，$BC$،$CC_1\subset$平面$BCC_1B_1$，
所以$MG\perp$平面$BCC_1B_1$，故$\angle MNG$为直线MN与平面$BCC_1B_1$所成的角.
当$\angle MNG$取得最大值时，$\tan\angle MNG=\frac{MG}{NG}$取得最大值，且MG为定值，则NG取得最小值.
点悟：将角的最值问题转化成线段长的最值问题是关键
不妨设$AA_1 = AB = a$，则$MG = MB\sin\angle ABC=\frac{1}{2}a·\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}a$，NG的最小值为a，
此时$\tan\angle MNG=\frac{MG}{NG}=\frac{\sqrt{3}}{4}$.故选D.

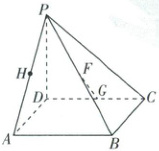
19. [湖北武汉五校2025高一期末] 如图，在四棱锥 $ P - ABCD $ 中，底面 $ ABCD $ 是边长为 $ 2 $ 的菱形，$ \angle DAB = 60^{\circ} $，$ \triangle PAD $ 是以 $ PA $ 为斜边的等腰直角三角形，$ \triangle PCD $ 是以 $ PC $ 为斜边的等腰直角三角形，$ F $，$ G $，$ H $ 分别是 $ PB $，$ CD $，$ PA $ 的中点.
(1) 求证：$ GF // $ 平面 $ PAD $；
(2) 求直线 $ PB $ 与平面 $ ABCD $ 所成角的大小.

答案：
19.
(1)【证明】连接FH,HD.
因为F为PB的中点，H为PA的中点，所以$HF// AB$，且$HF=\frac{1}{2}AB$，
又因为四边形ABCD为菱形，且G为CD的中点，
所以$DG// AB$，且$DG=\frac{1}{2}AB$，
所以$HF// DG$，且$HF = DG$，所以四边形HDGF为平行四边形，
所以$GF// HD$.
因为$GF\not\subset$平面PAD，$HD\subset$平面PAD，所以$GF//$平面PAD.

(2)【解】连接BD，由题知$PD\perp AD$，$PD\perp CD$，且$AD$，$CD\subset$平面ABCD，$AD\cap CD = D$，所以$PD\perp$平面ABCD，又$BD\subset$平面ABCD，所以直线PB与平面ABCD所成角即为$\angle PBD$.
在菱形ABCD中，$\angle DAB = 60^{\circ}$，所以$BD = AB = AD = 2$，
在$\triangle PAD$中，$PD = AD = 2$，
所以在$Rt\triangle PBD$中，$PD = BD = 2$，所以该三角形为等腰直角三角形.
所以$\angle PBD = 45^{\circ}$，即直线PB与平面ABCD所成角为$45^{\circ}$.

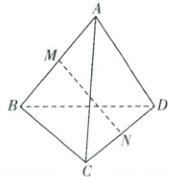
20. [浙江杭州外国语学校2024高一期中]如图，在四面体$A - BCD$中，$AC = 2$，$BD = \sqrt{2}$，$AC$与$BD$所成的角为$45^{\circ}$，$M$，$N$分别为$AB$，$CD$的中点，则线段$MN$的长为$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{10}}{2}$。

答案：
20.$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{10}}{2}$ [解析]如图，取BC的中点E，连接EM,EN，
　　　　　
∵M,E分别为AB,BC的中点，
∴ME//AC且ME=$\frac{1}{2}$AC=1，
同理可得EN//BD且EN=$\frac{1}{2}$BD=$\frac{\sqrt{2}}{2}$，
∴∠MEN(或其补角)为异面直线AC与BD所成的角，则∠MEN=45°或135°。
避坑：注意这里∠MEN为异面直线AC与BD所成角的补角的情况，否则容易漏解
在△MEN中，EM=1,EN=$\frac{\sqrt{2}}{2}$，
若∠MEN=45°，则由余弦定理可得MN=$\sqrt{EM^{2}+EN^{2}-2EM· EN\cos45^{\circ}}$
=$\sqrt{1^{2}+(\frac{\sqrt{2}}{2})^{2}-2×1×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}}=\frac{\sqrt{2}}{2}$；
若∠MEN=135°，则由余弦定理可得MN=$\sqrt{EM^{2}+EN^{2}-2EM· EN\cos135^{\circ}}$
=$\sqrt{1^{2}+(\frac{\sqrt{2}}{2})^{2}-2×1×(-\frac{\sqrt{2}}{2})×\frac{\sqrt{2}}{2}}=\frac{\sqrt{10}}{2}$
综上所述，MN=$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{10}}{2}$。
易错警示：异面直线所成角的范围是$(0,\frac{\pi}{2}]$。利用平移作异面直线所成角时，作出的角不一定是异面直线所成角，还可能是异面直线所成角的补角，需要进行分类讨论。

21. 如图，正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的棱长为$1$，过点$A$作平面$A_{1}BD$的垂线，垂足为$H$，有下面三个结论：

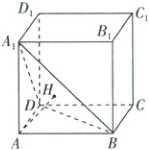
①$H$是$\triangle A_{1}BD$的中心；
②$AH \perp$平面$CB_{1}D_{1}$；
③直线$AC_{1}$与直线$B_{1}C$所成的角是$90^{\circ}$。
其中正确结论的序号是①②③。

答案： 21.①②③ [解析]连接$A_{1}H,BH,DH$。因为$AB=AD=AA_{1},AH\perp$平面$A_{1}BD$，所以$Rt\triangle ABH\congRt\triangle ADH\congRt\triangle AA_{1}H$，所以$HB=HD=HA_{1}$。又因为$\triangle A_{1}BD$是等边三角形，所以$H$是$\triangle A_{1}BD$的中心，所以①正确。
在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，$A_{1}B_{1}// CD$，且$A_{1}B_{1}=CD$，所以四边形$A_{1}B_{1}CD$是平行四边形，所以$B_{1}C// A_{1}D$。又因为$A_{1}D\subset$平面$A_{1}BD,B_{1}C\not\subset$平面$A_{1}BD$，所以$B_{1}C//$平面$A_{1}BD$。同理可证$B_{1}D_{1}//$平面$A_{1}BD$。又因为$B_{1}C\cap B_{1}D_{1}=B_{1},B_{1}C,B_{1}D_{1}\subset$平面$CB_{1}D_{1}$，所以平面$CB_{1}D_{1}//$平面$A_{1}BD$。又因为$AH\perp$平面$A_{1}BD$，所以$AH\perp$平面$CB_{1}D_{1}$，所以②正确。
连接$AD_{1},BC_{1}$。因为四边形$BCC_{1}B_{1}$是正方形，所以$B_{1}C\perp BC_{1}$。因为$AB\perp$平面$BCC_{1}B_{1},B_{1}C\subset$平面$BCC_{1}B_{1}$，所以$B_{1}C\perp AB$。又因为$BC_{1}\cap AB=B,BC_{1},AB\subset$平面$ABCD_{1}$，所以$B_{1}C\perp$平面$ABCD_{1}$。又因为$AC_{1}\subset$平面$ABCD_{1}$，所以$AC_{1}\perp B_{1}C$，所以直线$AC_{1}$与$B_{1}C$所成的角是$90^{\circ}$，所以③正确。
易错警示：本题容易忽视利用三角形全等的知识证明$HB=HD=HA_{1}$，认为①错误；也容易忽视“若$\alpha//\beta,l\perp\alpha$，则$l\perp\beta$”，认为②错误；还容易在利用线面垂直证明线线垂直时出错，认为③错误。

22. [山西长治2025高一月考]已知$m$，$n$为异面直线，$m \perp$平面$\alpha$，$n \perp$平面$\beta$，直线$l$满足$l \perp m$，$l \perp n$，$l \not\subset \alpha$，$l \not\subset \beta$，则(D)

A.$\alpha // \beta$且$l // \alpha$
B.$\alpha \perp \beta$且$l \perp \beta$
C.$\alpha$与$\beta$相交，且交线与$l$垂直
D.$\alpha$与$\beta$相交，且交线与$l$平行

答案： 22.D [解析]若$\alpha//\beta$，则由$m\perp$平面$\alpha,n\perp$平面$\beta$，可得$m// n$，这与$m,n$是异面直线矛盾，故$\alpha$与$\beta$相交。
设$\alpha\cap\beta=a$，过空间内一点$P$，作$m'// m,n'// n$，则$m'$与$n'$相交，设$m'$与$n'$确定的平面为$\gamma$。因为$l\perp m,l\perp n$，所以$l\perp m',l\perp n'$，所以$l\perp\gamma$。
因为$m\perp\alpha,n\perp\beta$，所以$m'\perp\alpha,n'\perp\beta$，所以$a\perp m',a\perp n'$，所以$a\perp\gamma$。
又因为$l\not\subset\alpha,l\not\subset\beta$，所以$l$与$a$不重合，所以$l// a$，所以$l//\alpha,l//\beta$。
易错警示：解答本题时，容易忽视$\alpha//\beta$时，可由条件推出$m// n$，与$m,n$为异面直线矛盾，导致错选A。也容易忽视构造辅助平面$\gamma$，无法利用线面垂直的性质证明线线平行，导致错选C。

23. [清华大学2024强基计划]在四面体$V - ABC$中，$VA = VB = 2\sqrt{2}$，$VC = 3$，$CA = CB = 4$，则$CA$与$VB$所成角的余弦值的取值范围为$[0,\frac{19\sqrt{2}}{36}]$。

答案：
23.$[0,\frac{19\sqrt{2}}{36}]$ [解析]如图，取$P,Q$分别为$VC,AB$的中点，连接$PA,PB,PQ$，
　　　　　　　　　
在$\triangle VBC$中，由余弦定理得$\cos\angle VCB=\frac{3^{2}+4^{2}-(2\sqrt{2})^{2}}{2×3×4}=\frac{17}{24}$，
则$PB=\sqrt{\frac{9}{4}+16-2×\frac{3}{2}×4×\frac{17}{24}}=\frac{\sqrt{39}}{2}$，易证$\triangle VAC\cong\triangle VBC$，所以$PA=PB=\frac{\sqrt{39}}{2}$，在$\triangle ABP$中，$PQ＜PA=\frac{\sqrt{39}}{2}$。
过点$B$作$BH\perp VC$于$H$，设$HP=x$，则$VB^{2}-VH^{2}=BC^{2}-HC^{2}$，即$BC^{2}-VB^{2}=HC^{2}-VH^{2}$，得$8=6x$，解得$x=\frac{4}{3}$。
连接$VQ,CQ,QH$，因为$VA=VB,CA=CB,Q$为$AB$的中点，所以$VQ\perp AB,CQ\perp AB$。
因为$VQ\cap CQ=Q,VQ,CQ\subset$平面$VCQ$，所以$AB\perp$平面$VCQ$。
又$VC\subset$平面$VCQ$，所以$VC\perp AB$。
又$AB\cap BH=B,AB,BH\subset$平面$BHQ$，所以$VC\perp$平面$BHQ$。
因为$QH\subset$平面$BHQ$，所以$QH\perp VC$，所以$PQ＞HP=\frac{4}{3}$。
取$BC$的中点$M$，连接$PM,QM$，则$PM// VB,QM// CA$，所以$CA$与$VB$所成的角即为$\angle PMQ$(或其补角)，
则$\cos\angle PMQ=\frac{PM^{2}+MQ^{2}-PQ^{2}}{2PM· MQ}=\frac{2+4-PQ^{2}}{4\sqrt{2}}=\frac{6-PQ^{2}}{4\sqrt{2}}$。
由$\frac{4}{3}＜PQ＜\frac{\sqrt{39}}{2}$知$\frac{16}{9}＜PQ^{2}＜\frac{39}{4}$，于是$-\frac{15\sqrt{2}}{32}＜\cos\angle PMQ＜\frac{19\sqrt{2}}{36}$。
因为异面直线所成角的取值范围为$(0,\frac{\pi}{2}]$，所以$CA$与$VB$所成角的余弦值的取值范围为$[0,\frac{19\sqrt{2}}{36})$。
避坑：注意异面直线所成角的范围这个隐含条件，否则易致所求范围扩大。