《2026年高中必刷题高中数学必修第二册人教版》

问题 1 观察黑板面、桌面、门面等，生活中的平面与几何里所说的“平面”有何异同？

答案： 提示 生活中的平面是比较平整、有限的。几何中的“平面”是从生活的常见物体中抽象、概括出来的，是理想的、绝对平整的、无限延展的，无大小、厚薄之分，是不可度量的，是不加定义的原始概念。总结起来，平面应具备如下特点：
(1) 平面是平的；
(2) 平面是没有厚度的；
(3) 平面是无限延展的；
(4) 平面是由空间点、线组成的无限集合；
(5) 平面内有无数个点，无数条直线。

问题 2 类比集合中的符号表示，点、线、面之间的位置关系如何表示？

答案：
提示
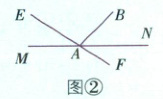
(1) 直线可以看作由无数个点组成的集合，故点与直线的关系是元素与集合的关系，用“∈”或“∉”表示。如图①，点 A 在直线 a 上，记作 A ∈ a；点 B 不在直线 a 上，记作 B ∉ a。
(2) 平面也可以看作点的集合，故点与平面的关系是元素与集合的关系，用“∈”或“∉”表示。如图②，点 A 在平面 α 内，记作 A ∈ α；点 B 不在平面 α 内，记作 B ∉ α。
(3) 直线和平面都可以看成点的集合，它们之间的关系可以看作集合与集合的关系，故用“⊂”或“⊄”表示。见拓展。

问题 3 如何理解基本事实 1，2，3？其作用是什么？

答案：
提示 基本事实 1 的内容关系到“确定”平面的条件。如图：

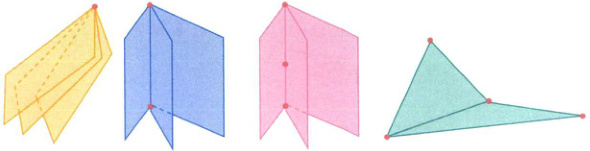
过一点、两点或者同一直线上的三点可以有无数个平面，任给不在同一条直线上的四个点，不一定有一个平面同时过这四个点，故“过不在一条直线上的三点”至关重要。“有且只有一个”的含义：“有”是说图形存在，“只有一个”说明图形唯一。
基本事实 1：一是确定平面以及判断两个平面重合的依据，二是证明点、线共面的依据，三是作截面、辅助平面的依据。
基本事实 2：反映了直线和平面的关系，一是判断直线是否在平面内，二是判断点是否在平面内。
基本事实 3：指出了两个平面的位置关系，进一步反映了平面的延展性。其作用有三个，一是作为判定两个平面相交的依据，只要两个不重合的平面有一个公共点，就可以判定这两个平面必相交于过这个点的公共直线。二是可以判定点在直线上，若点是某两个平面的公共点，直线是这两个平面的公共直线，则点在这条直线上。三是证明点共线或线共点问题。