2026年高中必刷题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年高中必刷题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [安徽合肥 2025 高 - 质量调研] 如图,点 $ N $ 为正方形 $ ABCD $ 的中心,点 $ E $ 在平面 $ ABCD $ 外,$ M $ 是线段 $ ED $ 的中点,则下列各选项中两条直线不是异面直线的为(

A.$ AB $ 与 $ DE $
B.$ BC $ 与 $ EN $
C.$ CD $ 与 $ BM $
D.$ BM $ 与 $ EN $
D
)
A.$ AB $ 与 $ DE $
B.$ BC $ 与 $ EN $
C.$ CD $ 与 $ BM $
D.$ BM $ 与 $ EN $
答案:
1.D 【解析】在正方形ABCD中,AB//CD,所以D在平面ABCD内,D不在直线AB上,又E不在平面ABCD内,所以AB与DE异面;因为BC⊂平面ABCD,N在平面ABCD内,N不在直线BC上,又E不在平面ABCD内,所以BC与EN异面;因为CD⊂平面ABCD,B在平面ABCD内,B不在直线CD上,又M不在平面ABCD内,所以CD与BM异面;

连接BD,BE,MN,因为点N为正方形ABCD的中心,又M是线段ED的中点,所以MN//BE,所以B,M,N,E在平面BDE内,所以BM与EN不是异面直线.故选D.
1.D 【解析】在正方形ABCD中,AB//CD,所以D在平面ABCD内,D不在直线AB上,又E不在平面ABCD内,所以AB与DE异面;因为BC⊂平面ABCD,N在平面ABCD内,N不在直线BC上,又E不在平面ABCD内,所以BC与EN异面;因为CD⊂平面ABCD,B在平面ABCD内,B不在直线CD上,又M不在平面ABCD内,所以CD与BM异面;

连接BD,BE,MN,因为点N为正方形ABCD的中心,又M是线段ED的中点,所以MN//BE,所以B,M,N,E在平面BDE内,所以BM与EN不是异面直线.故选D.
2. 教材变式 (多选) [河南安阳 2024 高一月考] 如图是一个正方体的展开图,将它还原为正方体之后,下列结论正确的有(
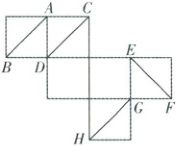
A.$ HG // CD $
B.$ CD $ 与 $ EF $ 异面
C.$ EF $ 与 $ AB $ 异面
D.$ GH // AB $
AC
)
A.$ HG // CD $
B.$ CD $ 与 $ EF $ 异面
C.$ EF $ 与 $ AB $ 异面
D.$ GH // AB $
答案:
2.AC 【解析】根据正方体的展开图画出还原的正方体如图所示.

可以得到HG//CD,CD与EF相交,EF与AB异面,GH与AB相交.故选AC.
链接教材 本题是教材第132页第9题改编的选择题,考查正方体的展开图和空间中直线的位置关系.判断两条直线是否是异面直线,第一:两条直线平行或相交,则两条直线共面,第二:若一条直线与一个平面相交于一点,那么这条直线与这个平面内不经过该点的直线是异面直线,这是判断两条直线是否是异面直线的方法,要根据题目所提供的线线、线面关系准确地作出判断.
2.AC 【解析】根据正方体的展开图画出还原的正方体如图所示.

可以得到HG//CD,CD与EF相交,EF与AB异面,GH与AB相交.故选AC.
链接教材 本题是教材第132页第9题改编的选择题,考查正方体的展开图和空间中直线的位置关系.判断两条直线是否是异面直线,第一:两条直线平行或相交,则两条直线共面,第二:若一条直线与一个平面相交于一点,那么这条直线与这个平面内不经过该点的直线是异面直线,这是判断两条直线是否是异面直线的方法,要根据题目所提供的线线、线面关系准确地作出判断.
3. [广东清远 2025 高一联考] 已知 $ a,b $ 是两条不同的直线,$ \alpha $ 是一个平面,则下列命题中,为真命题的是(
A.若 $ a \subset \alpha,b \not\subset \alpha $,则 $ a $ 与 $ b $ 必异面
B.若点 $ A \notin \alpha $,点 $ B \notin \alpha $,则直线 $ AB // \alpha $
C.若 $ a // \alpha,b \subset \alpha $,则 $ a // b $
D.若点 $ A \in \alpha $,点 $ B \notin \alpha $,则直线 $ AB $ 与 $ \alpha $ 相交
D
)A.若 $ a \subset \alpha,b \not\subset \alpha $,则 $ a $ 与 $ b $ 必异面
B.若点 $ A \notin \alpha $,点 $ B \notin \alpha $,则直线 $ AB // \alpha $
C.若 $ a // \alpha,b \subset \alpha $,则 $ a // b $
D.若点 $ A \in \alpha $,点 $ B \notin \alpha $,则直线 $ AB $ 与 $ \alpha $ 相交
答案:
3.D 【解析】对于A,若a⊂α,b⊄α,则a与b平行或相交或异面,故A为假命题;对于B,若点A∉α,点B∉α,则直线AB//平面α或直线AB与平面α相交,故B为假命题;对于C,若a//α,b⊂α,则a与b平行或异面,故C为假命题;对于D,若点A∈α,点B∉α,则直线AB与平面α相交,故D为真命题.故选D.
4. [浙江衢州 2024 高二质量检测] 已知直线 $ m $ 和平面 $ \alpha $,则“$ m \not\subset \alpha $”是“直线 $ m $ 与平面 $ \alpha $ 无公共点”的(
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
B
)A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:
4.B 【解析】因为m⊄α包含m//α和直线m与平面α相交两种情况,因此若m⊄α,
⟹坑:容易忽略m与平面α相交这种情况
则直线m可以与平面α无公共点,也可以与平面α有一个公共点,因此“m⊄α”是“直线m与平面α无公共点”的必要不充分条件.故选B.
⟹坑:容易忽略m与平面α相交这种情况
则直线m可以与平面α无公共点,也可以与平面α有一个公共点,因此“m⊄α”是“直线m与平面α无公共点”的必要不充分条件.故选B.
5. 教材变式 若三个平面两两相交,有三条交线,则下列说法正确的是(
A.三条交线为异面直线
B.三条交线两两平行
C.三条交线交于一点
D.三条交线两两平行或交于一点
D
)A.三条交线为异面直线
B.三条交线两两平行
C.三条交线交于一点
D.三条交线两两平行或交于一点
答案:
5.D 【解析】三个平面两两相交,有三条交线,则这三条交线两两平行或交于一点.三条交线两两平行,如三棱柱的三个侧面两两相交,交线是三棱柱的三条侧棱,这三条侧棱是互相平行的.三条交线交于一点,如长方体的三个相邻的面两两相交,交线交于长方体的一个顶点.故选D.
链接教材 本题是教材第132页第7题改编的选择题,考查多个平面两两相交时交线的位置关系.做题时可以从两个角度入手:一是借助熟悉的简单几何体作为参考去直观感受,比如三棱柱和三棱锥;二是借助三个基本事实展开逻辑推理.
链接教材 本题是教材第132页第7题改编的选择题,考查多个平面两两相交时交线的位置关系.做题时可以从两个角度入手:一是借助熟悉的简单几何体作为参考去直观感受,比如三棱柱和三棱锥;二是借助三个基本事实展开逻辑推理.
6. (多选) [河南周口 2025 高一诊断性考试] 下列说法正确的是(
A.三个平面最多可以把空间分成 8 部分
B.若直线 $ a \subset $ 平面 $ \alpha $,直线 $ b \subset $ 平面 $ \beta $,则“$ a $ 与 $ b $ 相交”的充要条件是“$ \alpha $ 与 $ \beta $ 相交”
C.若 $ \alpha \cap \beta = l $,直线 $ a \subset $ 平面 $ \alpha $,直线 $ b \subset $ 平面 $ \beta $,且 $ a \cap b = P $,则 $ P \in l $
D.若 $ n $ 条直线中任意两条共面,则它们共面
AC
)A.三个平面最多可以把空间分成 8 部分
B.若直线 $ a \subset $ 平面 $ \alpha $,直线 $ b \subset $ 平面 $ \beta $,则“$ a $ 与 $ b $ 相交”的充要条件是“$ \alpha $ 与 $ \beta $ 相交”
C.若 $ \alpha \cap \beta = l $,直线 $ a \subset $ 平面 $ \alpha $,直线 $ b \subset $ 平面 $ \beta $,且 $ a \cap b = P $,则 $ P \in l $
D.若 $ n $ 条直线中任意两条共面,则它们共面
答案:
6.AC 【解析】A选项,当三个平面交于一点时,最多可以把空间分成8部分,此时可看成墙角的三个平面,故A选项正确;B选项,“α与β相交”推不出“a与b相交”,也可能a//b,故B选项错误;C选项,因为α∩β=l,所以直线l是α与β的交线,因为a⊂α,b⊂β,且a∩b=P,则P⊂α,P⊂β,则P∈l,故C选项正确;D选项,正方体的侧棱任意两条都共面,但这4条侧棱却不共面,故D选项错误.故选AC.
7. [贵州 2025 高一月考] 已知平面 $ \alpha,\beta $ 和直线 $ a,b,c $,且 $ a // b // c,a \subset \alpha,b \subset \beta,c \subset \beta $,则 $ \alpha $ 与 $ \beta $ 的位置关系是
平行或相交
。
答案:
7.平行或相交 【解析】b//c,b⊂β,c⊂β,当α与β相交或平行时,都能找到a//b//c且a⊂α,如图.

7.平行或相交 【解析】b//c,b⊂β,c⊂β,当α与β相交或平行时,都能找到a//b//c且a⊂α,如图.

8. 下列说法正确的是
①若两直线无公共点,则两直线平行;
②两直线若不是异面直线,则必相交或平行;
③过平面外一点与平面内一点的直线,与平面内的任一直线均构成异面直线;
④和两条异面直线都相交的两直线必是异面直线。
②
。(写出所有正确说法的序号)①若两直线无公共点,则两直线平行;
②两直线若不是异面直线,则必相交或平行;
③过平面外一点与平面内一点的直线,与平面内的任一直线均构成异面直线;
④和两条异面直线都相交的两直线必是异面直线。
答案:
8.② 【解析】对于①,两直线无公共点,可能平行,也可能异面,故①错误;对于②,由两直线的位置关系知②正确;对于③,过平面外一点与平面内一点的直线,与平面内经过线面交点的直线是相交直线,而不是异面直线,故③错误;对于④,和两条异面直线都相交的两直线可能是异面直线,也可能是相交直线,故④错误.
易错警示 异面直线的定义是不同在任何一个平面内的两条直线,容易理解片面出现误选的情况,以及对问题考虑不全面作出错误判断.
易错警示 异面直线的定义是不同在任何一个平面内的两条直线,容易理解片面出现误选的情况,以及对问题考虑不全面作出错误判断.
9. 已知 $ \alpha,\beta $ 为两个不同的平面,$ a,b $ 为两条不同的直线,给出下列说法:
①若 $ \alpha // \beta,a \subset \alpha,b \subset \beta $,则 $ a // b $;
②若 $ \alpha // \beta,a \subset \alpha,b \subset \beta $,则 $ a $ 与 $ b $ 是异面直线;
③若 $ \alpha // \beta,a \subset \alpha,b \subset \beta $,则 $ a $ 与 $ b $ 平行或异面;
④若 $ \alpha \cap \beta = b,a \subset \alpha $,则 $ a $ 与 $ \beta $ 一定相交。
其中正确的是
①若 $ \alpha // \beta,a \subset \alpha,b \subset \beta $,则 $ a // b $;
②若 $ \alpha // \beta,a \subset \alpha,b \subset \beta $,则 $ a $ 与 $ b $ 是异面直线;
③若 $ \alpha // \beta,a \subset \alpha,b \subset \beta $,则 $ a $ 与 $ b $ 平行或异面;
④若 $ \alpha \cap \beta = b,a \subset \alpha $,则 $ a $ 与 $ \beta $ 一定相交。
其中正确的是
③
。(写出所有正确说法的序号)
答案:
9.③ 【解析】分别在两个平行平面内的两条直线没有公共点,则这两条直线可能平行,也可能异面,所以①②错误,③正确;④中α与β也可能平行,所以④错误.
易错警示 对没有公共点的两条直线的位置关系考虑不全面而误选①或②.解决这类问题的基本思路:一是逐个判断,利用空间线线、线面、面面的位置关系证明正确的结论,寻找反例否定错误的结论;二是结合几何体模型或实际空间位置作出判断,但要注意在应用定理时要准确,考虑问题要全面.
易错警示 对没有公共点的两条直线的位置关系考虑不全面而误选①或②.解决这类问题的基本思路:一是逐个判断,利用空间线线、线面、面面的位置关系证明正确的结论,寻找反例否定错误的结论;二是结合几何体模型或实际空间位置作出判断,但要注意在应用定理时要准确,考虑问题要全面.
查看更多完整答案,请扫码查看


