《2026年高中必刷题高中数学必修第二册人教版》

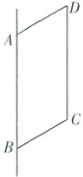
1. [浙江杭州 2025 高一期中]如图，在平行四边形 $ABCD$ 中，$AB = 2$，$BC = 1$，$\angle B = \frac{\pi}{3}$，以 $AB$ 所在直线为轴，其他三边旋转一周所围成的几何体的表面积是(B)

A.$2\sqrt{3}\pi$
B.$3\sqrt{3}\pi$
C.$4\sqrt{3}\pi$
D.$\frac{3}{2}\pi$

答案： 1.B [解析]由题意可得，以AB所在直线为轴，其他三边旋转一周所围成的几何体的上部分为圆柱内挖去一个圆锥，下部分为与上部分挖去部分相同的圆锥，圆锥和圆柱的底面圆半径$r = BC × \sin \frac{\pi}{3} = \frac{\sqrt{3}}{2}$，圆柱的高为$CD = AB = 2$，一个圆锥的侧面积为$\pi × \frac{\sqrt{3}}{2} × 1 = \frac{\sqrt{3}}{2}\pi$，圆柱的侧面积为$2\pi × \frac{\sqrt{3}}{2} × 2 = 2\sqrt{3}\pi$，所以该几何体的表面积为2个圆锥的侧面积加一个圆柱的侧面积，为$2 × \frac{\sqrt{3}}{2}\pi + 2\sqrt{3}\pi = 3\sqrt{3}\pi$.故选B.

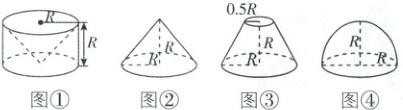
2. 教材变式 祖暅是南北朝时期的伟大科学家，他于 5 世纪末提出体积计算原理，即祖暅原理：“幂势既同，则积不容异”，意思是夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等. 现有以下四个几何体：图①是从圆柱中挖去一个同底等高的圆锥所得的几何体，图②、图③、图④分别是圆锥、圆台和半球，则满足祖暅原理的两个几何体为(D)

A.①②
B.①③
C.②④
D.①④

答案： 2.D [解析]设截面与(下)底面的距离为$h$，则①中截面内圆半径为$h$，则截面圆环的面积为$\pi(R^2 - h^2)$；
②中截面圆的半径为$R - h$，则截面圆的面积为$\pi(R - h)^2$；
③中截面圆的半径为$R - \frac{h}{2}$，则截面圆的面积为$\pi(R - \frac{h}{2})^2$；
④中截面圆的半径为$\sqrt{R^2 - h^2}$，则截面圆的面积为$\pi(R^2 - h^2)$.
所以①④中截面的面积总相等.又①中几何体的高与④中半球的半径相等，所以①④满足祖暅原理.故选D.
链接教材本题是教材第121 - 123页探究与发现“祖暅原理与柱体、锥体的体积”的应用，做题时要紧抓祖暅原理“幂势既同，则积不容异”的两条原则：幂、势相同，即要保证高度相同且任意同高度处截面面积相同.

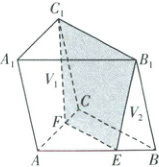
3. [河南信阳高中 2024 高一期中]如图所示，在三棱柱 $ABC - A_1B_1C_1$ 中，若点 $E$，$F$ 分别满足 $\overrightarrow{AE} = \frac{2}{3}\overrightarrow{AB}$，$\overrightarrow{AF} = \frac{2}{3}\overrightarrow{AC}$，平面 $EB_1C_1F$ 将三棱柱分成体积为 $V_1$，$V_2$ 的两部分，则 $V_1:V_2 =$(A)

A.$19:8$
B.$2:1$
C.$17:10$
D.$16:11$

答案： 3.A [解析]$\because \overrightarrow{AE} = \frac{2}{3}\overrightarrow{AB}, \overrightarrow{AF} = \frac{2}{3}\overrightarrow{AC}, \therefore EF // BC, EF = \frac{2}{3}BC, \therefore S_{\triangle AEF} = \frac{4}{9}S_{\triangle ABC}$.
$\because \frac{EF}{B_1C_1} = \frac{AF}{A_1C_1} = \frac{AE}{A_1B_1} = \frac{2}{3}$，
$\therefore$几何体$AEF - A_1B_1C_1$为三棱台.
设三棱柱$ABC - A_1B_1C_1$的高为$h$，
则$V_1 = \frac{1}{3}(S_{\triangle AEF} + \sqrt{S_{\triangle AEF} · S_{\triangle A_1B_1C_1}} + S_{\triangle A_1B_1C_1}) · h$
$= \frac{1}{3}(\frac{4}{9}S_{\triangle ABC} + \frac{2}{3}S_{\triangle ABC} + S_{\triangle ABC}) · h$
$= \frac{19}{27}S_{\triangle ABC} · h = \frac{19}{27}V_{ABC - A_1B_1C_1}$，
$\therefore V_2 = V_{ABC - A_1B_1C_1} - V_1 = \frac{8}{27}V_{ABC - A_1B_1C_1}$，
$\therefore V_1 : V_2 = 19 : 8$.故选A.
名师点拨几何体求表面积、体积的转化策略
①“转”：指的是转换底面与高，将原来不容易求面积的底面转换为容易求面积的底面，或将原来不容易看出的高转换为容易看出并容易求解的高.②“拆”：指的是将一个不规则的几何体拆成几个简单的几何体，便于计算.③“拼”：指的是将小几何体嵌入一个大几何体中，如将三棱锥补成三棱柱，将三棱柱补成四棱柱，将台体补成锥体，这些都是拼补的方法.

4. 已知三棱锥 $P - ABC$ 的三条侧棱两两互相垂直，且 $AB = \sqrt{5}$，$BC = \sqrt{7}$，$AC = 2$，则此三棱锥的外接球的体积为(B)

A.$\frac{8}{3}\pi$
B.$\frac{8\sqrt{2}}{3}\pi$
C.$\frac{16}{3}\pi$
D.$\frac{32}{3}\pi$

答案： 4.B [解析]由题意，可将三棱锥放入长方体中考虑，则长方体的外接球即为三棱锥的外接球，故球的半径为长方体体对角线的一半，设$PA = x$，则$PB^2 + PC^2 = BC^2 = 7$，所以$5 - x^2 + 4 - x^2 = 7$，解得$x = 1$，故$PA = 1, PB = 2, PC = \sqrt{3}$，所以三棱锥$P - ABC$外接球的半径$R = \frac{\sqrt{1^2 + 2^2 + (\sqrt{3})^2}}{2} = \sqrt{2}$，得球的体积为$\frac{4}{3}\pi R^3 = \frac{8\sqrt{2}\pi}{3}$.故选B.
规律方法补形法是求三棱锥外接球相关问题常用的方法之一，正四面体、四个面都是直角三角形的三棱锥、同一个顶点上的三条棱两两垂直的三棱锥、相对的棱相等的三棱锥都可以补成正方体或者长方体，进而求解.

5. (多选)[吉林省吉林市普通高中 2024 高一期末联考]正三棱锥的底面边长为 3，侧棱长为 $2\sqrt{3}$，则下列叙述正确的是(ABD)

A.正三棱锥的高为 3
B.正三棱锥的斜高为 $\frac{\sqrt{39}}{2}$
C.正三棱锥的体积为 $\frac{27\sqrt{3}}{4}$
D.正三棱锥的侧面积为 $\frac{9\sqrt{39}}{4}$

答案：
5.ABD [解析]如图，设E为等边三角形ADC的中心，F为CD的中点，连接PF，EF，PE，则PE为正三棱锥的高，PF为斜高，又$PF = \sqrt{(2\sqrt{3})^2 - (\frac{3}{2})^2} = \frac{\sqrt{39}}{2}$，$EF = \frac{1}{3} × \frac{3\sqrt{3}}{2} = \frac{\sqrt{3}}{2}$，故$PE = \sqrt{PF^2 - EF^2} = 3$，故A，B正确.正三棱锥的体积为$\frac{1}{3} ×$
巧思：利用正弦定理求出底面$\triangle ACD$外接圆的半径，即$DE = \frac{3}{2\sin \frac{\pi}{3}} = \sqrt{3}$，则可通过$PE = \sqrt{PD^2 - DE^2}$求解
$\frac{\sqrt{3}}{4} × 3^2 = \frac{9\sqrt{3}}{4}$，侧面积为$3 × \frac{1}{2} × 3 × \frac{\sqrt{39}}{2} = \frac{9\sqrt{39}}{4}$，故C错误，D正确.故选ABD.

6. (多选)[浙江余姚 2024 高一期中]已知棱长为 2 的正方体 $ABCD - A_1B_1C_1D_1$ 的棱切球(与正方体的各条棱都相切)为球 $O$，则下列说法正确的是(BCD)

A.球 $O$ 的体积为 $\frac{4}{3}\pi$
B.球 $O$ 内接圆柱的侧面积的最大值为 $4\pi$
C.球 $O$ 在正方体外部的体积小于 $\frac{4}{3}(2\sqrt{2} - 1)\pi$
D.球 $O$ 在正方体外部的面积大于 $6\sqrt{4 - 2\sqrt{2}}\pi$

答案：
6.BCD [解析]对于A，依题意，得棱切球的半径为$\sqrt{2}$，则球O的体积为$\frac{4}{3}\pi × (\sqrt{2})^3 = \frac{8\sqrt{2}}{3}\pi$，A错误；
对于B，记球O的内接圆柱的底面半径为$r$，则内接圆柱的高为$\sqrt{(2\sqrt{2})^2 - (2r)^2} = \sqrt{8 - 4r^2}$，则内接圆柱的侧面积$S = 2\pi r · \sqrt{8 - 4r^2} = 4\pi \sqrt{r^2 · (2 - r^2)} \leq 4\pi · \frac{r^2 + 2 - r^2}{2} = 4\pi$，当且仅当$r = 1$时等号成立，故球O的内接圆柱的侧面积的最大值为$4\pi$，B正确；
对于C，球O在正方体外部的体积小于球O的体积与正方体内切球的体积之差，即$\frac{8\sqrt{2}}{3}\pi - \frac{4}{3}\pi × 1^3 = \frac{4}{3}(2\sqrt{2} - 1)\pi$，C正确；
对于D，球O在正方体外部的面积等于正方体外6个球冠的表面积，每一个球冠的表面积大于这个球冠中内接圆锥的侧面积，则内接圆锥的底面半径为1，高为$\sqrt{2} - 1$，则内接圆锥的母线长为$\sqrt{1^2 + (\sqrt{2} - 1)^2} = \sqrt{4 - 2\sqrt{2}}$，则内接圆锥的侧面积为$\pi × 1 × \sqrt{4 - 2\sqrt{2}} = \sqrt{4 - 2\sqrt{2}}\pi$，所以6个球冠的表面积大于$6\sqrt{4 - 2\sqrt{2}}\pi$，D正确.


故选BCD.
名师点拨D项中球O在正方体外部的面积等于正方体外6个球冠的表面积，每一个球冠的表面积大于这个球冠中内接圆锥的侧面积.

7. [广东东莞 2025 高一期中]已知正六棱柱 $ABCDEF - A_1B_1C_1D_1E_1F_1$ 的各个顶点都在半径为 $R$ 的球面上，一个能放进该正六棱柱内部的最大的球的半径为 $r$. 若 $AB = 2$，则当 $\frac{R}{r}$ 最小时，该正六棱柱的体积为36.

答案：
7.36 [解析]设正六边形ABCDEF的中心为M，则点M与正六边形ABCDEF的任意一条边均构成等边三角形，因此点M到各边的距离均为等边三角形的高，即为$2\sin 60° = \sqrt{3}$.
不妨设该正六棱柱的高为$h$，则$r = \min\{\sqrt{3}, \frac{h}{2}\}$.
易得该正六棱柱的外接球半径为$R = \sqrt{(\frac{h}{2})^2 + 2^2} = \frac{\sqrt{h^2 + 16}}{2}$
当$h ＜ 2\sqrt{3}$时，$r = \frac{h}{2}, \frac{R}{r} = \frac{\sqrt{h^2 + 16}}{h} = \sqrt{1 + \frac{16}{h^2}} ＞ \sqrt{1 + \frac{16}{12}} = \frac{\sqrt{21}}{3}$；
当$h \geq 2\sqrt{3}$时，$r = \sqrt{3}, \frac{R}{r} = \frac{\sqrt{h^2 + 16}}{2\sqrt{3}} \geq \frac{\sqrt{12 + 16}}{2\sqrt{3}} = \frac{\sqrt{21}}{3}$，
所以$h = 2\sqrt{3}$时，$\frac{R}{r}$取得最小值$\frac{\sqrt{21}}{3}$.
又底面上一个等边三角形的面积为$\frac{1}{2} × 2^2 × \sin 60° = \sqrt{3}$，所以正六棱柱底面的面积为$6\sqrt{3}$，
则此时该正六棱柱的体积为$6\sqrt{3} × 2\sqrt{3} = 36$.