2026年高中必刷题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年高中必刷题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [福建福州 2025 高一期中]下列说法正确的是(
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有 9 条侧棱,9 个侧面,侧面均为平行四边形
D
)A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有 9 条侧棱,9 个侧面,侧面均为平行四边形
答案:
1. D 【解析】有两个面平行,其余各面是四边形,且每相邻两个四边形的公共边都相互平行的几何体叫棱柱,满足A选项或B选项描述的一种几何体如图所示,故A,B都不正确.

黑板:判断时除了根据定义,也可尝试能否仅用已知条件举出反例
各侧面都是正方形的四棱柱,上下底面可能是菱形,故C不正确.
根据棱柱的定义可知九棱柱有9条侧棱,9个侧面,侧面均为平行四边形,故D正确.故选D.
规律方法 判断棱柱的关键
(1)紧抓定义:有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行;
(2)注意空间位置关系:相互平行的两个面不一定是上下相对,也可以左右或前后相对,只要满足这两个面平行即可.
1. D 【解析】有两个面平行,其余各面是四边形,且每相邻两个四边形的公共边都相互平行的几何体叫棱柱,满足A选项或B选项描述的一种几何体如图所示,故A,B都不正确.

黑板:判断时除了根据定义,也可尝试能否仅用已知条件举出反例
各侧面都是正方形的四棱柱,上下底面可能是菱形,故C不正确.
根据棱柱的定义可知九棱柱有9条侧棱,9个侧面,侧面均为平行四边形,故D正确.故选D.
规律方法 判断棱柱的关键
(1)紧抓定义:有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行;
(2)注意空间位置关系:相互平行的两个面不一定是上下相对,也可以左右或前后相对,只要满足这两个面平行即可.
2. (多选)[浙江宁波 2024 高一期中]下列命题中为假命题的是(
A.长方体是四棱柱,直四棱柱是长方体
B.棱柱中至少有两个面的形状完全相同
C.有两个侧面是矩形的四棱柱是直四棱柱
D.正四棱柱是平行六面体
AC
)A.长方体是四棱柱,直四棱柱是长方体
B.棱柱中至少有两个面的形状完全相同
C.有两个侧面是矩形的四棱柱是直四棱柱
D.正四棱柱是平行六面体
答案:
2. AC 【解析】对于选项A,当底面不是矩形的时候,直四棱柱非长方体,A为假命题;对于选项B,棱柱的两个底面全等,则棱柱中至少有两个面的形状完全相同,B为真命题;对于选项C,有两个侧面是矩形的四棱柱可以是两对称面为矩形的平行六面体,C为假命题;D选项,正四棱柱是平行六面体,D为真命题.故选AC.
3. [山西大学附属中学 2025 高一期中]如图所示,在三棱台 $ A'B'C'-ABC $ 中,截去三棱锥 $ A'-ABC $,则剩余部分是(
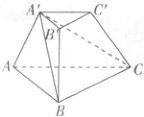
A.三棱锥
B.四棱锥
C.三棱柱
D.组合体
B
)
A.三棱锥
B.四棱锥
C.三棱柱
D.组合体
答案:
3. B 【解析】三棱台A'B'C'−ABC中,沿平面A'BC截去三棱锥A'−ABC,剩余的部分是以A'为顶点,四边形BCC'B'为底面的四棱锥A'−BCC'B'.故选B.
4. (多选)[广东肇庆 2024 高一期中]下列说法中正确的有(
A.正四面体是正三棱锥
B.棱锥的侧面是全等的三角形
C.正三棱锥是正四面体
D.延长棱台所有侧棱,它们会交于一点
AD
)A.正四面体是正三棱锥
B.棱锥的侧面是全等的三角形
C.正三棱锥是正四面体
D.延长棱台所有侧棱,它们会交于一点
答案:
4. AD 【解析】A选项,正四面体的四个面都是等边三角形,是正三棱锥,A正确;
B选项,棱锥的侧面是三角形,不一定全等,B错误;
C选项,正三棱锥的侧棱长和底面边长不一定相等,C错误;
D选项,根据棱台的定义可知,延长棱台所有侧棱,它们会交于一点,D正确.故选AD.
B选项,棱锥的侧面是三角形,不一定全等,B错误;
C选项,正三棱锥的侧棱长和底面边长不一定相等,C错误;
D选项,根据棱台的定义可知,延长棱台所有侧棱,它们会交于一点,D正确.故选AD.
5. 教材变式(多选)[河南郑州 2024 高一期中]下列说法中,不正确的是(
A.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
B.有一个面是多边形,其余各面都是三角形的几何体是棱锥
C.棱锥至少有 6 条棱
D.若棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是正三棱锥
AB
)A.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
B.有一个面是多边形,其余各面都是三角形的几何体是棱锥
C.棱锥至少有 6 条棱
D.若棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是正三棱锥
答案:
5. AB 【解析】对于A,有两个面互相平行,其余四个面都是等腰梯形的六面体不一定是棱台,如图①.只有当四个等腰梯形的腰延长后交于一点,这个六面体才是棱台,故A错误

对于B,有一个面是多边形,其余各面都是三角形的几何体不一定是棱锥,如图②,故B错误

对于C,三棱锥是棱数最少的棱锥,有6条棱,故C正确.
对于D,棱锥的侧棱长与底面多边形的边长相等,若底面是正三角形,则此棱锥是正三棱锥,故D正确.故选AB.
链接教材 本题A选项是教材第106页习题8.1第10题的变式.判断几何体的类型时要对概念和性质把握完整,注意棱台不仅要满足两个面互相平行,其余各面都是梯形,还需要满足侧棱延长后交于一点.
特别注意 有一个面是多边形,其余各面都是三角形的几何体不一定为棱锥,如第5题解析中图②.棱锥还需满足各侧面有且只有一个公共顶点.
5. AB 【解析】对于A,有两个面互相平行,其余四个面都是等腰梯形的六面体不一定是棱台,如图①.只有当四个等腰梯形的腰延长后交于一点,这个六面体才是棱台,故A错误

对于B,有一个面是多边形,其余各面都是三角形的几何体不一定是棱锥,如图②,故B错误

对于C,三棱锥是棱数最少的棱锥,有6条棱,故C正确.
对于D,棱锥的侧棱长与底面多边形的边长相等,若底面是正三角形,则此棱锥是正三棱锥,故D正确.故选AB.
链接教材 本题A选项是教材第106页习题8.1第10题的变式.判断几何体的类型时要对概念和性质把握完整,注意棱台不仅要满足两个面互相平行,其余各面都是梯形,还需要满足侧棱延长后交于一点.
特别注意 有一个面是多边形,其余各面都是三角形的几何体不一定为棱锥,如第5题解析中图②.棱锥还需满足各侧面有且只有一个公共顶点.
6. 如图是一个正方体的表面展开图,则图中“九”在正方体中的对面是(

A.县
B.市
C.联
D.考
B
)
A.县
B.市
C.联
D.考
答案:
6. B 【解析】把正方体还原后如图所示,

则上面是九,下面是市,左面是县,右面是联,前面是考,后面是区,故选B.
6. B 【解析】把正方体还原后如图所示,

则上面是九,下面是市,左面是县,右面是联,前面是考,后面是区,故选B.
7. [吉林长春吉大附中实验学校 2025 高一期中]如图所示,在直三棱柱 $ ABC - A_1B_1C_1 $ 中,$ AB = BC = 2 $,$ BB_1 = 2\sqrt{2} $,$ \angle ABC = 90° $,$ E $,$ F $ 分别是 $ AA_1 $,$ B_1C_1 $ 的中点,沿棱柱表面从 $ E $ 到 $ F $ 的最短路径长为(
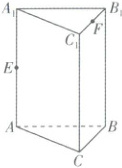
A.$ \sqrt{11} $
B.$ \sqrt{7 + 2\sqrt{2}} $
C.3
D.$ \sqrt{7 + \sqrt{2}} $
C
)
A.$ \sqrt{11} $
B.$ \sqrt{7 + 2\sqrt{2}} $
C.3
D.$ \sqrt{7 + \sqrt{2}} $
答案:
7. C 【解析】若从E到F经过棱A₁B₁,则沿棱A₁B₁展开如图①,
悟:根据经过的不同棱考虑展开图过E作EG⊥BB₁于G,则EG=AB=2,FG=1 + √2,
故EF = √(2² + (1 + √2)²) = √(7 + 2√2).

若从E到F经过棱BB₁,则沿棱BB₁展开如图②,A₁E = √2,A₁F = 3,则EF = √((√2)² + 3²) = √11.

若从E到F经过棱CC₁,则沿棱CC₁展开如图③,因为AB = BC = 2,∠ABC = 90°,
所以AC = √(2² + 2²) = 2√2,
A₁E = √2,A₁F = 2√2 + 1,则EF = √(2 + (2√2 + 1)²) = √(11 + 4√2).

若从E到F经过棱A₁C₁,则沿棱A₁C₁展开如图④,连接AC₁,由题意,△A₁B₁C₁为等腰直角三角形,四边形ACC₁A₁为正方形,故△A₁AC₁为等腰直角三角形,故四边形A₁B₁C₁A为直角梯形.
又A₁B₁ = 2,AC₁ = √((2√2)² + (2√2)²) = 4,故EF = 1/2×(2 + 4) = 3.

又3 = √9 < √(7 + 2√2) < √11 < √(11 + 4√2),所以沿棱柱表面从E到F的最短路径长为3.故选C.
规律方法 求解多面体的表面两点间最短距离时要注意根据几何体的特征,沿着不同的棱将几何体展开后,根据展开图的特征确定最小值.
7. C 【解析】若从E到F经过棱A₁B₁,则沿棱A₁B₁展开如图①,
悟:根据经过的不同棱考虑展开图过E作EG⊥BB₁于G,则EG=AB=2,FG=1 + √2,
故EF = √(2² + (1 + √2)²) = √(7 + 2√2).

若从E到F经过棱BB₁,则沿棱BB₁展开如图②,A₁E = √2,A₁F = 3,则EF = √((√2)² + 3²) = √11.

若从E到F经过棱CC₁,则沿棱CC₁展开如图③,因为AB = BC = 2,∠ABC = 90°,
所以AC = √(2² + 2²) = 2√2,
A₁E = √2,A₁F = 2√2 + 1,则EF = √(2 + (2√2 + 1)²) = √(11 + 4√2).

若从E到F经过棱A₁C₁,则沿棱A₁C₁展开如图④,连接AC₁,由题意,△A₁B₁C₁为等腰直角三角形,四边形ACC₁A₁为正方形,故△A₁AC₁为等腰直角三角形,故四边形A₁B₁C₁A为直角梯形.
又A₁B₁ = 2,AC₁ = √((2√2)² + (2√2)²) = 4,故EF = 1/2×(2 + 4) = 3.

又3 = √9 < √(7 + 2√2) < √11 < √(11 + 4√2),所以沿棱柱表面从E到F的最短路径长为3.故选C.
规律方法 求解多面体的表面两点间最短距离时要注意根据几何体的特征,沿着不同的棱将几何体展开后,根据展开图的特征确定最小值.
8. [安徽宿州示范高中 2024 高一期中]现有一块如图所示的三棱锥木料,其中 $ \angle AVB = \angle AVC = \angle BVC = 40° $,$ VA = VB = VC = 6 $,木工师傅打算过点 $ A $ 将木料切成两部分,则截面 $ \triangle AEF $ 周长的最小值为
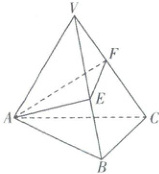
6√3
。
答案:
8. 6√3 【解析】将三棱锥的侧面沿着VA展开,连接A'A,如图所示.

则VA = VA' = 6,∠AVA' = 120°,
由余弦定理可得,AA'² = 6² + 6² - 2×6×6cos120° = 108,则AA' = 6√3,
所以截面△AEF周长的最小值为6√3.
规律方法 解决几何体的表面上连接两点的折线长最短的问题,常转化为求其展开图中相应的点所连线段的长度,即用“化曲为直”的方法将空间问题转化为平面问题.
8. 6√3 【解析】将三棱锥的侧面沿着VA展开,连接A'A,如图所示.

则VA = VA' = 6,∠AVA' = 120°,
由余弦定理可得,AA'² = 6² + 6² - 2×6×6cos120° = 108,则AA' = 6√3,
所以截面△AEF周长的最小值为6√3.
规律方法 解决几何体的表面上连接两点的折线长最短的问题,常转化为求其展开图中相应的点所连线段的长度,即用“化曲为直”的方法将空间问题转化为平面问题.
查看更多完整答案,请扫码查看


