2026年高中必刷题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年高中必刷题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [贵州贵阳 2025 高一月考]向量$\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OM}+\overrightarrow{MB}+\overrightarrow{BC}=$(
A.$\overrightarrow{AC}$
B.$\overrightarrow{AB}$
C.$\overrightarrow{BC}$
D.$\overrightarrow{AM}$
A
)A.$\overrightarrow{AC}$
B.$\overrightarrow{AB}$
C.$\overrightarrow{BC}$
D.$\overrightarrow{AM}$
答案:
1.A 【解析】根据平面向量加法的三角形法则,可得$\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OM}+\overrightarrow{MB}+\overrightarrow{BC}=\overrightarrow{AC}$.故选A.
2. [重庆涪陵五中 2024 高一月考]如图,在平行四边形$ABCD$中,$\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{DA}=$(
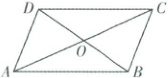
A.$\boldsymbol{0}$
B.$\overrightarrow{OA}$
C.$\overrightarrow{AD}$
D.$\overrightarrow{AC}$
A
)
A.$\boldsymbol{0}$
B.$\overrightarrow{OA}$
C.$\overrightarrow{AD}$
D.$\overrightarrow{AC}$
答案:
2.A 【解析】依题意,$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$,所以
$\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{DA}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{BA}+\overrightarrow{DA}=\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DA}=0$.故选A.
向量运算的交换律同实数运算的交换律
名师点拨 三角形法则与平行四边形法则的记忆口诀:①三角形法则,作平移,首尾连,由起点指终点;②平行四边形法则,作平移,共起点,四边形对角线。三角形法则和平行四边形法则区别有两个:①三角形法则中强调“首尾相接”,平行四边形法则中强调的是“共起点”;②三角形法则适用于所有的两个非零向量求和,而平行四边形法则仅适用于不共线的两个向量求和,三角形法则作出的图形是平行四边形法则作出的图形的一半,当两个向量不共线时,两种加法法则在本质上是一致的。
$\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{DA}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{BA}+\overrightarrow{DA}=\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DA}=0$.故选A.
向量运算的交换律同实数运算的交换律
名师点拨 三角形法则与平行四边形法则的记忆口诀:①三角形法则,作平移,首尾连,由起点指终点;②平行四边形法则,作平移,共起点,四边形对角线。三角形法则和平行四边形法则区别有两个:①三角形法则中强调“首尾相接”,平行四边形法则中强调的是“共起点”;②三角形法则适用于所有的两个非零向量求和,而平行四边形法则仅适用于不共线的两个向量求和,三角形法则作出的图形是平行四边形法则作出的图形的一半,当两个向量不共线时,两种加法法则在本质上是一致的。
3. [广东揭阳一中 2025 高一段考]对于任意一个四边形$ABCD$,下列式子不能化简为$\overrightarrow{BC}$的有(
A.$\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DC}$
B.$\overrightarrow{BD}+\overrightarrow{DA}+\overrightarrow{AC}$
C.$\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DC}$
D.$\overrightarrow{DC}+\overrightarrow{BA}+\overrightarrow{AD}$
C
)A.$\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DC}$
B.$\overrightarrow{BD}+\overrightarrow{DA}+\overrightarrow{AC}$
C.$\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DC}$
D.$\overrightarrow{DC}+\overrightarrow{BA}+\overrightarrow{AD}$
答案:
3.C 【解析】对于A,$\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{BD}+\overrightarrow{DC}=\overrightarrow{BC}$;
对于B,$\overrightarrow{BD}+\overrightarrow{DA}+\overrightarrow{AC}=\overrightarrow{BA}+\overrightarrow{AC}=\overrightarrow{BC}$;
对于C,$\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DC}=\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}$;
对于D,$\overrightarrow{DC}+\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{DC}+\overrightarrow{BD}=\overrightarrow{BD}+\overrightarrow{DC}=\overrightarrow{BC}$.
故选C.
对于B,$\overrightarrow{BD}+\overrightarrow{DA}+\overrightarrow{AC}=\overrightarrow{BA}+\overrightarrow{AC}=\overrightarrow{BC}$;
对于C,$\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DC}=\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}$;
对于D,$\overrightarrow{DC}+\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{DC}+\overrightarrow{BD}=\overrightarrow{BD}+\overrightarrow{DC}=\overrightarrow{BC}$.
故选C.
4. [四川成都树德中学 2024 高一月考]如图,向量$\overrightarrow{AB}=\boldsymbol{a}$,$\overrightarrow{AC}=\boldsymbol{b}$,$\overrightarrow{CD}=\boldsymbol{c}$,则向量$\overrightarrow{BD}$可以表示为(
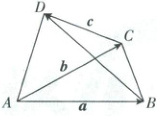
A.$\boldsymbol{a}+\boldsymbol{b}-\boldsymbol{c}$
B.$\boldsymbol{a}-\boldsymbol{b}+\boldsymbol{c}$
C.$\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{c}$
D.$\boldsymbol{b}-\boldsymbol{a}-\boldsymbol{c}$
C
)
A.$\boldsymbol{a}+\boldsymbol{b}-\boldsymbol{c}$
B.$\boldsymbol{a}-\boldsymbol{b}+\boldsymbol{c}$
C.$\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{c}$
D.$\boldsymbol{b}-\boldsymbol{a}-\boldsymbol{c}$
答案:
4.C 【解析】依题意得,$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CD}-\overrightarrow{AB}$,即$\overrightarrow{BD}=\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{c}$.故选C.
5. [湖北武汉华中师大 一附中 2025 高一期中]化简以下各式,结果不是零向量的为(
A.$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}$
B.$\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BD}+\overrightarrow{CD}$
C.$\overrightarrow{OA}-\overrightarrow{OD}+\overrightarrow{AD}$
D.$\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MN}-\overrightarrow{MP}$
B
)A.$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}$
B.$\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BD}+\overrightarrow{CD}$
C.$\overrightarrow{OA}-\overrightarrow{OD}+\overrightarrow{AD}$
D.$\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MN}-\overrightarrow{MP}$
答案:
5.B 【解析】对于A:$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=0$,故A正确;
对于B:$\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BD}+\overrightarrow{CD}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{DB}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB}+\overrightarrow{AB}=\overrightarrow{AB}+\overrightarrow{AB}=2\overrightarrow{AB}$,故B错误;
对于C:$\overrightarrow{OA}-\overrightarrow{OD}+\overrightarrow{AD}=\overrightarrow{DA}+\overrightarrow{AD}=0$,故C正确;
对于D:$\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MN}-\overrightarrow{MP}=\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MN}+\overrightarrow{PM}=\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{PM}+\overrightarrow{MN}=0$,故D正确.
故选B.
对于B:$\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BD}+\overrightarrow{CD}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{DB}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB}+\overrightarrow{AB}=\overrightarrow{AB}+\overrightarrow{AB}=2\overrightarrow{AB}$,故B错误;
对于C:$\overrightarrow{OA}-\overrightarrow{OD}+\overrightarrow{AD}=\overrightarrow{DA}+\overrightarrow{AD}=0$,故C正确;
对于D:$\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MN}-\overrightarrow{MP}=\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MN}+\overrightarrow{PM}=\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{PM}+\overrightarrow{MN}=0$,故D正确.
故选B.
6. [广西柳州高中 2025 高一联考]在四边形$ABCD$中,$O$为任意一点,若$\overrightarrow{OA}-\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OD}=\boldsymbol{0}$,则四边形$ABCD$一定为(
A.矩形
B.菱形
C.等腰梯形
D.平行四边形
D
)A.矩形
B.菱形
C.等腰梯形
D.平行四边形
答案:
6.D 【解析】因为$\overrightarrow{OA}-\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OD}=0$,所以$\overrightarrow{BA}+\overrightarrow{DC}=0$,即$\overrightarrow{AB}=\overrightarrow{DC}$,
可知AB,CD两边平行且相等,所以四边形ABCD是平行四边形。
但没有足够条件判断四边形ABCD是否为矩形或菱形。故选D.
可知AB,CD两边平行且相等,所以四边形ABCD是平行四边形。
但没有足够条件判断四边形ABCD是否为矩形或菱形。故选D.
7. 已知$\overrightarrow{OA}=\boldsymbol{a}$,$\overrightarrow{OB}=\boldsymbol{b}$,$\overrightarrow{OC}=\boldsymbol{c}$,$\overrightarrow{OD}=\boldsymbol{d}$,$\overrightarrow{OE}=\boldsymbol{e}$,$\overrightarrow{OF}=\boldsymbol{f}$,试用$\boldsymbol{a}$,$\boldsymbol{b}$,$\boldsymbol{c}$,$\boldsymbol{d}$,$\boldsymbol{e}$,$\boldsymbol{f}$表示下列各式:
(1)$\overrightarrow{AD}-\overrightarrow{AB}$;(2)$\overrightarrow{AB}+\overrightarrow{CF}$;(3)$\overrightarrow{EF}-\overrightarrow{CF}$。
(1)$\overrightarrow{AD}-\overrightarrow{AB}$;(2)$\overrightarrow{AB}+\overrightarrow{CF}$;(3)$\overrightarrow{EF}-\overrightarrow{CF}$。
答案:
7.【解】
(1)$\overrightarrow{AD}-\overrightarrow{AB}=(\overrightarrow{OD}-\overrightarrow{OA})-(\overrightarrow{OB}-\overrightarrow{OA})=\overrightarrow{BD}=\overrightarrow{BO}+\overrightarrow{OD}=\overrightarrow{OD}-\overrightarrow{OB}$化简得$\boldsymbol{d}-\boldsymbol{a}-\boldsymbol{b}+\boldsymbol{a}=\boldsymbol{d}-\boldsymbol{b}$.
巧思:也可根据$\overrightarrow{AD}-\overrightarrow{AB}=\overrightarrow{BD}=\overrightarrow{BO}+\overrightarrow{OD}=\overrightarrow{OD}-\overrightarrow{OB}$化简
(2)$\overrightarrow{AB}+\overrightarrow{CF}=(\overrightarrow{OB}-\overrightarrow{OA})+(\overrightarrow{OF}-\overrightarrow{OC})=\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{f}-\boldsymbol{c}$.
(3)$\overrightarrow{EF}-\overrightarrow{CF}=(\overrightarrow{OF}-\overrightarrow{OE})-(\overrightarrow{OF}-\overrightarrow{OC})=\boldsymbol{f}-\boldsymbol{e}-\boldsymbol{f}+\boldsymbol{c}=\boldsymbol{c}-\boldsymbol{e}$.
(1)$\overrightarrow{AD}-\overrightarrow{AB}=(\overrightarrow{OD}-\overrightarrow{OA})-(\overrightarrow{OB}-\overrightarrow{OA})=\overrightarrow{BD}=\overrightarrow{BO}+\overrightarrow{OD}=\overrightarrow{OD}-\overrightarrow{OB}$化简得$\boldsymbol{d}-\boldsymbol{a}-\boldsymbol{b}+\boldsymbol{a}=\boldsymbol{d}-\boldsymbol{b}$.
巧思:也可根据$\overrightarrow{AD}-\overrightarrow{AB}=\overrightarrow{BD}=\overrightarrow{BO}+\overrightarrow{OD}=\overrightarrow{OD}-\overrightarrow{OB}$化简
(2)$\overrightarrow{AB}+\overrightarrow{CF}=(\overrightarrow{OB}-\overrightarrow{OA})+(\overrightarrow{OF}-\overrightarrow{OC})=\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{f}-\boldsymbol{c}$.
(3)$\overrightarrow{EF}-\overrightarrow{CF}=(\overrightarrow{OF}-\overrightarrow{OE})-(\overrightarrow{OF}-\overrightarrow{OC})=\boldsymbol{f}-\boldsymbol{e}-\boldsymbol{f}+\boldsymbol{c}=\boldsymbol{c}-\boldsymbol{e}$.
8. 在$\triangle ABC$中,若$|\overrightarrow{AB}|=|\overrightarrow{AC}|=|\overrightarrow{AB}-\overrightarrow{AC}|$,则$\triangle ABC$的形状为(
A.等边三角形
B.等腰(非等边)三角形
C.直角三角形
D.等腰直角三角形
A
)A.等边三角形
B.等腰(非等边)三角形
C.直角三角形
D.等腰直角三角形
答案:
8.A 【解析】因为$|\overrightarrow{AB}-\overrightarrow{AC}|=|\overrightarrow{CB}|,|\overrightarrow{AB}|=|\overrightarrow{AC}|=|\overrightarrow{AB}-\overrightarrow{AC}|$,所以$|\overrightarrow{AB}|=|\overrightarrow{AC}|=|\overrightarrow{CB}|$,所以$\triangle ABC$为等边三角形。故选A.
9. [陕西咸阳实验中学 2024 高一月考]设$\boldsymbol{a}$表示“向东走$6\mathrm{k}\mathrm{m}$”,$\boldsymbol{b}$表示“向南走$3\mathrm{k}\mathrm{m}$”,则$\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{b}$所表示的意义为(
A.向东南走$6\sqrt{2}\mathrm{k}\mathrm{m}$
B.向东南走$3\sqrt{6}\mathrm{k}\mathrm{m}$
C.向西南走$6\sqrt{2}\mathrm{k}\mathrm{m}$
D.向西南走$3\sqrt{6}\mathrm{k}\mathrm{m}$
C
)A.向东南走$6\sqrt{2}\mathrm{k}\mathrm{m}$
B.向东南走$3\sqrt{6}\mathrm{k}\mathrm{m}$
C.向西南走$6\sqrt{2}\mathrm{k}\mathrm{m}$
D.向西南走$3\sqrt{6}\mathrm{k}\mathrm{m}$
答案:
9.C 【解析】如图,分别作出$\overrightarrow{OA}=\boldsymbol{a},\overrightarrow{OC}=\boldsymbol{b},\overrightarrow{CB}=\boldsymbol{b}$,则利用向量加法的交换律可得$\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{b}+\boldsymbol{b}-\boldsymbol{a}$,故$\overrightarrow{AB}=\boldsymbol{b}+\boldsymbol{b}-\boldsymbol{a}$.
悟:$\boldsymbol{b}+\boldsymbol{b}=\overrightarrow{OC}+\overrightarrow{CB}=\overrightarrow{OB}$,$\boldsymbol{a}=\overrightarrow{OA}$,$-\boldsymbol{a}=\overrightarrow{AO}$,$\boldsymbol{b}+\boldsymbol{b}-\boldsymbol{a}=\overrightarrow{OB}+\overrightarrow{AO}=\overrightarrow{AB}$
易知$\triangle OAB$为等腰直角三角形,故$\angle OAB=45°$,且$|\overrightarrow{AB}|=6\sqrt{2}$,
于是$\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{b}$所表示的意义为向西南走$6\sqrt{2}km$.故选C.
9.C 【解析】如图,分别作出$\overrightarrow{OA}=\boldsymbol{a},\overrightarrow{OC}=\boldsymbol{b},\overrightarrow{CB}=\boldsymbol{b}$,则利用向量加法的交换律可得$\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{b}+\boldsymbol{b}-\boldsymbol{a}$,故$\overrightarrow{AB}=\boldsymbol{b}+\boldsymbol{b}-\boldsymbol{a}$.
悟:$\boldsymbol{b}+\boldsymbol{b}=\overrightarrow{OC}+\overrightarrow{CB}=\overrightarrow{OB}$,$\boldsymbol{a}=\overrightarrow{OA}$,$-\boldsymbol{a}=\overrightarrow{AO}$,$\boldsymbol{b}+\boldsymbol{b}-\boldsymbol{a}=\overrightarrow{OB}+\overrightarrow{AO}=\overrightarrow{AB}$

易知$\triangle OAB$为等腰直角三角形,故$\angle OAB=45°$,且$|\overrightarrow{AB}|=6\sqrt{2}$,
于是$\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{b}$所表示的意义为向西南走$6\sqrt{2}km$.故选C.
10. 已知$|\overrightarrow{AB}|=6$,$|\overrightarrow{AC}|=3$,则$|\overrightarrow{BC}|$的取值范围是(
A.$[3,6]$
B.$(3,6)$
C.$[3,9]$
D.$(3,9)$
C
)A.$[3,6]$
B.$(3,6)$
C.$[3,9]$
D.$(3,9)$
答案:
10.C 【解析】由题意得$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,所以$|\overrightarrow{BC}|=|\overrightarrow{AC}-\overrightarrow{AB}|$,所以$||\overrightarrow{AC}|-|\overrightarrow{AB}||\leq|\overrightarrow{BC}|\leq|\overrightarrow{AC}|+|\overrightarrow{AB}|$,则$3\leq|\overrightarrow{BC}|\leq9$,故C正确。故选C.
规律方法 向量和与差的三角不等式:$||\boldsymbol{a}|-|\boldsymbol{b}||\leq|\boldsymbol{a}\pm\boldsymbol{b}|\leq|\boldsymbol{a}|+|\boldsymbol{b}|$.

如图,可以借助三角形两边之差的绝对值小于第三边,两边之和大于第三边来记忆,取等号是共线的特殊情况。
10.C 【解析】由题意得$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,所以$|\overrightarrow{BC}|=|\overrightarrow{AC}-\overrightarrow{AB}|$,所以$||\overrightarrow{AC}|-|\overrightarrow{AB}||\leq|\overrightarrow{BC}|\leq|\overrightarrow{AC}|+|\overrightarrow{AB}|$,则$3\leq|\overrightarrow{BC}|\leq9$,故C正确。故选C.
规律方法 向量和与差的三角不等式:$||\boldsymbol{a}|-|\boldsymbol{b}||\leq|\boldsymbol{a}\pm\boldsymbol{b}|\leq|\boldsymbol{a}|+|\boldsymbol{b}|$.

如图,可以借助三角形两边之差的绝对值小于第三边,两边之和大于第三边来记忆,取等号是共线的特殊情况。
11. [北京二中 2025 高一月考]若$\boldsymbol{a}$,$\boldsymbol{b}$是非零向量,则“$|\boldsymbol{a}|=|\boldsymbol{b}|$”是“$|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|$”的(
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
D
)A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:
11.D 【解析】如图作$□ ABCD$,设$\overrightarrow{AB}=\boldsymbol{a}$,$\overrightarrow{AD}=\boldsymbol{b}$,

由向量加法的平行四边形法则知:由$|\boldsymbol{a}|=|\boldsymbol{b}|$可得$□ ABCD$是菱形,
因为菱形的对角线不一定相等,所以$|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|$不一定成立,即充分性不成立;
又由$|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|$可得$□ ABCD$是矩形,因为矩形的一组邻边不一定相等,所以$|\boldsymbol{a}|=|\boldsymbol{b}|$也不一定成立,即必要性不成立。
故“$|\boldsymbol{a}|=|\boldsymbol{b}|$”是“$|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|$”的既不充分也不必要条件。
故选D.
11.D 【解析】如图作$□ ABCD$,设$\overrightarrow{AB}=\boldsymbol{a}$,$\overrightarrow{AD}=\boldsymbol{b}$,

由向量加法的平行四边形法则知:由$|\boldsymbol{a}|=|\boldsymbol{b}|$可得$□ ABCD$是菱形,
因为菱形的对角线不一定相等,所以$|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|$不一定成立,即充分性不成立;
又由$|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|$可得$□ ABCD$是矩形,因为矩形的一组邻边不一定相等,所以$|\boldsymbol{a}|=|\boldsymbol{b}|$也不一定成立,即必要性不成立。
故“$|\boldsymbol{a}|=|\boldsymbol{b}|$”是“$|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|$”的既不充分也不必要条件。
故选D.
查看更多完整答案,请扫码查看


