2026年高中必刷题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年高中必刷题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [全国新高考Ⅰ2022·3,5 分]在△ABC 中,点 D 在边 AB 上,BD = 2DA。记$\overrightarrow{CA} = \boldsymbol{m}$,$\overrightarrow{CD} = \boldsymbol{n}$,则$\overrightarrow{CB}$ = (
A.$3\boldsymbol{m} - 2\boldsymbol{n}$
B.$-2\boldsymbol{m} + 3\boldsymbol{n}$
C.$3\boldsymbol{m} + 2\boldsymbol{n}$
D.$2\boldsymbol{m} + 3\boldsymbol{n}$
B
)A.$3\boldsymbol{m} - 2\boldsymbol{n}$
B.$-2\boldsymbol{m} + 3\boldsymbol{n}$
C.$3\boldsymbol{m} + 2\boldsymbol{n}$
D.$2\boldsymbol{m} + 3\boldsymbol{n}$
答案:
1.B [解析]如图,因为点D在边AB上,BD=2DA,所以$\overrightarrow{CB}=\overrightarrow{CA}+\overrightarrow{AB}=\overrightarrow{CA}+3\overrightarrow{AD}=\overrightarrow{CA}+3(\overrightarrow{CD}-\overrightarrow{CA})=-2\overrightarrow{CA}+3\overrightarrow{CD}=-2\boldsymbol{m}+3\boldsymbol{n}$,故选B.

1.B [解析]如图,因为点D在边AB上,BD=2DA,所以$\overrightarrow{CB}=\overrightarrow{CA}+\overrightarrow{AB}=\overrightarrow{CA}+3\overrightarrow{AD}=\overrightarrow{CA}+3(\overrightarrow{CD}-\overrightarrow{CA})=-2\overrightarrow{CA}+3\overrightarrow{CD}=-2\boldsymbol{m}+3\boldsymbol{n}$,故选B.

2. [全国新课标Ⅱ2024·3,5 分]已知向量$\boldsymbol{a}$,$\boldsymbol{b}$满足$\vert\boldsymbol{a}\vert = 1$,$\vert\boldsymbol{a} + 2\boldsymbol{b}\vert = 2$,且$(\boldsymbol{b} - 2\boldsymbol{a}) \perp \boldsymbol{b}$,则$\vert\boldsymbol{b}\vert$ = (
A.$\frac{1}{2}$
B.$\frac{\sqrt{2}}{2}$
C.$\frac{\sqrt{3}}{2}$
D.1
B
)A.$\frac{1}{2}$
B.$\frac{\sqrt{2}}{2}$
C.$\frac{\sqrt{3}}{2}$
D.1
答案:
2.B [解析]因为$(\boldsymbol{b}-2\boldsymbol{a})\perp\boldsymbol{b}$,所以$\boldsymbol{b}·\boldsymbol{b}-2\boldsymbol{a}·\boldsymbol{b}=0$,即$|\boldsymbol{b}|^{2}=2\boldsymbol{a}·\boldsymbol{b}$。又$|\boldsymbol{a}+2\boldsymbol{b}|=2$,所以$|\boldsymbol{a}+2\boldsymbol{b}|^{2}=(\boldsymbol{a}+2\boldsymbol{b})^{2}=\boldsymbol{a}^{2}+4\boldsymbol{a}·\boldsymbol{b}+4\boldsymbol{b}^{2}=\boldsymbol{a}^{2}+2\boldsymbol{b}^{2}+4\boldsymbol{b}^{2}=1 + 6|\boldsymbol{b}|^{2}=4$,解得$|\boldsymbol{b}|^{2}=\frac{1}{2}$,$|\boldsymbol{b}|=\frac{\sqrt{2}}{2}$,故选B。
3. [全国甲理 2023·4,5 分]已知向量$\boldsymbol{a}$,$\boldsymbol{b}$,$\boldsymbol{c}$满足$\vert\boldsymbol{a}\vert = \vert\boldsymbol{b}\vert = 1$,$\vert\boldsymbol{c}\vert = \sqrt{2}$,且$\boldsymbol{a} + \boldsymbol{b} + \boldsymbol{c} = \boldsymbol{0}$,则$\cos\langle\boldsymbol{a} - \boldsymbol{c}, \boldsymbol{b} - \boldsymbol{c}\rangle$ = (
A.$-\frac{4}{5}$
B.$-\frac{2}{5}$
C.$\frac{2}{5}$
D.$\frac{4}{5}$
D
)A.$-\frac{4}{5}$
B.$-\frac{2}{5}$
C.$\frac{2}{5}$
D.$\frac{4}{5}$
答案:
3.D [解析]设$\overrightarrow{OA}=\boldsymbol{a}$,$\overrightarrow{OB}=\boldsymbol{b}$,$\overrightarrow{OC}=\boldsymbol{c}$,因为$|\boldsymbol{a}|=|\boldsymbol{b}| = 1$,$|\boldsymbol{c}|=\sqrt{2}$,且$\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}=0$,所以$\boldsymbol{a}\perp\boldsymbol{b}$,如图。

因为$\boldsymbol{a}-\boldsymbol{c}=\overrightarrow{OA}-\overrightarrow{OC}=\overrightarrow{CA}$,$\boldsymbol{b}-\boldsymbol{c}=\overrightarrow{OB}-\overrightarrow{OC}=\overrightarrow{CB}$,所以$\langle\boldsymbol{a}-\boldsymbol{c},\boldsymbol{b}-\boldsymbol{c}\rangle=\angle ACB$。
由题意可知,$\angle AOC=\angle BOC=\frac{3\pi}{4}$,在$\triangle AOC$中,由余弦定理得,$AC^{2}=OA^{2}+OC^{2}-2OA· OC·\cos\angle AOC=1^{2}+(\sqrt{2})^{2}-2×1×\sqrt{2}×(-\frac{\sqrt{2}}{2}) = 5$,所以$AC = BC=\sqrt{5}$。在$\triangle ABC$中,$AB = \sqrt{2}$,由余弦定理得,$\cos\angle ACB=\frac{AC^{2}+BC^{2}-AB^{2}}{2AC· BC}=\frac{(\sqrt{5})^{2}+(\sqrt{5})^{2}-(\sqrt{2})^{2}}{2\sqrt{5}×\sqrt{5}}=\frac{4}{5}$,所以$\cos\langle\boldsymbol{a}-\boldsymbol{c},\boldsymbol{b}-\boldsymbol{c}\rangle=\frac{4}{5}$,故选D。
多种解法:由$\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}=0$得,$\boldsymbol{a}+\boldsymbol{b}=-\boldsymbol{c}$,则$(\boldsymbol{a}+\boldsymbol{b})^{2}=\boldsymbol{c}^{2}\Leftrightarrow\boldsymbol{a}^{2}+2\boldsymbol{a}·\boldsymbol{b}+\boldsymbol{b}^{2}=\boldsymbol{c}^{2}$,即$1^{2}+2\boldsymbol{a}·\boldsymbol{b}+1^{2}=(\sqrt{2})^{2}$,解得$\boldsymbol{a}·\boldsymbol{b}=0$。又$\boldsymbol{a}+\boldsymbol{c}=-\boldsymbol{b}$,则$(\boldsymbol{a}+\boldsymbol{c})^{2}=\boldsymbol{b}^{2}\Leftrightarrow\boldsymbol{a}^{2}+2\boldsymbol{a}·\boldsymbol{c}+\boldsymbol{c}^{2}=\boldsymbol{b}^{2}$,即$1^{2}+2\boldsymbol{a}·\boldsymbol{c}+(\sqrt{2})^{2}=1^{2}$,解得$\boldsymbol{a}·\boldsymbol{c}=-1$,同理可得$\boldsymbol{b}·\boldsymbol{c}=-1$,所以$(\boldsymbol{a}-\boldsymbol{c})·(\boldsymbol{b}-\boldsymbol{c})=\boldsymbol{a}·\boldsymbol{b}-\boldsymbol{a}·\boldsymbol{c}-\boldsymbol{b}·\boldsymbol{c}+\boldsymbol{c}^{2}=0 - (-1) - (-1)+(\sqrt{2})^{2}=4$,$|\boldsymbol{a}-\boldsymbol{c}|=\sqrt{\boldsymbol{a}^{2}-2\boldsymbol{a}·\boldsymbol{c}+\boldsymbol{c}^{2}}=\sqrt{5}$,$|\boldsymbol{b}-\boldsymbol{c}|=\sqrt{\boldsymbol{b}^{2}-2\boldsymbol{b}·\boldsymbol{c}+\boldsymbol{c}^{2}}=\sqrt{5}$,所以$\cos\langle\boldsymbol{a}-\boldsymbol{c},\boldsymbol{b}-\boldsymbol{c}\rangle=\frac{(\boldsymbol{a}-\boldsymbol{c})·(\boldsymbol{b}-\boldsymbol{c})}{|\boldsymbol{a}-\boldsymbol{c}||\boldsymbol{b}-\boldsymbol{c}|}=\frac{4}{\sqrt{5}×\sqrt{5}}=\frac{4}{5}$,故选D。
3.D [解析]设$\overrightarrow{OA}=\boldsymbol{a}$,$\overrightarrow{OB}=\boldsymbol{b}$,$\overrightarrow{OC}=\boldsymbol{c}$,因为$|\boldsymbol{a}|=|\boldsymbol{b}| = 1$,$|\boldsymbol{c}|=\sqrt{2}$,且$\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}=0$,所以$\boldsymbol{a}\perp\boldsymbol{b}$,如图。

因为$\boldsymbol{a}-\boldsymbol{c}=\overrightarrow{OA}-\overrightarrow{OC}=\overrightarrow{CA}$,$\boldsymbol{b}-\boldsymbol{c}=\overrightarrow{OB}-\overrightarrow{OC}=\overrightarrow{CB}$,所以$\langle\boldsymbol{a}-\boldsymbol{c},\boldsymbol{b}-\boldsymbol{c}\rangle=\angle ACB$。
由题意可知,$\angle AOC=\angle BOC=\frac{3\pi}{4}$,在$\triangle AOC$中,由余弦定理得,$AC^{2}=OA^{2}+OC^{2}-2OA· OC·\cos\angle AOC=1^{2}+(\sqrt{2})^{2}-2×1×\sqrt{2}×(-\frac{\sqrt{2}}{2}) = 5$,所以$AC = BC=\sqrt{5}$。在$\triangle ABC$中,$AB = \sqrt{2}$,由余弦定理得,$\cos\angle ACB=\frac{AC^{2}+BC^{2}-AB^{2}}{2AC· BC}=\frac{(\sqrt{5})^{2}+(\sqrt{5})^{2}-(\sqrt{2})^{2}}{2\sqrt{5}×\sqrt{5}}=\frac{4}{5}$,所以$\cos\langle\boldsymbol{a}-\boldsymbol{c},\boldsymbol{b}-\boldsymbol{c}\rangle=\frac{4}{5}$,故选D。
多种解法:由$\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}=0$得,$\boldsymbol{a}+\boldsymbol{b}=-\boldsymbol{c}$,则$(\boldsymbol{a}+\boldsymbol{b})^{2}=\boldsymbol{c}^{2}\Leftrightarrow\boldsymbol{a}^{2}+2\boldsymbol{a}·\boldsymbol{b}+\boldsymbol{b}^{2}=\boldsymbol{c}^{2}$,即$1^{2}+2\boldsymbol{a}·\boldsymbol{b}+1^{2}=(\sqrt{2})^{2}$,解得$\boldsymbol{a}·\boldsymbol{b}=0$。又$\boldsymbol{a}+\boldsymbol{c}=-\boldsymbol{b}$,则$(\boldsymbol{a}+\boldsymbol{c})^{2}=\boldsymbol{b}^{2}\Leftrightarrow\boldsymbol{a}^{2}+2\boldsymbol{a}·\boldsymbol{c}+\boldsymbol{c}^{2}=\boldsymbol{b}^{2}$,即$1^{2}+2\boldsymbol{a}·\boldsymbol{c}+(\sqrt{2})^{2}=1^{2}$,解得$\boldsymbol{a}·\boldsymbol{c}=-1$,同理可得$\boldsymbol{b}·\boldsymbol{c}=-1$,所以$(\boldsymbol{a}-\boldsymbol{c})·(\boldsymbol{b}-\boldsymbol{c})=\boldsymbol{a}·\boldsymbol{b}-\boldsymbol{a}·\boldsymbol{c}-\boldsymbol{b}·\boldsymbol{c}+\boldsymbol{c}^{2}=0 - (-1) - (-1)+(\sqrt{2})^{2}=4$,$|\boldsymbol{a}-\boldsymbol{c}|=\sqrt{\boldsymbol{a}^{2}-2\boldsymbol{a}·\boldsymbol{c}+\boldsymbol{c}^{2}}=\sqrt{5}$,$|\boldsymbol{b}-\boldsymbol{c}|=\sqrt{\boldsymbol{b}^{2}-2\boldsymbol{b}·\boldsymbol{c}+\boldsymbol{c}^{2}}=\sqrt{5}$,所以$\cos\langle\boldsymbol{a}-\boldsymbol{c},\boldsymbol{b}-\boldsymbol{c}\rangle=\frac{(\boldsymbol{a}-\boldsymbol{c})·(\boldsymbol{b}-\boldsymbol{c})}{|\boldsymbol{a}-\boldsymbol{c}||\boldsymbol{b}-\boldsymbol{c}|}=\frac{4}{\sqrt{5}×\sqrt{5}}=\frac{4}{5}$,故选D。
4. 教材变式[全国一 2025·6,5 分]帆船比赛中,运动员可借助风力计测定风速的大小与方向,测出的结果在航海学中称为视风风速。视风风速对应的向量是真风风速对应的向量与船行风风速对应的向量之和,其中船行风风速对应的向量与船速对应的向量大小相等、方向相反。表中给出了部分风力等级、名称与风速大小的对应关系。已知某帆船运动员在某时刻测得的视风风速对应的向量与船速对应的向量如图所示(线段长度代表速度大小,单位:m/s),则该时刻的真风为 (

A.轻风
B.微风
C.和风
D.劲风
A
)
A.轻风
B.微风
C.和风
D.劲风
答案:
4.A [解析]如图,设点$A(3,3)$,$B(0,2)$,$C(2,0)$,由题意知,视风风速对应的向量为$\overrightarrow{AB}$,船速对应的向量为$\overrightarrow{CA}$,因为船行风风速对应的向量与船速对应的向量为相反向量,所以船行风风速对应的向量为$\overrightarrow{AC}$,则真风风速对应的向量为$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}=(-2,2)$,$|\overrightarrow{CB}|=\sqrt{(-2)^{2}+2^{2}}=2\sqrt{2}$,而$2\sqrt{2}\in(1.6,3.3)$,故该时刻的真风为轻风。故选A。
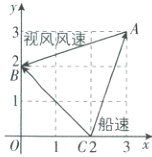
链接教材:此题是教材第9页例2的变式题,以船航行为背景考查向量的线性运算。
4.A [解析]如图,设点$A(3,3)$,$B(0,2)$,$C(2,0)$,由题意知,视风风速对应的向量为$\overrightarrow{AB}$,船速对应的向量为$\overrightarrow{CA}$,因为船行风风速对应的向量与船速对应的向量为相反向量,所以船行风风速对应的向量为$\overrightarrow{AC}$,则真风风速对应的向量为$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}=(-2,2)$,$|\overrightarrow{CB}|=\sqrt{(-2)^{2}+2^{2}}=2\sqrt{2}$,而$2\sqrt{2}\in(1.6,3.3)$,故该时刻的真风为轻风。故选A。

链接教材:此题是教材第9页例2的变式题,以船航行为背景考查向量的线性运算。
5. [北京 2025·10,4 分]在平面直角坐标系 xOy 中,$\vert\overrightarrow{OA}\vert = \vert\overrightarrow{OB}\vert = \sqrt{2}$,$\vert\overrightarrow{AB}\vert = 2$,设 C(3,4),则$\vert 2\overrightarrow{CA} + \overrightarrow{AB}\vert$的取值范围是 (
A.[6,14]
B.[6,12]
C.[8,14]
D.[8,12]
D
)A.[6,14]
B.[6,12]
C.[8,14]
D.[8,12]
答案:
5.D [解析]因为$|\overrightarrow{OA}|=|\overrightarrow{OB}|=\sqrt{2}$,$|\overrightarrow{AB}| = 2$,所以$|\overrightarrow{OA}|^{2}+|\overrightarrow{OB}|^{2}=|\overrightarrow{AB}|^{2}=4$,所以$OA\perp OB$且点$A$,$B$在以点$O$为圆心,$\sqrt{2}$为半径的圆上。所以$|2\overrightarrow{CA}+\overrightarrow{AB}|=|\overrightarrow{CA}+\overrightarrow{CB}|=|\overrightarrow{OA}-\overrightarrow{OC}+\overrightarrow{OB}-\overrightarrow{OC}|=|\overrightarrow{OA}+\overrightarrow{OB}-2\overrightarrow{OC}|$,所以$|2\overrightarrow{CA}+\overrightarrow{AB}|^{2}=(\overrightarrow{OA}+\overrightarrow{OB})^{2}+4\overrightarrow{OC}^{2}-4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}=\overrightarrow{OA}^{2}+\overrightarrow{OB}^{2}+4\overrightarrow{OC}^{2}-4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}=4 + 4\overrightarrow{OC}^{2}-4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}$。
令$\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OB}$,则点$D$在以点$O$为圆心,$2$为半径的圆上,所以$(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}=\overrightarrow{OD}·\overrightarrow{OC}=|\overrightarrow{OD}||\overrightarrow{OC}|\cos\langle\overrightarrow{OD},\overrightarrow{OC}\rangle = 2×2\cos\langle\overrightarrow{OD},\overrightarrow{OC}\rangle = 4\cos\langle\overrightarrow{OD},\overrightarrow{OC}\rangle$。
因为$\langle\overrightarrow{OD},\overrightarrow{OC}\rangle\in[0,\pi]$,所以$(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}\in[-4,4]$,所以$|2\overrightarrow{CA}+\overrightarrow{AB}|^{2}=4 + 4\overrightarrow{OC}^{2}-4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}\in[64,144]$,所以$|2\overrightarrow{CA}+\overrightarrow{AB}|\in[8,12]$。故选D。

5.D [解析]因为$|\overrightarrow{OA}|=|\overrightarrow{OB}|=\sqrt{2}$,$|\overrightarrow{AB}| = 2$,所以$|\overrightarrow{OA}|^{2}+|\overrightarrow{OB}|^{2}=|\overrightarrow{AB}|^{2}=4$,所以$OA\perp OB$且点$A$,$B$在以点$O$为圆心,$\sqrt{2}$为半径的圆上。所以$|2\overrightarrow{CA}+\overrightarrow{AB}|=|\overrightarrow{CA}+\overrightarrow{CB}|=|\overrightarrow{OA}-\overrightarrow{OC}+\overrightarrow{OB}-\overrightarrow{OC}|=|\overrightarrow{OA}+\overrightarrow{OB}-2\overrightarrow{OC}|$,所以$|2\overrightarrow{CA}+\overrightarrow{AB}|^{2}=(\overrightarrow{OA}+\overrightarrow{OB})^{2}+4\overrightarrow{OC}^{2}-4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}=\overrightarrow{OA}^{2}+\overrightarrow{OB}^{2}+4\overrightarrow{OC}^{2}-4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}=4 + 4\overrightarrow{OC}^{2}-4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}$。
令$\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OB}$,则点$D$在以点$O$为圆心,$2$为半径的圆上,所以$(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}=\overrightarrow{OD}·\overrightarrow{OC}=|\overrightarrow{OD}||\overrightarrow{OC}|\cos\langle\overrightarrow{OD},\overrightarrow{OC}\rangle = 2×2\cos\langle\overrightarrow{OD},\overrightarrow{OC}\rangle = 4\cos\langle\overrightarrow{OD},\overrightarrow{OC}\rangle$。
因为$\langle\overrightarrow{OD},\overrightarrow{OC}\rangle\in[0,\pi]$,所以$(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}\in[-4,4]$,所以$|2\overrightarrow{CA}+\overrightarrow{AB}|^{2}=4 + 4\overrightarrow{OC}^{2}-4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}\in[64,144]$,所以$|2\overrightarrow{CA}+\overrightarrow{AB}|\in[8,12]$。故选D。

6. [全国乙理 2023·12,5 分]已知⊙O 的半径为 1,直线 PA 与⊙O 相切于点 A,直线 PB 与⊙O 交于 B,C 两点,D 为 BC 的中点。若$\vert PO\vert = \sqrt{2}$,则$\overrightarrow{PA} · \overrightarrow{PD}$的最大值为 (
A.$\frac{1}{2} + \frac{\sqrt{2}}{2}$
B.$\frac{1}{2} + \sqrt{2}$
C.$1 + \sqrt{2}$
D.$2 + \sqrt{2}$
A
)A.$\frac{1}{2} + \frac{\sqrt{2}}{2}$
B.$\frac{1}{2} + \sqrt{2}$
C.$1 + \sqrt{2}$
D.$2 + \sqrt{2}$
答案:
6.A
思路导引:$|\overrightarrow{PO}|=\sqrt{2}$,$\odot O$的半径为$1\to|\overrightarrow{PA}|\to$设$\overrightarrow{PO}$与$\overrightarrow{PD}$的夹角为$\theta\to$分$\overrightarrow{PA}$与$\overrightarrow{PD}$在$\overrightarrow{PO}$同侧与异侧讨论$\overrightarrow{PA}·\overrightarrow{PD}$,比较得最值。
[解析]直线$PA$与$\odot O$相切于$A$,且$|\overrightarrow{OA}| = 1$,$|\overrightarrow{PO}|=\sqrt{2}$,则$|\overrightarrow{PA}| = 1$。设$\overrightarrow{PO}$与$\overrightarrow{PD}$的夹角为$\theta$,则$\theta\in[0,\frac{\pi}{4})$。
当$\overrightarrow{PA}$与$\overrightarrow{PD}$在$\overrightarrow{PO}$的同侧时,$\overrightarrow{PA}·\overrightarrow{PD}=|\overrightarrow{PA}||\overrightarrow{PD}|\cos(\frac{\pi}{4}-\theta)=1×|\overrightarrow{PO}|\cos\theta×\cos(\frac{\pi}{4}-\theta)=\sqrt{2}\cos\theta·\cos(\frac{\pi}{4}-\theta)=\sqrt{2}\cos\theta×\frac{\sqrt{2}}{2}(\cos\theta+\sin\theta)=\cos^{2}\theta+\frac{1}{2}\sin2\theta=\frac{1}{2}+\frac{\sqrt{2}}{2}\sin(2\theta+\frac{\pi}{4})\leq\frac{1}{2}+\frac{\sqrt{2}}{2}$;
当$\overrightarrow{PA}$与$\overrightarrow{PD}$在$\overrightarrow{PO}$的异侧时,$\overrightarrow{PA}·\overrightarrow{PD}=|\overrightarrow{PA}||\overrightarrow{PD}|\cos(\frac{\pi}{4}+\theta)=1×|\overrightarrow{PO}|\cos\theta×\cos(\frac{\pi}{4}+\theta)=\sqrt{2}\cos\theta·\cos(\frac{\pi}{4}+\theta)=\sqrt{2}\cos\theta×\frac{\sqrt{2}}{2}(\cos\theta-\sin\theta)=\cos^{2}\theta-\frac{1}{2}\sin2\theta=\frac{1}{2}+\frac{\sqrt{2}}{2}\cos(2\theta+\frac{\pi}{4})\leq\frac{1}{2}+\frac{\sqrt{2}}{2}$。
综上所述,$\overrightarrow{PA}·\overrightarrow{PD}$的最大值为$\frac{1}{2}+\frac{\sqrt{2}}{2}$,故选A。
多种解法:由题知点$D$为弦$BC$的中点,如图,所以$OD\perp BC$,点$D$在以$OP$为直径的圆上运动,且在圆$O$内,所以$\overrightarrow{PA}·\overrightarrow{PD}$的最大值为$\frac{1}{2}+\frac{\sqrt{2}}{2}$,故选A。

6.A
思路导引:$|\overrightarrow{PO}|=\sqrt{2}$,$\odot O$的半径为$1\to|\overrightarrow{PA}|\to$设$\overrightarrow{PO}$与$\overrightarrow{PD}$的夹角为$\theta\to$分$\overrightarrow{PA}$与$\overrightarrow{PD}$在$\overrightarrow{PO}$同侧与异侧讨论$\overrightarrow{PA}·\overrightarrow{PD}$,比较得最值。
[解析]直线$PA$与$\odot O$相切于$A$,且$|\overrightarrow{OA}| = 1$,$|\overrightarrow{PO}|=\sqrt{2}$,则$|\overrightarrow{PA}| = 1$。设$\overrightarrow{PO}$与$\overrightarrow{PD}$的夹角为$\theta$,则$\theta\in[0,\frac{\pi}{4})$。
当$\overrightarrow{PA}$与$\overrightarrow{PD}$在$\overrightarrow{PO}$的同侧时,$\overrightarrow{PA}·\overrightarrow{PD}=|\overrightarrow{PA}||\overrightarrow{PD}|\cos(\frac{\pi}{4}-\theta)=1×|\overrightarrow{PO}|\cos\theta×\cos(\frac{\pi}{4}-\theta)=\sqrt{2}\cos\theta·\cos(\frac{\pi}{4}-\theta)=\sqrt{2}\cos\theta×\frac{\sqrt{2}}{2}(\cos\theta+\sin\theta)=\cos^{2}\theta+\frac{1}{2}\sin2\theta=\frac{1}{2}+\frac{\sqrt{2}}{2}\sin(2\theta+\frac{\pi}{4})\leq\frac{1}{2}+\frac{\sqrt{2}}{2}$;
当$\overrightarrow{PA}$与$\overrightarrow{PD}$在$\overrightarrow{PO}$的异侧时,$\overrightarrow{PA}·\overrightarrow{PD}=|\overrightarrow{PA}||\overrightarrow{PD}|\cos(\frac{\pi}{4}+\theta)=1×|\overrightarrow{PO}|\cos\theta×\cos(\frac{\pi}{4}+\theta)=\sqrt{2}\cos\theta·\cos(\frac{\pi}{4}+\theta)=\sqrt{2}\cos\theta×\frac{\sqrt{2}}{2}(\cos\theta-\sin\theta)=\cos^{2}\theta-\frac{1}{2}\sin2\theta=\frac{1}{2}+\frac{\sqrt{2}}{2}\cos(2\theta+\frac{\pi}{4})\leq\frac{1}{2}+\frac{\sqrt{2}}{2}$。
综上所述,$\overrightarrow{PA}·\overrightarrow{PD}$的最大值为$\frac{1}{2}+\frac{\sqrt{2}}{2}$,故选A。
多种解法:由题知点$D$为弦$BC$的中点,如图,所以$OD\perp BC$,点$D$在以$OP$为直径的圆上运动,且在圆$O$内,所以$\overrightarrow{PA}·\overrightarrow{PD}$的最大值为$\frac{1}{2}+\frac{\sqrt{2}}{2}$,故选A。

7. (多选)[全国新高考Ⅰ2021·10,5 分]已知 O 为坐标原点,点$P_1(\cos\alpha, \sin\alpha)$,$P_2(\cos\beta, -\sin\beta)$,$P_3(\cos(\alpha + \beta), \sin(\alpha + \beta))$,A(1,0),则 (
A.$\vert\overrightarrow{OP_1}\vert = \vert\overrightarrow{OP_2}\vert$
B.$\vert\overrightarrow{AP_1}\vert = \vert\overrightarrow{AP_2}\vert$
C.$\overrightarrow{OA} · \overrightarrow{OP_3} = \overrightarrow{OP_1} · \overrightarrow{OP_2}$
D.$\overrightarrow{OA} · \overrightarrow{OP_1} = \overrightarrow{OP_2} · \overrightarrow{OP_3}$
AC
)A.$\vert\overrightarrow{OP_1}\vert = \vert\overrightarrow{OP_2}\vert$
B.$\vert\overrightarrow{AP_1}\vert = \vert\overrightarrow{AP_2}\vert$
C.$\overrightarrow{OA} · \overrightarrow{OP_3} = \overrightarrow{OP_1} · \overrightarrow{OP_2}$
D.$\overrightarrow{OA} · \overrightarrow{OP_1} = \overrightarrow{OP_2} · \overrightarrow{OP_3}$
答案:
7.AC [解析]对于选项A,因为$\overrightarrow{OP_{1}}=(\cos\alpha,\sin\alpha)$,$\overrightarrow{OP_{2}}=(\cos\beta,-\sin\beta)$,所以$|\overrightarrow{OP_{1}}|=\sqrt{\cos^{2}\alpha+\sin^{2}\alpha}=1$,$|\overrightarrow{OP_{2}}|=\sqrt{\cos^{2}\beta+(-\sin\beta)^{2}} = 1$,则$|\overrightarrow{OP_{1}}|=|\overrightarrow{OP_{2}}|$,故A正确;对于选项B,因为$\overrightarrow{AP_{1}}=(\cos\alpha - 1,\sin\alpha)$,$\overrightarrow{AP_{2}}=(\cos\beta - 1,-\sin\beta)$,所以$|\overrightarrow{AP_{1}}|=\sqrt{(\cos\alpha - 1)^{2}+\sin^{2}\alpha}=\sqrt{2 - 2\cos\alpha}$,$|\overrightarrow{AP_{2}}|=\sqrt{(\cos\beta - 1)^{2}+(-\sin\beta)^{2}}=\sqrt{2 - 2\cos\beta}$,当$\cos\alpha\neq\cos\beta$时,$|\overrightarrow{AP_{1}}|\neq|\overrightarrow{AP_{2}}|$,故B错误;对于选项C,$\overrightarrow{OA}=(1,0)$,$\overrightarrow{OP_{1}}=(\cos(\alpha + \beta),\sin(\alpha + \beta))$,所以$\overrightarrow{OA}·\overrightarrow{OP_{1}}=\cos(\alpha + \beta)$,$\overrightarrow{OP_{1}}·\overrightarrow{OP_{2}}=\cos\alpha\cos\beta-\sin\alpha\sin\beta=\cos(\alpha + \beta)$,所以$\overrightarrow{OA}·\overrightarrow{OP_{1}}=\overrightarrow{OP_{1}}·\overrightarrow{OP_{2}}$,故C正确;对于选项D,$\overrightarrow{OA}·\overrightarrow{OP_{1}}=\cos\alpha$,$\overrightarrow{OP_{1}}·\overrightarrow{OP_{2}}=\cos\beta\cos(\alpha + \beta)-\sin\beta\sin(\alpha + \beta)=\cos(\alpha + 2\beta)$,当$\beta\neq k\pi$且$\beta\neq k\pi - \alpha(k\in Z)$时,$\overrightarrow{OA}·\overrightarrow{OP_{1}}\neq\overrightarrow{OP_{1}}·\overrightarrow{OP_{2}}$,故D错误。故选AC。
8. [天津 2025·14,5 分]在△ABC 中,D 为 AB 中点,$\overrightarrow{CE} = \frac{1}{3}\overrightarrow{CD}$,记$\overrightarrow{AB} = \boldsymbol{a}$,$\overrightarrow{AC} = \boldsymbol{b}$,则$\overrightarrow{AE}$ =
$\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}$
(用$\boldsymbol{a}$,$\boldsymbol{b}$表示);若$\vert\overrightarrow{AE}\vert = 5$,$AE \perp CB$,则$\overrightarrow{AE} · \overrightarrow{CD}$ = -15
。
答案:
8.$\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}$ $-15$ [解析]依题意,$\overrightarrow{AE}=\overrightarrow{AC}+\overrightarrow{CE}=\boldsymbol{b}+\frac{1}{3}\overrightarrow{CD}$,因为$D$是$AB$中点,所以$\overrightarrow{CD}=\frac{1}{2}\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CB}=\frac{1}{2}\overrightarrow{CA}+\frac{1}{2}(\overrightarrow{AB}-\overrightarrow{AC})=\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC}=\frac{1}{2}\boldsymbol{a}-\boldsymbol{b}$,所以$\overrightarrow{AE}=\boldsymbol{b}+\frac{1}{3}(\frac{1}{2}\boldsymbol{a}-\boldsymbol{b})=\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}$。
因为$|\overrightarrow{AE}| = 5$,$\overrightarrow{AE}\perp\overrightarrow{CB}$,所以$\begin{cases}(\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b})^{2}=25\\(\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b})·(\boldsymbol{a}-\boldsymbol{b})=0\end{cases}$,即$\begin{cases}\frac{1}{36}|\boldsymbol{a}|^{2}+\frac{2}{9}\boldsymbol{a}·\boldsymbol{b}+\frac{4}{9}|\boldsymbol{b}|^{2}=25\frac{1}{6}|\boldsymbol{a}|^{2}+\frac{1}{2}\boldsymbol{a}·\boldsymbol{b}-\frac{2}{3}|\boldsymbol{b}|^{2}=0\end{cases}$,即$\begin{cases}|\boldsymbol{a}|^{2}+8\boldsymbol{a}·\boldsymbol{b}+16|\boldsymbol{b}|^{2}=900\\|\boldsymbol{a}|^{2}-4|\boldsymbol{b}|^{2}+3\boldsymbol{a}·\boldsymbol{b}=0\end{cases}$。
由②得$|\boldsymbol{a}|^{2}=4|\boldsymbol{b}|^{2}-3\boldsymbol{a}·\boldsymbol{b}$,代入①得$20|\boldsymbol{b}|^{2}+5\boldsymbol{a}·\boldsymbol{b}=900$。
则$\overrightarrow{AE}·\overrightarrow{CD}=(\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b})·(\frac{1}{2}\boldsymbol{a}-\boldsymbol{b})=\frac{1}{12}|\boldsymbol{a}|^{2}+\frac{1}{6}\boldsymbol{a}·\boldsymbol{b}-\frac{2}{3}|\boldsymbol{b}|^{2}=-\frac{1}{3}|\boldsymbol{b}|^{2}-\frac{1}{12}\boldsymbol{a}·\boldsymbol{b}=-\frac{1}{60}(20|\boldsymbol{b}|^{2}+5\boldsymbol{a}·\boldsymbol{b})=-15$。
多种解法一:如图,延长$AE$交$BC$于$F$,则$AF\perp BC$,过$D$作$DG\perp AF$于$G$,所以$\triangle CEF\sim\triangle DEG$。

设$EF = x$,则$\frac{EG}{EF}=\frac{DE}{EC}=\frac{2}{1}$,所以$EG = 2x$。又$D$为$AB$中点,$DG// BF$,所以$AG = FG = 3x$,所以$AE = AG + GE = 3x + 2x = 5$,解得$x = 1$,即$EF = 1$。
所以$\overrightarrow{AE}·\overrightarrow{CD}=\overrightarrow{AE}·3\overrightarrow{CE}=3|\overrightarrow{AE}||\overrightarrow{CE}|\cos\langle\overrightarrow{AE},\overrightarrow{CE}\rangle=3|\overrightarrow{AE}||\overrightarrow{CE}|(-\cos\angle CEF)=-3|\overrightarrow{AE}|·|\overrightarrow{EF}|=-15$。
多种解法二:延长$AE$交$BC$于$F$,则$AF\perp BC$。
$\overrightarrow{AE}·\overrightarrow{CD}=\overrightarrow{AE}·(\overrightarrow{CB}+\overrightarrow{BD})=\overrightarrow{AE}·\overrightarrow{CB}+\overrightarrow{AE}·\overrightarrow{BD}=0+\overrightarrow{AE}·(-\frac{1}{2}\overrightarrow{AB})=-\frac{1}{2}\overrightarrow{AE}·\overrightarrow{AB}$。
设$\overrightarrow{AE}$与$\overrightarrow{AB}$的夹角为$\theta$,则$\overrightarrow{AE}·\overrightarrow{CD}=-\frac{1}{2}·|\overrightarrow{AE}|·|\overrightarrow{AB}|\cos\theta=-\frac{1}{2}×5×|\overrightarrow{AF}|$。
设$\overrightarrow{AF}=\lambda\overrightarrow{AE}=\lambda(\frac{2}{3}\overrightarrow{AC}+\frac{1}{6}\overrightarrow{AB})=\frac{2}{3}\lambda\overrightarrow{AC}+\frac{\lambda}{6}\overrightarrow{AB}$,因为$B$,$F$,$C$三点共线,所以$\frac{2}{3}\lambda+\frac{\lambda}{6}=1$,解得$\lambda=\frac{6}{5}$。
所以$\overrightarrow{AF}=\frac{6}{5}\overrightarrow{AE}$,即$|\overrightarrow{AF}| = 6$,所以$\overrightarrow{AE}·\overrightarrow{CD}=-\frac{1}{2}×5×6=-15$。
二级结论:在$\triangle ABC$中,$D$为线段$BC$上一点,若$\frac{BD}{DC}=\frac{m}{n}$,则$\overrightarrow{AD}=\frac{m}{m + n}·\overrightarrow{AC}+\frac{n}{m + n}\overrightarrow{AB}$。
8.$\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}$ $-15$ [解析]依题意,$\overrightarrow{AE}=\overrightarrow{AC}+\overrightarrow{CE}=\boldsymbol{b}+\frac{1}{3}\overrightarrow{CD}$,因为$D$是$AB$中点,所以$\overrightarrow{CD}=\frac{1}{2}\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CB}=\frac{1}{2}\overrightarrow{CA}+\frac{1}{2}(\overrightarrow{AB}-\overrightarrow{AC})=\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC}=\frac{1}{2}\boldsymbol{a}-\boldsymbol{b}$,所以$\overrightarrow{AE}=\boldsymbol{b}+\frac{1}{3}(\frac{1}{2}\boldsymbol{a}-\boldsymbol{b})=\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}$。
因为$|\overrightarrow{AE}| = 5$,$\overrightarrow{AE}\perp\overrightarrow{CB}$,所以$\begin{cases}(\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b})^{2}=25\\(\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b})·(\boldsymbol{a}-\boldsymbol{b})=0\end{cases}$,即$\begin{cases}\frac{1}{36}|\boldsymbol{a}|^{2}+\frac{2}{9}\boldsymbol{a}·\boldsymbol{b}+\frac{4}{9}|\boldsymbol{b}|^{2}=25\frac{1}{6}|\boldsymbol{a}|^{2}+\frac{1}{2}\boldsymbol{a}·\boldsymbol{b}-\frac{2}{3}|\boldsymbol{b}|^{2}=0\end{cases}$,即$\begin{cases}|\boldsymbol{a}|^{2}+8\boldsymbol{a}·\boldsymbol{b}+16|\boldsymbol{b}|^{2}=900\\|\boldsymbol{a}|^{2}-4|\boldsymbol{b}|^{2}+3\boldsymbol{a}·\boldsymbol{b}=0\end{cases}$。
由②得$|\boldsymbol{a}|^{2}=4|\boldsymbol{b}|^{2}-3\boldsymbol{a}·\boldsymbol{b}$,代入①得$20|\boldsymbol{b}|^{2}+5\boldsymbol{a}·\boldsymbol{b}=900$。
则$\overrightarrow{AE}·\overrightarrow{CD}=(\frac{1}{6}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b})·(\frac{1}{2}\boldsymbol{a}-\boldsymbol{b})=\frac{1}{12}|\boldsymbol{a}|^{2}+\frac{1}{6}\boldsymbol{a}·\boldsymbol{b}-\frac{2}{3}|\boldsymbol{b}|^{2}=-\frac{1}{3}|\boldsymbol{b}|^{2}-\frac{1}{12}\boldsymbol{a}·\boldsymbol{b}=-\frac{1}{60}(20|\boldsymbol{b}|^{2}+5\boldsymbol{a}·\boldsymbol{b})=-15$。
多种解法一:如图,延长$AE$交$BC$于$F$,则$AF\perp BC$,过$D$作$DG\perp AF$于$G$,所以$\triangle CEF\sim\triangle DEG$。

设$EF = x$,则$\frac{EG}{EF}=\frac{DE}{EC}=\frac{2}{1}$,所以$EG = 2x$。又$D$为$AB$中点,$DG// BF$,所以$AG = FG = 3x$,所以$AE = AG + GE = 3x + 2x = 5$,解得$x = 1$,即$EF = 1$。
所以$\overrightarrow{AE}·\overrightarrow{CD}=\overrightarrow{AE}·3\overrightarrow{CE}=3|\overrightarrow{AE}||\overrightarrow{CE}|\cos\langle\overrightarrow{AE},\overrightarrow{CE}\rangle=3|\overrightarrow{AE}||\overrightarrow{CE}|(-\cos\angle CEF)=-3|\overrightarrow{AE}|·|\overrightarrow{EF}|=-15$。
多种解法二:延长$AE$交$BC$于$F$,则$AF\perp BC$。
$\overrightarrow{AE}·\overrightarrow{CD}=\overrightarrow{AE}·(\overrightarrow{CB}+\overrightarrow{BD})=\overrightarrow{AE}·\overrightarrow{CB}+\overrightarrow{AE}·\overrightarrow{BD}=0+\overrightarrow{AE}·(-\frac{1}{2}\overrightarrow{AB})=-\frac{1}{2}\overrightarrow{AE}·\overrightarrow{AB}$。
设$\overrightarrow{AE}$与$\overrightarrow{AB}$的夹角为$\theta$,则$\overrightarrow{AE}·\overrightarrow{CD}=-\frac{1}{2}·|\overrightarrow{AE}|·|\overrightarrow{AB}|\cos\theta=-\frac{1}{2}×5×|\overrightarrow{AF}|$。
设$\overrightarrow{AF}=\lambda\overrightarrow{AE}=\lambda(\frac{2}{3}\overrightarrow{AC}+\frac{1}{6}\overrightarrow{AB})=\frac{2}{3}\lambda\overrightarrow{AC}+\frac{\lambda}{6}\overrightarrow{AB}$,因为$B$,$F$,$C$三点共线,所以$\frac{2}{3}\lambda+\frac{\lambda}{6}=1$,解得$\lambda=\frac{6}{5}$。
所以$\overrightarrow{AF}=\frac{6}{5}\overrightarrow{AE}$,即$|\overrightarrow{AF}| = 6$,所以$\overrightarrow{AE}·\overrightarrow{CD}=-\frac{1}{2}×5×6=-15$。
二级结论:在$\triangle ABC$中,$D$为线段$BC$上一点,若$\frac{BD}{DC}=\frac{m}{n}$,则$\overrightarrow{AD}=\frac{m}{m + n}·\overrightarrow{AC}+\frac{n}{m + n}\overrightarrow{AB}$。
9. [全国甲理 2024·9,5 分]设向量$\boldsymbol{a} = (x + 1, x)$,$\boldsymbol{b} = (x, 2)$,则 (
A.$x = -3$是$\boldsymbol{a} \perp \boldsymbol{b}$的必要条件
B.$x = 1 + \sqrt{3}$是$\boldsymbol{a} // \boldsymbol{b}$的必要条件
C.$x = 0$是$\boldsymbol{a} \perp \boldsymbol{b}$的充分条件
D.$x = -1 + \sqrt{3}$是$\boldsymbol{a} // \boldsymbol{b}$的充分条件
C
)A.$x = -3$是$\boldsymbol{a} \perp \boldsymbol{b}$的必要条件
B.$x = 1 + \sqrt{3}$是$\boldsymbol{a} // \boldsymbol{b}$的必要条件
C.$x = 0$是$\boldsymbol{a} \perp \boldsymbol{b}$的充分条件
D.$x = -1 + \sqrt{3}$是$\boldsymbol{a} // \boldsymbol{b}$的充分条件
答案:
9.C [解析]因为$\boldsymbol{a}=(x + 1,x)$,$\boldsymbol{b}=(x,2)$,所以$\boldsymbol{a}\perp\boldsymbol{b}$的充要条件为$\boldsymbol{a}·\boldsymbol{b}=0$,即$(x + 1)· x + 2x = 0$,解得$x = 0$或$x = -3$,故A错误,C正确。$\boldsymbol{a}//\boldsymbol{b}$的充要条件为$2(x + 1)=x^{2}$,即$x^{2}-2x - 2 = 0$,解得$x = 1\pm\sqrt{3}$,故B,D错误。故选C。
10. [全国二 2025·12,5 分]已知平面向量$\boldsymbol{a} = (x, 1)$,$\boldsymbol{b} = (x - 1, 2x)$。若$\boldsymbol{a} \perp (\boldsymbol{a} - \boldsymbol{b})$,则$\vert\boldsymbol{a}\vert$ =
$\sqrt{2}$
。
答案:
10.$\sqrt{2}$ [解析]由题意得$\boldsymbol{a}-\boldsymbol{b}=(1,1 - 2x)$,由$\boldsymbol{a}\perp(\boldsymbol{a}-\boldsymbol{b})$,得$\boldsymbol{a}·(\boldsymbol{a}-\boldsymbol{b})=0$,即$x + 1 - 2x = 0$,所以$x = 1$,所以$\boldsymbol{a}=(1,1)$,故$|\boldsymbol{a}|=\sqrt{2}$。
多种解法:由$\boldsymbol{a}\perp(\boldsymbol{a}-\boldsymbol{b})$,得$\boldsymbol{a}·(\boldsymbol{a}-\boldsymbol{b})=0$,即$\boldsymbol{a}^{2}=\boldsymbol{a}·\boldsymbol{b}$,将$\boldsymbol{a}=(x,1)$,$\boldsymbol{b}=(x - 1,2x)$代入,得$x^{2}+1=x(x - 1)+2x$,解得$x = 1$,所以$\boldsymbol{a}=(1,1)$,故$|\boldsymbol{a}|=\sqrt{2}$。
多种解法:由$\boldsymbol{a}\perp(\boldsymbol{a}-\boldsymbol{b})$,得$\boldsymbol{a}·(\boldsymbol{a}-\boldsymbol{b})=0$,即$\boldsymbol{a}^{2}=\boldsymbol{a}·\boldsymbol{b}$,将$\boldsymbol{a}=(x,1)$,$\boldsymbol{b}=(x - 1,2x)$代入,得$x^{2}+1=x(x - 1)+2x$,解得$x = 1$,所以$\boldsymbol{a}=(1,1)$,故$|\boldsymbol{a}|=\sqrt{2}$。
查看更多完整答案,请扫码查看


