《2026年高中必刷题高中数学必修第二册人教版》

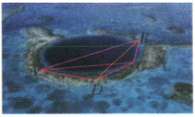
【例1】海洋蓝洞是地球罕见的自然地理现象，被誉为“地球给人类保留宇宙秘密的最后遗产”，我国拥有世界上已知最深的海洋蓝洞。若要测量如图所示的海洋蓝洞的口径(即 $ A,B $ 两点间的距离)，现取两点 $ C,D $，测得 $ CD = 80 $ 米，$ \angle ADB = 135^{\circ} $，$ \angle BDC = \angle ACD = 15^{\circ} $，$ \angle ACB = 120^{\circ} $，则图中海洋蓝洞的口径为$80\sqrt{5}$米。

答案： 解析：由已知得，在 $ \triangle ACD $ 中，$ \angle ACD = 15^{\circ} $，$ \angle ADC = 150^{\circ} $，所以 $ \angle DAC = 15^{\circ} $，由正弦定理得 $ AC = \frac{80×\sin150^{\circ}}{\sin15^{\circ}} = \frac{40}{\frac{\sqrt{6}-\sqrt{2}}{4}} = 40(\sqrt{6}+\sqrt{2}) $。
在 $ \triangle BCD $ 中，$ \angle BDC = 15^{\circ} $，$ \angle BCD = 135^{\circ} $，所以 $ \angle CBD = 30^{\circ} $，由正弦定理 $ \frac{CD}{\sin\angle CBD} = \frac{BC}{\sin\angle BDC} $，得 $ BC = \frac{CD·\sin\angle BDC}{\sin\angle CBD} = \frac{80×\sin15^{\circ}}{\frac{1}{2}} = 160×\sin15^{\circ} = 40(\sqrt{6}-\sqrt{2}) $。
在 $ \triangle ABC $ 中，由余弦定理，得 $ AB^{2} = AC^{2}+BC^{2}-2AC· BC·\cos120^{\circ} = 1600×(8 + 4\sqrt{3}) + 1600×(8 - 4\sqrt{3}) + 2×1600×(\sqrt{6}+\sqrt{2})×(\sqrt{6}-\sqrt{2})×\frac{1}{2} = 1600×16 + 1600×4 = 1600×20 = 32000 $，解得 $ AB = 80\sqrt{5} $。故图中海洋蓝洞的口径为 $ 80\sqrt{5} $ 米。
答案：$ 80\sqrt{5} $