《2026年高中必刷题高中数学必修第二册人教版》

8. [广东广州育才中学2025高一期中]已知$\triangle ABC$的内角$A$，$B$，$C$的对边分别为$a$，$b$，$c$，且$B = \frac{\pi}{4}$，$a = 2\sqrt{2}$，$b = 2\sqrt{5}$，则$AC$边上的高$h =$(B)

A.$\frac{3\sqrt{2}}{2}$
B.$\frac{6\sqrt{5}}{5}$
C.$\frac{5\sqrt{3}}{6}$
D.$\frac{7\sqrt{6}}{8}$

答案： 8.B　[解析]$\because B=\frac{\pi}{4}$，$a=2\sqrt{2}$，$b=2\sqrt{5}$，$\therefore$由余弦定理得$\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}$，即$\frac{\sqrt{2}}{2}=\frac{(2\sqrt{2})^{2}+c^{2}-(2\sqrt{5})^{2}}{2×2\sqrt{2}× c}$，解得$c = 6$或$c=-2$(舍去)。由三角形的面积公式可得$S_{\triangle ABC}=\frac{1}{2}bh=\frac{1}{2}ac\sin B$，即$h=\frac{ac\sin B}{b}=\frac{6\sqrt{5}}{5}$。故选B。

9. [河北石家庄2025高一期末]在$\triangle ABC$中，内角$A$，$B$，$C$所对的边分别是$a$，$b$，$c$。若$a\cos B + b\cos A = 4$，$AB$边上的高为$2\sqrt{3}$，则角$C$的最大值为(B)

A.$\frac{\pi}{4}$
B.$\frac{\pi}{3}$
C.$\frac{5\pi}{12}$
D.$\frac{7\pi}{12}$

答案：
9.B　[解析]由余弦定理得$a\cos B + b\cos A=\frac{a^{2}+c^{2}-b^{2}}{2c}+\frac{b^{2}+c^{2}-a^{2}}{2c}=c = 4$，又$AB$边上的高为$2\sqrt{3}$，$\therefore S_{\triangle ABC}=\frac{1}{2}×4×2\sqrt{3}=4\sqrt{3}$，$\therefore\frac{1}{2}ab\sin C=4\sqrt{3}$，$\therefore ab=\frac{8\sqrt{3}}{\sin C}$。$\because\cos C=\frac{a^{2}+b^{2}-c^{2}}{2ab}\geq\frac{2ab - c^{2}}{2ab}=1-\frac{8}{ab}$，当且仅当$a = b$时取等号，$\therefore\cos C\geq1-\frac{\sqrt{3}}{3}\sin C$，即$\frac{1}{2}\sin C+\frac{\sqrt{3}}{2}\cos C\geq\frac{\sqrt{3}}{2}$。$\because C\in(0,\pi)$，$\therefore C+\frac{\pi}{3}\in(\frac{\pi}{3},\frac{4\pi}{3})$，结合上式可得$C+\frac{\pi}{3}\in(\frac{\pi}{3},\frac{2\pi}{3}]$，$\therefore C\in(0,\frac{\pi}{3}]$，故角$C$的最大值为$\frac{\pi}{3}$。故选B。
归纳总结：在$\triangle ABC$中，$AD$是底边$BC$的高线，$D$为垂足。遇到高线问题，常见的处理方法有：
处理方法 处理思路
等面积法 $S_{\triangle ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}a\sin B=\frac{1}{2}b\sin A=\frac{1}{2}BC· AD$
三角函数在直角三角形中的定义 $\sin B=\frac{AD}{AB}$，$\cos B=\frac{BD}{AB}$，$\tan B=\frac{AD}{BD}$(也可利用角$C$)
勾股定理 $AB^{2}=AD^{2}+BD^{2}$，$AC^{2}=AD^{2}+CD^{2}$
射影定理 若$\triangle ABC$为直角三角形$(\angle BAC = 90^{\circ})$，$AD\perp BC$，则$AD^{2}=BD· CD$，$AB^{2}=BD· BC$，$AC^{2}=CD· BC$

10. [重庆巴蜀中学2025高一期末]在$\triangle ABC$中，内角$A$，$B$，$C$所对的边分别是$a$，$b$，$c$，且$a\cos C + \sqrt{3}a\sin C - b - c = 0$。
(1)求$A$的大小；
(2)若$AC$边的中线为$BE$，$BE = \frac{\sqrt{7}}{2}c$，$b = 6$，求$BC$边上的高。

答案： 10.[解]
(1)因为$a\cos C+\sqrt{3}a\sin C - b - c = 0$，所以由正弦定理得$\sin A\cos C+\sqrt{3}\sin A\sin C-\sin B-\sin C = 0$。又$A+B+C=\pi$，则$\sin B=\sin(\pi-A-C)=\sin(A + C)$，所以$\sin A\cos C+\sqrt{3}\sin A\sin C-\sin(A + C)-\sin C = 0$，所以$\sqrt{3}\sin A\sin C-\cos A\sin C-\sin C = 0$。又$C\in(0,\pi)$，则$\sin C\neq0$，可得$\sqrt{3}\sin A-\cos A = 1$，即$\sin(A-\frac{\pi}{6})=\frac{1}{2}$。因为$A\in(0,\pi)$，所以$A-\frac{\pi}{6}\in(-\frac{\pi}{6},\frac{5\pi}{6})$，所以$A-\frac{\pi}{6}=\frac{\pi}{6}$，所以$A=\frac{\pi}{3}$。
(2)在$\triangle ABE$中，$BE^{2}=AB^{2}+AE^{2}-2AB· AE·\cos A$，即$\frac{7}{4}c^{2}=c^{2}+9 - 3c$，解得$c = 2$(负值舍去)。又$a^{2}=b^{2}+c^{2}-2bc\cos A = 28$，解得$a = 2\sqrt{7}$。设$BC$边上的高为$h$，因为$S_{\triangle ABC}=\frac{1}{2}bc\sin A=\frac{1}{2}ah$，所以$\frac{1}{2}×6×2×\frac{\sqrt{3}}{2}=\frac{1}{2}×2\sqrt{7}· h$，可得$BC$边上的高$h=\frac{3\sqrt{21}}{7}$。

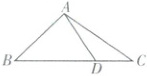
11. [江苏无锡2025高一期中]如图，在$\triangle ABC$中，已知$B = 45^{\circ}$，$D$是$BC$边上的一点，$AD = 5$，$AC = 7$，$DC = 3$，则$AB =$(D)


A.$4\sqrt{3}$
B.$5\sqrt{2}$
C.$2\sqrt{10}$
D.$\frac{5\sqrt{6}}{2}$

答案： 11.D　[解析]在$\triangle ACD$中，由余弦定理得$\cos C=\frac{AC^{2}+CD^{2}-AD^{2}}{2AC· CD}=\frac{49 + 9 - 25}{2×7×3}=\frac{11}{14}$，又因为$C\in(0,\pi)$，所以$\sin C=\sqrt{1-(\frac{11}{14})^{2}}=\frac{5\sqrt{3}}{14}$。在$\triangle ABC$中，由正弦定理得$\frac{AB}{\sin C}=\frac{AC}{\sin B}$，即$\frac{AB}{\frac{5\sqrt{3}}{14}}=\frac{7}{\frac{\sqrt{2}}{2}}$，解得$AB=\frac{5\sqrt{6}}{2}$。故选D。

12. [辽宁抚顺2025高一月考]如图，在四边形$ABCD$中，$\angle ADB = \angle DCA = 45^{\circ}$，$\angle BDC = 30^{\circ}$，$\angle BCA = 15^{\circ}$，$AB = 5\sqrt{5}$，则$CD$的长为(C)


A.$5\sqrt{3}$
B.$5\sqrt{5}$
C.$10\sqrt{3}$
D.$10\sqrt{5}$

答案： 12.C　[解析]因为$\angle BDC = 30^{\circ}$，$\angle BCD=15^{\circ}+45^{\circ}=60^{\circ}$，所以$\angle CBD = 90^{\circ}$。设$BC = x$，则$CD = 2x$，$BD=\sqrt{3}x$，在$\triangle ACD$中，$\angle DCA=45^{\circ}$，$\angle ADC=30^{\circ}+45^{\circ}=75^{\circ}$，故$\angle CAD = 60^{\circ}$，由正弦定理可得$\frac{AD}{\sin\angle DCA}=\frac{CD}{\sin\angle CAD}$，则$AD=\frac{CD\sin 45^{\circ}}{\sin 60^{\circ}}=\frac{2\sqrt{6}}{3}x$，在$\triangle ABD$中，由余弦定理可得$AB^{2}=AD^{2}+BD^{2}-2AD· BD\cos 45^{\circ}$，即$\frac{8}{3}x^{2}+3x^{2}-2·\frac{2\sqrt{6}}{3}x·\sqrt{3}x·\frac{\sqrt{2}}{2}=\frac{5}{3}x^{2}=125$，解得$x = 5\sqrt{3}$，故$CD = 2x = 10\sqrt{3}$。故选C。
归纳总结：多三角形问题指题目中涉及两个或多个三角形，通过公共边、公共角、位置关联(如拼接、嵌套)或几何条件(如共线、共圆)关联，需综合各三角形的边角关系求解，常见类型包括：
(1)共享边型：多个三角形共用一条边(如$\triangle ABC$与$\triangle ABD$共享边$AB$)；
(2)嵌套型：三角形包含于另一个三角形内(如$\triangle ABD$在$\triangle ABC$内部)；
(3)拼接型：多个三角形通过边拼接成多边形(如$\triangle ABC$与$\triangle ACD$拼接成四边形$ABCD$)；
(4)关联型：通过角度、边长比例或几何位置关联(如两个三角形的边平行、垂直或顶点共圆)；
(5)若三角形从顶角引出一线将三角形分为多个三角形，应注意利用公共角、公共边、补角等条件列方程；
(6)若知道点的具体位置，可利用向量表示。

13. 如图，在凸四边形$ABCD$中，$AB = 1$，$BC = \sqrt{3}$，$AC \perp CD$，$AC = CD$，当$\angle ABC$变化时，对角线$BD$的最大值为(D)


A.$3$
B.$4$
C.$\sqrt{7 + 2\sqrt{3}}$
D.$\sqrt{6} + 1$

答案： 13.D　[解析]设$\angle ABC=\alpha$，$\angle ACB=\beta$，则在$\triangle ABC$中，由余弦定理得$AC^{2}=4 - 2\sqrt{3}\cos\alpha$，所以$CD^{2}=4 - 2\sqrt{3}\cos\alpha$。由正弦定理得$\frac{AB}{\sin\beta}=\frac{AC}{\sin\alpha}$，则$\sin\beta=\frac{AB\sin\alpha}{AC}=\frac{\sqrt{3}\sin\alpha}{\sqrt{4 - 2\sqrt{3}\cos\alpha}}$。在$\triangle BCD$中，由余弦定理得$BD^{2}=BC^{2}+CD^{2}-2BC· CD\cos(\beta+\frac{\pi}{2})=3 + 4 - 2\sqrt{3}\cos\alpha - 2\sqrt{3}\sqrt{4 - 2\sqrt{3}\cos\alpha}\cos(\beta+\frac{\pi}{2})=7 + 2\sqrt{3}\sin\alpha - 2\sqrt{3}\cos\alpha=7 + 2\sqrt{6}\sin(\alpha-\frac{\pi}{4})$。又$\alpha\in(0,\pi)$，则$\alpha-\frac{\pi}{4}\in(-\frac{\pi}{4},\frac{3\pi}{4})$，所以当$\alpha-\frac{\pi}{4}=\frac{\pi}{2}$，即$\alpha=\frac{3\pi}{4}$时，$BD^{2}$取得最大值$7 + 2\sqrt{6}$，此时$BD=\sqrt{6}+1$。故选D。

14. (多选)[江西南昌江科附中2025高一期中]如图，已知圆$O$的内接四边形$ABCD$中，$AB = 2$，$BC = 6$，$AD = CD = 4$，下列说法正确的是(ACD)


A.四边形$ABCD$的面积为$8\sqrt{3}$
B.该外接圆的直径为$\frac{2\sqrt{21}}{3}$
C.$\overrightarrow{BO} · \overrightarrow{CD} = -4$
D.过$D$作$DF \perp BC$交$BC$于点$F$，则$\overrightarrow{DO} · \overrightarrow{DF} = 10$

答案：
14.ACD　[解析]对于A，如图①，连接$AC$，在$\triangle ACD$中，$\cos D=\frac{16 + 16 - AC^{2}}{32}$，在$\triangle ACB$中，$\cos B=\frac{4 + 36 - AC^{2}}{24}$，因为$B+D=\pi$，所以$\cos B+\cos D = 0$，故$\frac{40 - AC^{2}}{24}+\frac{32 - AC^{2}}{32}=0$，解得$AC^{2}=\frac{256}{7}$，所以$\cos D=-\frac{1}{7}$，$\cos B=\frac{1}{7}$，所以$\sin B=\sin D=\sqrt{1-\frac{1}{49}}=\frac{4\sqrt{3}}{7}$，故$S_{\triangle ABC}=\frac{1}{2}AB· BC\sin B=\frac{1}{2}×2×6×\frac{4\sqrt{3}}{7}=\frac{24\sqrt{3}}{7}$，$S_{\triangle ADC}=\frac{1}{2}AD· DC\sin D=\frac{1}{2}×4×4×\frac{4\sqrt{3}}{7}=\frac{32\sqrt{3}}{7}$，故四边形$ABCD$的面积为$\frac{24\sqrt{3}}{7}+\frac{32\sqrt{3}}{7}=8\sqrt{3}$，故A正确。

对于B，设外接圆半径为$R$，则$2R=\frac{AC}{\sin B}=\frac{\sqrt{\frac{256}{7}}}{\frac{4\sqrt{3}}{7}}=\frac{4\sqrt{21}}{3}$，故该外接圆的直径为$\frac{4\sqrt{21}}{3}$，半径为$\frac{2\sqrt{21}}{3}$，故B错误。
对于C，如图②，连接$BD$，过点$O$作$OG\perp CD$于点$G$，过点$B$作$BE\perp CD$于点$E$，则由垂径定理得$CG=\frac{1}{2}CD = 2$，因为$A+C=\pi$，所以$\cos A+\cos C = 0$，即$\frac{4 + 16 - BD^{2}}{16}+\frac{16 + 36 - BD^{2}}{48}=0$，解得$BD = 2\sqrt{7}$，所以$\cos C=\frac{1}{2}$，则$C=\frac{\pi}{3}$，且$CE=BC·\cos C = 6×\frac{1}{2}=3$，所以$|\overrightarrow{EG}|=3 - 2 = 1$，即$\overrightarrow{BO}$在向量$\overrightarrow{CD}$上的投影向量的模为$1$，且$\overrightarrow{EG}$与$\overrightarrow{CD}$反向，故$\overrightarrow{BO}·\overrightarrow{CD}=-|\overrightarrow{EG}|·|\overrightarrow{CD}|=-4$，故C正确。

对于D，如图③，由C选项可知$C=\frac{\pi}{3}$，故$|\overrightarrow{DF}|=CD·\sin\frac{\pi}{3}=4×\frac{\sqrt{3}}{2}=2\sqrt{3}$，且$\angle CDF=\frac{\pi}{6}$。因为$AD = CD$，故$DO$为$\angle ADC$的平分线，故$\angle ODF=\frac{1}{2}\angle ADC-\frac{\pi}{6}$。由A选项可知$\cos\angle ADC=-\frac{1}{7}$，显然$\frac{1}{2}\angle ADC$为锐角，故$\cos\frac{1}{2}\angle ADC=\sqrt{\frac{1+\cos\angle ADC}{2}}=\frac{\sqrt{21}}{7}$，$\sin\frac{1}{2}\angle ADC=\sqrt{1 - (\frac{\sqrt{21}}{7})^{2}}=\frac{2\sqrt{7}}{7}$，所以$\cos\angle ODF=\cos(\frac{1}{2}\angle ADC-\frac{\pi}{6})=\cos\frac{1}{2}\angle ADC\cos\frac{\pi}{6}+\sin\frac{1}{2}\angle ADC\sin\frac{\pi}{6}=\frac{\sqrt{21}}{7}·\frac{\sqrt{3}}{2}+\frac{2\sqrt{7}}{7}·\frac{1}{2}=\frac{5\sqrt{7}}{14}$，所以$\overrightarrow{DO}·\overrightarrow{DF}=|\overrightarrow{DO}|·|\overrightarrow{DF}|·\cos\angle ODF=\frac{2\sqrt{21}}{3}×2\sqrt{3}×\frac{5\sqrt{7}}{14}=10$，故D正确。

故选ACD。

15. 如图，在$\triangle ABC$中，$\angle BAC = \frac{3\pi}{4}$，$AB = AC$，$D$，$E$是边$BC$上的两点，且$\angle BAD = \angle DAE = \angle EAC$，则$\frac{DE}{BC} =$3 - 2\sqrt{2}。

答案： 15.3 - 2\sqrt{2}　[解析]因为$\angle BAC=\frac{3\pi}{4}$，$AB = AC$，所以$\angle ABC=\angle ACB=\frac{\pi}{8}$。不妨设$AB = m$，则$BC^{2}=AB^{2}+AC^{2}-2AB· AC\cos\angle BAC=(2+\sqrt{2})m^{2}$。因为$\angle BAD=\angle DAE=\angle EAC$，所以$\angle BAE=\frac{2}{3}\angle BAC=\frac{\pi}{2}$，所以$BE=\frac{AB}{\cos\angle ABC}=\frac{m}{\cos\frac{\pi}{8}}$，同理可得$CD=\frac{m}{\cos\frac{\pi}{8}}$。因为$BE + CD = BC + DE$，所以$DE = 2BE - BC$，故$\frac{DE}{BC}=\frac{2BE}{BC}-1$。由二倍角的余弦公式可得$\cos\frac{\pi}{4}=2\cos^{2}\frac{\pi}{8}-1$，可得$\cos\frac{\pi}{8}=\sqrt{\frac{1+\cos\frac{\pi}{4}}{2}}=\sqrt{\frac{2+\sqrt{2}}{4}}=\frac{\sqrt{2+\sqrt{2}}}{2}$，所以$\frac{DE}{BC}=\frac{2BE}{BC}-1=\frac{\frac{2m}{\cos\frac{\pi}{8}}}{\sqrt{(2 + \sqrt{2})m^{2}}}-1=\frac{4}{2+\sqrt{2}}-1=3 - 2\sqrt{2}$。