2026年高中必刷题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年高中必刷题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 下列说法中正确的有(
①在物理学中,作用力与反作用力是一对共线向量;
②温度有零上温度和零下温度,因此温度也是向量;
③方向为南偏西 $60^{\circ}$ 的向量与北偏东 $60^{\circ}$ 的向量是共线向量;
④平面上的数轴都是向量.
A.1 个
B.2 个
C.3 个
D.4 个
B
)①在物理学中,作用力与反作用力是一对共线向量;
②温度有零上温度和零下温度,因此温度也是向量;
③方向为南偏西 $60^{\circ}$ 的向量与北偏东 $60^{\circ}$ 的向量是共线向量;
④平面上的数轴都是向量.
A.1 个
B.2 个
C.3 个
D.4 个
答案:
1.B【解析】既有大小又有方向的量称为向量,结合向量的概念可知②④错误,结合向量的概念以及共线向量的定义可知①③正确,故选B。
2. [广东佛山 2025 高一质检 ] 在菱形 $ABCD$ 中,$\angle DAB = 120^{\circ}$,对角线 $AC \cap BD = O$,给出以下结论:
①$\overrightarrow{DO}$ 与 $\overrightarrow{DB}$ 是平行向量;
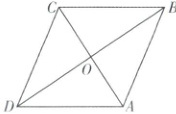
②$\overrightarrow{DA}$ 与 $\overrightarrow{BC}$ 是共线向量;
③$|\overrightarrow{DC}| = |\overrightarrow{AC}|$;
④$\overrightarrow{DO}$ 与 $\overrightarrow{AB}$ 是共线向量.
其中正确结论的个数是(
A.1
B.2
C.3
D.4
①$\overrightarrow{DO}$ 与 $\overrightarrow{DB}$ 是平行向量;

②$\overrightarrow{DA}$ 与 $\overrightarrow{BC}$ 是共线向量;
③$|\overrightarrow{DC}| = |\overrightarrow{AC}|$;
④$\overrightarrow{DO}$ 与 $\overrightarrow{AB}$ 是共线向量.
其中正确结论的个数是(
C
)A.1
B.2
C.3
D.4
答案:
2.C【解析】对于①,因为DO和DB在同一条直线上,根据平行向量的定义,平行向量又称共线向量,方向相同或相反,①正确;对于②,因为四边形ABCD是菱形,所以AD//BC,根据平行向量的定义,平行向量又称共线向量,方向相同或相反,②正确;对于③,在菱形ABCD中,∠DAB = 120°,所以△ACD为等边三角形,则AC = DC,所以|DC| = |AC|,③正确;对于④,DO与AB不平行,所以DO与AB不共线,④错误。故选C。
3. [北京通州区 2025 高一期中 ] 已知平面向量 $a$,$b$,则“$a = b$”是“$|a| = |b|$”的(
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
A
)A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:
3.A【解析】若a = b,则|a| = |b|,反过来,若|a| = |b|,两个向量的方向不确定,不能推出a = b,所以“a = b”是“|a| = |b|”的充分不必要条件。故选A。
4. [河南郑州一中 2025 高一期中 ] 已知点 $O$ 在 $\triangle ABC$ 所在平面内,且满足 $|\overrightarrow{OA}| = |\overrightarrow{OB}| = |\overrightarrow{OC}|$,则点 $O$ 是 $\triangle ABC$ 的(
A.外心
B.内心
C.垂心
D.重心
A
)A.外心
B.内心
C.垂心
D.重心
答案:
4.A【解析】因为|OA| = |OB| = |OC|,即点O到点A,B,C的距离相等,所以点O是△ABC的外心,故选A。
5. [安徽蚌埠 2025 高一月考 ] 在四边形 $ABCD$ 中,$AC$ 与 $BD$ 交于点 $O$,且 $\overrightarrow{AO} = \overrightarrow{OC}$,$\overrightarrow{BO} = \overrightarrow{OD}$,$|\overrightarrow{AC}| = |\overrightarrow{BD}|$,则(
A.$AC \perp BD$
B.四边形 $ABCD$ 是梯形
C.四边形 $ABCD$ 是菱形
D.四边形 $ABCD$ 是矩形
D
)A.$AC \perp BD$
B.四边形 $ABCD$ 是梯形
C.四边形 $ABCD$ 是菱形
D.四边形 $ABCD$ 是矩形
答案:
5.D【解析】由AO = OC,BO = OD,|AC| = |BD|,知四边形ABCD的对角线互相平分且相等,所以四边形ABCD为矩形。故选D。
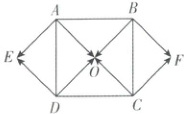
6. 如图所示,$O$ 为正方形 $ABCD$ 对角线的交点,四边形 $OAED$,$OCFB$ 都是正方形,根据图中所标出的向量回答下列问题.
(1) 分别写出与 $\overrightarrow{AO}$,$\overrightarrow{BO}$ 相等的向量;
(2) 写出与 $\overrightarrow{AO}$ 共线的向量;
(3) 写出与 $\overrightarrow{AO}$ 模相等的向量.
(1) 分别写出与 $\overrightarrow{AO}$,$\overrightarrow{BO}$ 相等的向量;
(2) 写出与 $\overrightarrow{AO}$ 共线的向量;
(3) 写出与 $\overrightarrow{AO}$ 模相等的向量.

答案:
6.【解】
(1)AO = BF,BO = AE。
(2)与AO共线的向量有CO,BF,DE。
(3)与AO模相等的向量有CO,BF,DE,AE,BO,DO,CF。
(1)AO = BF,BO = AE。
(2)与AO共线的向量有CO,BF,DE。
(3)与AO模相等的向量有CO,BF,DE,AE,BO,DO,CF。
7. 如图所示的方格纸是由若干个边长为 1 的小正方形拼在一起组成的,方格纸中有两个定点 $A$,$B$,点 $C$ 为小正方形的顶点,且 $|\overrightarrow{AC}| = \sqrt{5}$.
(1) 画出所有满足条件的向量 $\overrightarrow{AC}$;
(2) 求 $|\overrightarrow{BC}|$ 的最大值与最小值.

(1) 画出所有满足条件的向量 $\overrightarrow{AC}$;
(2) 求 $|\overrightarrow{BC}|$ 的最大值与最小值.

答案:
7.【解】
(1)画出所有满足条件的向量ACᵢ(i = 1,2,…,8),如图所示。

(2)由
(1)所画的图知,当点C位于点C₁或C₂的位置时,|BC|取得最小值$\sqrt{1² + 2²}$ = $\sqrt{5}$;当点C位于点C₅或C₆的位置时,|BC|取得最大值$\sqrt{4² + 5²}$ = $\sqrt{41}$,故|BC|的最大值为$\sqrt{41}$,最小值为$\sqrt{5}$。
7.【解】
(1)画出所有满足条件的向量ACᵢ(i = 1,2,…,8),如图所示。

(2)由
(1)所画的图知,当点C位于点C₁或C₂的位置时,|BC|取得最小值$\sqrt{1² + 2²}$ = $\sqrt{5}$;当点C位于点C₅或C₆的位置时,|BC|取得最大值$\sqrt{4² + 5²}$ = $\sqrt{41}$,故|BC|的最大值为$\sqrt{41}$,最小值为$\sqrt{5}$。
查看更多完整答案,请扫码查看


