《2026年高中必刷题高中数学必修第二册人教版》

1. [山西朔州 2025 高一月考]在某测量中，设点 A 在点 B 的南偏东 $34^{\circ}27'$ 方向上，则点 B 在点 A 的(A)

A.北偏西 $34^{\circ}27'$ 方向上
B.北偏东 $55^{\circ}33'$ 方向上
C.北偏西 $55^{\circ}32'$ 方向上
D.南偏西 $55^{\circ}33'$ 方向上

答案：
1.A [解析]如图所示:

因为点A在点B的南偏东$34^{\circ}27'$方向上，所以点B在点A的北偏西$34^{\circ}27'$方向上.故选A.

2. 如图，前卫斜塔位于辽宁省葫芦岛市绥中县，始建于辽代，又名瑞州古塔，其倾斜度(塔与地面所成的角)远超著名的意大利比萨斜塔. 现有一个斜塔的塔身长 10 m，一旅游者在正午时分(太阳光线与地面垂直)测得塔在地面上的投影长为 5 m，则该塔的倾斜度(塔与地面所成的角)为(A)

A.$60^{\circ}$
B.$45^{\circ}$
C.$30^{\circ}$
D.$15^{\circ}$

答案：
2.A　[解析]如图所示，线段AC表示塔身，线段AB为塔在地面上的投影，$CB\perp AB$，所以在$Rt\triangle ABC$中，$\cos A=\frac{AB}{AC}=\frac{1}{2}$.
因为$0^{\circ}＜A＜90^{\circ}$，所以$A = 60^{\circ}$，故选A.

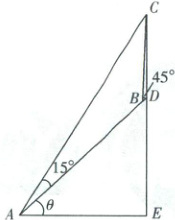
3. [江苏盐城 2024 高一期中]如图所示，在坡度一定的山坡 A 处测得山顶上一建筑物 CD 的顶端 C 对于山坡的斜度为 $15^{\circ}$，向山顶前进 100 m 到达 B 处，又测得 C 对于山坡的斜度为 $45^{\circ}$. 若 $CD = 50$ m，山坡对于地平面的坡度为 $\theta$，则 $\cos\theta =$(C)

A.$\dfrac{\sqrt{3}}{2}$
B.$\dfrac{\sqrt{2}}{2}$
C.$\sqrt{3}-1$
D.$\sqrt{2}-1$

答案： 3.C [解析]由题意得$\angle ACB = 30^{\circ}$，在$\triangle ABC$中，由正弦定理得$\frac{AB}{\sin 30^{\circ}}=\frac{AC}{\sin 135^{\circ}}$，
点悟：$\angle ACB=\angle CBD - \angle CAB = 30^{\circ}$
$\therefore AC = 100\sqrt{2}$.
在$\triangle ADC$中，$\frac{AC}{\sin(\theta + 90^{\circ})}=\frac{CD}{\sin 15^{\circ}}$，
$\therefore \cos\theta=\sin(\theta + 90^{\circ})=\frac{AC·\sin 15^{\circ}}{CD}=\sqrt{3}-1$.故选C.

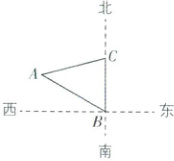
4. [河北保定 2024 高一期中]如图，一艘船航行到点 B 处时，测得灯塔 A 在其北偏西 $60^{\circ}$ 的方向上，随后该船以 20 海里/时的速度，往正北方向航行两小时后到达点 C，测得灯塔 A 在其南偏西 $75^{\circ}$ 的方向上，此时船与灯塔 A 间的距离为(C)

A.$20\sqrt{3}$ 海里
B.$40\sqrt{3}$ 海里
C.$20\sqrt{6}$ 海里
D.$40\sqrt{6}$ 海里

答案： 4.C [解析]依题意，在$\triangle ABC$中，$B = 60^{\circ}$，$C = 75^{\circ}$，则$A = 45^{\circ}$，而$BC = 40$，由正弦定理得$\frac{AC}{\sin B}=\frac{BC}{\sin A}$，则$AC=\frac{BC\sin B}{\sin A}=\frac{40\sqrt{3}}{\frac{\sqrt{2}}{2}}=20\sqrt{6}$，所以船与灯塔A间的距离为$20\sqrt{6}$海里.故选C.
规律方法此类问题的解决方法
首先根据已知确定所构造的三角形有关的边和角，再通过解三角形求相应的距离.利用正弦定理解决距离问题时，通常需测出所构造三角形的两角和一边；利用余弦定理解决距离问题时，通常需要测出所构造三角形的两边和一角，有时需综合运用两个定理求解.

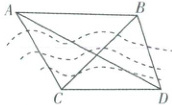
5. 教材变式 [山东潍坊 2025 高一月考]为加快推进“5G+光网”双千兆城市建设，如图，在东北某地地面有四个 5G 基站 A，B，C，D. 已知 C，D 两个基站建在松花江的南岸，距离为 $10\sqrt{3}$ km；基站 A，B 在江的北岸，测得 $\angle ACB = 75^{\circ}$，$\angle ACD = 120^{\circ}$，$\angle ADC = 30^{\circ}$，$\angle ADB = 45^{\circ}$，则 A，B 两个基站的距离为(D)

A.$10\sqrt{6}$ km
B.$30(\sqrt{3}-1)$ km
C.$30(\sqrt{2}-1)$ km
D.$10\sqrt{5}$ km

答案： 5.D
思路导引根据题意可得$AC = CD = 10\sqrt{3}$，$\angle CBD = 60^{\circ}$，利用正弦定理求出$BC$，进而结合余弦定理即可求出$AB$.
[解析]在$\triangle ACD$中，$\angle ADC = 30^{\circ}$，$\angle ACD = 120^{\circ}$，所以$\angle CAD = 30^{\circ}$，
所以$AC = CD = 10\sqrt{3}$.
又$\angle ACB = 75^{\circ}$，所以$\angle BCD = 45^{\circ}$，
在$\triangle BDC$中，$\angle CDB = 75^{\circ}$，$\angle CBD = 180^{\circ}-(75^{\circ}+45^{\circ}) = 60^{\circ}$，由正弦定理，得$\frac{BC}{\sin\angle CDB}=\frac{CD}{\sin\angle CBD}$，则$BC=\frac{10\sqrt{3}\sin 75^{\circ}}{\sin 60^{\circ}}=5\sqrt{2}+5\sqrt{6}$.
在$\triangle ABC$中，由余弦定理，得
$AB^{2}=AC^{2}+BC^{2}-2AC· BC\cos\angle ACB=(10\sqrt{3})^{2}+(5\sqrt{2}+5\sqrt{6})^{2}-2×10\sqrt{3}×(5\sqrt{2}+5\sqrt{6})×\frac{\sqrt{6}-\sqrt{2}}{4}=500$，所以$AB = 10\sqrt{5}$，即
A，B两个基站之间的距离为$10\sqrt{5}\ km$.故选D.
链接教材本题是教材第49页例9的同类试题，考查实际问题中的距离测算和解三角形的实际应用.解题的关键将实际问题抽象成数学问题，将已知量与未知量全部集中在一个或几个三角形中，可用余弦定理或正弦定理求解.
归纳总结解三角形的应用问题时，将实际问题抽象概括后，通常会遇到两种情况：
(1)已知量与未知量全部集中在一个三角形中，这时利用正弦定理或余弦定理求解即可.
(2)已知量与未知量涉及两个或两个以上的三角形，这时需先作出这些三角形，选择条件充足的三角形优先研究，再逐步在其余的三角形中求出问题的解.有时需设出未知量，在几个三角形中列出方程，解方程得出所要求的解.

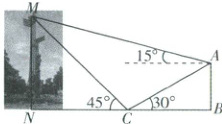
6. [安徽蚌埠 2025 高一期末]如图，南北分界线是蚌埠的标志性建筑，小明为了测量其高度 MN，在地面上选择一个观测点 C，在 C 处测得 A 处的无人机和该建筑的最高点 M 的仰角分别为 $30^{\circ}$，$45^{\circ}$，无人机距地面的高度 AB 为 20 米，且在 A 处无人机测得点 M 的仰角为 $15^{\circ}$，点 B，C，N 在同一条直线上，则该建筑的高度 MN(单位：米)为(D)

A.$20\sqrt{3}$
B.$25\sqrt{3}$
C.$\dfrac{40\sqrt{3}}{3}$
D.40

答案： 6.D　[解析]在$Rt\triangle ABC$中，$\angle ACB = 30^{\circ}$，$AB = 20$，则$AC = 2AB = 40$.
由题图可知$\angle MAC = 45^{\circ}$，$\angle MCA = 180^{\circ}-45^{\circ}-30^{\circ}=105^{\circ}$，则$\angle CMA = 180^{\circ}-45^{\circ}-105^{\circ}=30^{\circ}$.
在$\triangle AMC$中，由正弦定理$\frac{AC}{\sin\angle AMC}=\frac{MC}{\sin\angle CAM}$，得$MC=\frac{40×\frac{\sqrt{2}}{2}}{\frac{1}{2}}=40\sqrt{2}$.
在$Rt\triangle MNC$中，$MN = MC·\sin 45^{\circ}=40\sqrt{2}×\frac{\sqrt{2}}{2}=40$.故选D.

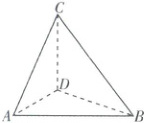
7. [浙江宁波 2025 高一期末]某学生为测量宁波天封塔的高度，如图，选取了与天封塔底部 D 在同一水平面上的 A，B 两点，测得 $AB = 50\sqrt{7}$ 米，在 A，B 两点观察塔顶 C 点，仰角分别为 $45^{\circ}$ 和 $30^{\circ}$，且 $\angle ADB = 150^{\circ}$，则宁波天封塔的高度 CD(单位：米)是(A)

A.50
B.$40\sqrt{3}$
C.$30\sqrt{7}$
D.$50\sqrt{7}$

答案： 7.A　[解析]设$CD = x$，由$\angle CAD = 45^{\circ}$，$\angle CBD = 30^{\circ}$，得$AD = x$，$BD = \sqrt{3}x$.在$\triangle ADB$中，$\angle ADB = 150^{\circ}$，由余弦定理得$(50\sqrt{7})^{2}=x^{2}+(\sqrt{3}x)^{2}-2x·\sqrt{3}x·(-\frac{\sqrt{3}}{2})$，解得$x = 50$.
避坑：注意$\cos 150^{\circ}=-\cos 30^{\circ}$，勿漏掉负号
所以宁波天封塔的高度$CD$是50米.故选A.