《2026年高中必刷题高中数学必修第二册人教版》

1. 共同富裕是全体人民通过辛勤劳动和相互帮助最终达到丰衣足食的生活水平，是消除两极分化和贫穷基础上的普遍富裕. 下列关于个人收入的统计量中，最能体现共同富裕要求的是(D)

A.平均数小，方差大
B.平均数小，方差小
C.平均数大，方差大
D.平均数大，方差小

答案： 1. D 【解析】方差反映的是一组数据的波动情况，方差越大说明数据偏离平均水平的程度越大，平均数是整体的平均水平，是一组数据的集中程度的刻画，所以最能体现共同富裕要求的是平均数大，方差小. 故选D.
规律方法 标准差、方差描述了一组数据围绕平均数波动的大小. 标准差或方差越大，数据的离散程度越大；标准差或方差越小，数据的离散程度越小.

2. (多选)[重庆巴蜀中学 2025 高一期中]校园合唱比赛中，高一(4)班演唱结束后，10 位裁判分别进行打分，结果如下(满分 10 分):9.0，8.8，9.0，9.2，9.3，8.9，8.8，9.0，8.5，9.5，则下列说法正确的是(ABD)

A.该班的平均得分是 9.0 分
B.该班得分的第 70 百分位数是 9.1 分
C.该班得分的方差是 0.72
D.若得分数据去掉一个最高分和一个最低分后，该班得分的平均分不变，标准差变小

答案： 2. ABD 【解析】把得分按从小到大排列：8.5,8.8,8.8,8.8,8.9,9.0,9.0,9.0,9.2,9.3,9.5.
对于A：平均分为$\frac{1}{10} × (8.5+8.8+8.8+8.8+8.9+9.0+9.0+9.0+9.2+9.3+9.5)=9.0，$故A正确；
对于B：因为10 × 0.7=7，故第70百分位数为$\frac{9.0+9.2}{2}=9.1，$故B正确；
对于C：方差为$\frac{1}{10} × [(8.5 - 9)^2 + 2 × (8.8 - 9)^2 + (8.9 - 9)^2 + 3 × (9.0 - 9)^2 + (9.2 - 9)^2 + (9.3 - 9)^2 + (9.5 - 9)^2]=0.072，$故C错误；
对于D：由于最高分和最低分的平均数是9，故平均分不变，去掉后，数据更集中，故标准差变小，D正确. 故选ABD.
![img alt=规律方法] 一组数据$x_1,x_2,·s,x_n$的方差为$\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 = \frac{1}{n} \sum_{i=1}^{n} x_i^2 - \bar{x}^2，$标准差为$\sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2}.$

3. [江苏南京五校 2025 高一期末]若甲组样本数据 $ x_1,x_2,·s,x_n $ (数据各不相同)的平均数为 2，方差为 5，乙组样本数据 $ 3x_1 + a,3x_2 + a,·s,3x_n + a $ 的平均数为 5，则下列说法不正确的是(D)

A.$ a $ 的值为 -1
B.乙组样本数据的方差为 45
C.两组样本数据的样本极差不同
D.两组样本数据的样本中位数一定相同

答案： 3. D 【解析】由甲组样本数据$x_1,x_2,·s,x_n（$数据各不相同）的平均数$\bar{x}=2，$方差$s^2=5，$
乙组样本数据$3x_1+a,3x_2+a,·s,3x_n+a$的平均数为5，
可得$3\bar{x}+a=5，$即3 × 2+a=5，解得a=-1，所以A正确；
设乙组样本数据的方差为$s_1^2，$可得$s_1^2=3^2 × s^2=45，$所以B正确；
不妨设$x_1＜x_2＜·s＜x_n，$则甲组数据的极差为$x_n - x_1，$
乙组数据的极差为$(3x_n+a)-(3x_1+a)=3(x_n - x_1)，$
因为甲组数据各不相同，所以两组样本数据的极差不相等，所以C正确；
设甲组样本数据的中位数为m，则乙组样本数据的中位数为3m - 1，
若m=3m - 1，可得$m=\frac{1}{2}，$所以两组样本数据的中位数可能相同，所以D不正确.
故选D.
规律方法 若$x_1,x_2,·s,x_n$的平均数为$\bar{x}，$方差为$s^2，$则$mx_1+a,mx_2+a,·s,mx_n+a$的平均数是$m\bar{x}+a，$方差是$m^2s^2.$

4. 为了了解各学科的成绩情况，从所有考生成绩中随机抽出 20 位考生的成绩进行统计分析，其中数学成绩的频率分布直方图如图所示. 据此估计，在本次考试中数学成绩的方差为110. (同一组中的数据用该组区间的中点值作代表)

答案： 4. 110 【解析】根据题中频率分布直方图，得该组数据的平均数$\bar{x}=55 × 0.010 × 10+65 × 0.020 × 10+75 × 0.035 × 10+85 × 0.030 × 10+95 × 0.005 × 10=75，$
则方差$s^2=(75 - 55)^2 × 0.10+(75 - 65)^2 × 0.20+(75 - 75)^2 × 0.35+(75 - 85)^2 × 0.30+(75 - 95)^2 × 0.05=110.$
归纳总结 根据频率分布直方图求一组数据的方差的方法：先利用各组区间的中点值乘频率（即每组矩形的面积）求和得$\bar{x}，$再将平均数减去每组区间的中点值平方后乘该组的频率求和.

5. 教材变式 甲、乙两名射击运动员在某次比赛中各射击 6 次，得到的环数如下表所示：

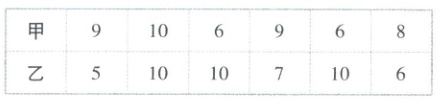
(1)分别求出甲、乙运动员 6 次射击环数的平均数；
(2)分别求出甲、乙运动员这 6 次射击数据的方差，并根据计算结果说明本次比赛哪位运动员的发挥更稳定.

答案： 5. 【解】
(1)由甲、乙运动员的6次射击成绩可得，
甲6次射击环数的平均数$\bar{x}_1=\frac{1}{6} × (9+10+6+9+6+8)=8，$
乙6次射击环数的平均数$\bar{x}_2=\frac{1}{6} × (5+10+10+7+10+6)=8.$
(2)由
(1)可知甲、乙运动员6次射击环数的平均数均为8，则甲6次射击环数的方差$s_1^2=\frac{1}{6} × [(9 - 8)^2+(10 - 8)^2+(6 - 8)^2+(9 - 8)^2+(6 - 8)^2+(8 - 8)^2]=\frac{14}{6}=\frac{7}{3}$
乙6次射击环数的方差$s_2^2=\frac{1}{6} × [(5 - 8)^2+(10 - 8)^2+(10 - 8)^2+(7 - 8)^2+(10 - 8)^2+(6 - 8)^2]=\frac{26}{6}=\frac{13}{3}$
由于$s_1^2=\frac{7}{3}＜s_2^2=\frac{13}{3}，$因此本次比赛甲运动员的发挥更稳定.
链接教材 本题是教材第211页问题3的同类题目，考查平均数与方差在实际生活中的应用. 数据$x_1,x_2,·s,x_n$的平均数$\bar{x}=\frac{x_1+x_2+·s+x_n}{n}，$方差$s^2=\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2.$
方差刻画的是数据的离散程度，在平均数相等的情况下，方差越小，数据越稳定.
归纳总结 总体方差和标准差
(1)总体方差和标准差：若总体中所有个体的变量值分别为$Y_1,Y_2,·s,Y_N，$总体的平均数为$\bar{Y}，$则称$S^2=\frac{1}{N} \sum_{i=1}^{N} (Y_i - \bar{Y})^2$为总体方差，$S=\sqrt{S^2}$为总体标准差.
(2)总体方差的加权形式：若总体的N个变量值中，不同的值共有$k(k \leq N)$个，不妨记为$Y_1,Y_2,·s,Y_k，$其中Y_i出现的频数为f_i(i=1,2,·s,k)，
则总体方差为$S^2=\frac{1}{N} \sum_{i=1}^{k} f_i(Y_i - \bar{Y})^2.$

6. (多选)[吉林长春 2025 高一期中]某研究机构在训练人工智能模型时，有两种训练算法甲和乙，使用算法甲训练了 30 次，每次训练耗时的平均数为 2，方差为 0.25，使用算法乙训练了 20 次，每次训练耗时的平均数为 1.5，方差为 0.3，则(AD)

A.总体每次训练平均耗时 1.8 小时
B.总体每次训练平均耗时 1.75 小时
C.总体每次训练耗时的方差为 0.28
D.总体每次训练耗时的方差为 0.33

答案： 6. AD 【解析】总体每次训练平均耗时$\bar{x}=\frac{30 × 2+20 × 1.5}{30+20}=\frac{60+30}{50}=1.8，$故A正确，B错误；总体每次训练耗时的方差$s^2=\frac{30}{50} × [0.25+(2 - 1.8)^2]+\frac{20}{50} × [0.3+(1.5 - 1.8)^2]=\frac{30 × 0.29+20 × 0.39}{50}=\frac{8.7+7.8}{50}=\frac{16.5}{50}=0.33，$故C错误，D正确. 故选AD.

7. 教材变式 某校高一(1)班有男生 20 人、女生 30 人. 已知某次数学测验中，男生成绩的平均数为 100，方差为 11，女生成绩的平均数为 95，方差为 16，则这次测验中班级总体成绩的方差为20.

答案： 7. 20 【解析】依题意得，这次测验中班级总体成绩的平均数为$\frac{20}{20+30} × 100+\frac{30}{20+30} × 95=97，$方差为$\frac{20}{20+30} × [(100 - 97)^2+11]+\frac{30}{20+30} × [(95 - 97)^2+16]=20.$
链接教材 本题是教材第213页例6的同类试题，考查按比例分配的分层随机抽样方差的计算.
设样本中不同层的平均数分别为$\bar{x}_1,\bar{x}_2,·s,\bar{x}_n，$方差分别为$s_1^2,s_2^2,·s,s_n^2，$相应的权重分别为$\omega_1,\omega_2,·s,\omega_n，$则总样本的方差$s^2=\sum_{i=1}^{n} \omega_i[s_i^2+(\bar{x}_i - \bar{x})^2]，$其中$\bar{x}$为总样本平均数.

8. 已知一组样本数据 $ x_1,x_2,·s,x_{10} $，且 $ x_1^2 + x_2^2 + ·s + x_{10}^2 = 2022 $，平均数 $ \overline{x} = 12 $，则该组数据的方差为58.2.

答案： 8.58.2 【解析】因为一组样本数据为$x_1,x_2,·s,x_{10}，$且$x_1^2+x_2^2+·s+x_{10}^2=2022，$平均数$\bar{x}=12，$
所以该组数据的方差为$\frac{1}{10} [(x_1 - 12)^2+(x_2 - 12)^2+·s+(x_{10} - 12)^2]=\frac{1}{10} [(x_1^2+x_2^2+·s+x_{10}^2)-24(x_1+x_2+·s+x_{10})+10 × 12^2]=\frac{1}{10} × (2022 - 24 × 10 × 12+10 × 144)=58.2.$
易错警示 本题中由于已知条件中含$x_1^2+x_2^2+·s+x_{10}^2=2022，$若直接利用方差公式$\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2，$则不能求解，因此需要将方差公式变形为$s^2=\frac{1}{n} [(x_1^2+x_2^2+·s+x_n^2)-n\bar{x}^2]$或写成$s^2=\frac{1}{n} (x_1^2+x_2^2+·s+x_n^2)-\bar{x}^2$后结合已知条件求方差.