《2026年高中必刷题高中物理必修第二册人教版》

1. [广东湛江2025高一下期中]通常情况下，越靠近河岸，河水的流速越小.若一小船从南岸到北岸横渡一条河，小船的静水速度大小、方向均不变(船头方向垂直于河岸)，则在下列四幅图中，能表示小船渡河的轨迹的是(C)

答案： 1.C　[解析]根据题意可知，从南岸到北岸，河水的流速先增大后减小，又小船在垂直河岸方向上做匀速直线运动，故小船的合速度与河岸方向的夹角先减小后增大，结合合速度方向（关键点：找出小船的合速度方向，即对地的速度方向沿运动轨迹的切线方向），可知小船渡河过程中的运动轨迹应先向下游弯曲，后向上游弯曲，C正确。

2. [陕西西安长安区一中2025高一下期中]我国某款无人艇装上相控阵雷达.如图所示，该无人艇位于与对岸的最近距离为20$\sqrt 3$ m的O点处，从O点向下游20m处有一危险区，当时水流速度为17$\sqrt 3$ m/s，为了使无人艇避开危险区沿直线到达对岸，无人艇在静水中的速度大小至少为(C)


A.20 m/s
B.20$\sqrt 3$ m/s
C.25.5 m/s
D.50 m/s

答案：
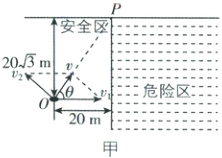
2.C　[解析]若无人艇刚好避开危险区，如图甲所示，设无人艇沿OP方向以速度v行驶，水流速度为$v_1$，由几何知识得（破点：合速度沿OP方向时恰好避开危险区）
$\tan \theta = \frac{20\sqrt{3}}{20} = \sqrt{3}$，所以$\theta = 60°$，当无人艇在静水中的速度$v_2 \perp v$时，$v_2$最小，$v_2 = v_1 \sin \theta = 17\sqrt{3} × \frac{\sqrt{3}}{2} m/s = 25.5 m/s$，显然无人艇沿其他方向行驶时，如沿OQ以速度$v'$行驶时（如图乙所示），在静水中的速度$v_2' ＞ v_2$，则无人艇在静水中的速度大小至少为25.5m/s，C正确。

3. [河北沧州十校2024高一下联考]一船由河岸的A点出发，经过一段时间到达对岸，已知水速为v₁，船在静水中的速度为v₂，两河岸的最近距离为d.可认为河水的水面是水平的.则(C)

A.船到达对岸时的速度一定不等于v₂
B.若v₁＞v₂，船渡河的最小位移为$\frac{\sqrt{v_{1}^{2}+v_{2}^{2}}}{v_{1}}d$
C.若v₂＞v₁，且船渡河的位移最短时，船渡河的时间为$\frac{d}{\sqrt{v_{2}^{2}-v_{1}^{2}}}$
D.船渡河的最短时间为$\frac{d}{\sqrt{v_{1}^{2}+v_{2}^{2}}}$

答案：
3.C　[解析]船到达对岸时的速度为合速度，可能大于、等于或小于船速，故与$v_2$的大小关系不确定，A错误；若$v_1 ＞ v_2$，则当合速度的方向与船速的方向垂直时，船渡河的位移最短，设此时合速度的方向与河岸夹角为$\theta$，则有$\sin \theta = \frac{v_2}{v_1}$，则渡河的最小位移$x = \frac{d}{\sin \theta} = \frac{v_1}{v_2}d$，B错误；若$v_2 ＞ v_1$，则当合速度垂直于河岸时，船渡河的位移最短，此时船渡河的时间为$t = \frac{d}{\sqrt{v_2^2 - v_1^2}}$，C正确；无论船速与水速的关系如何，欲使船渡河的时间最短，都必须使船头垂直于河岸，渡河的最短时间为$t = \frac{d}{v_2}$，D错误。
方法总结 小船渡河的最短时间和最短位移问题
最短时间：不论船速和水速关系如何，最短时间均为船头垂直于河岸时，如图甲所示，$t = \frac{d}{v_{船}}$。

最短位移：$v_{船} ＞ v_{水}$时，合速度垂直于河岸时，位移最短，如图乙所示，$x = d$；$v_{船} \leq v_{水}$时，合速度与船速垂直时，位移最短，如图丙所示，$x = \frac{v_{水}}{v_{船}}d$。

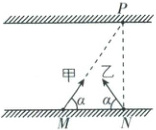
4. [江西宜春2024高一上月考](多选)如图所示，甲、乙两船从一条河流的同一岸边同时开始渡河，河宽为d，M、N分别是甲、乙两船的出发点，其船头与河岸均成α角，甲船船头恰好对准N点的正对岸P点，经过一段时间乙船恰好到达P点，如果两船的速度大小均为v₀，且两船相遇不影响各自的航行.下列判断正确的是(BD)


A.水流方向向左，大小为v₀cosα
B.两船同时到达河对岸，所用时间均为$\frac{d}{v_{0}\sin\alpha}$
C.甲船沿河岸方向的位移大小为$\frac{d}{\sin\alpha}$
D.甲、乙两船会在PN上某点相遇

答案：
4.BD　[解析]以乙船为研究对象，如果水流方向向左，如图1所示，则船的合速度方向为斜向左上，乙船不可能到达P点，则水流方向一定向右，且依题意可知乙船的合速度垂直河岸，则乙船向左的分速度与水流速度大小相等，可得$v_{水} = v_0 \cos \alpha$，故A错误；两船在垂直水流方向上的速度大小均为$v_0 \sin \alpha$，且河宽均为$d$，则两船同时到达河对岸，所用时间均为$t = \frac{d}{v_0 \sin \alpha}$，故B正确；以甲船为研究对象，水流方向向右，如图2所示，则船在水流方向上的速度大小为$v_s = v_{水} + v_0 \cos \alpha = 2v_0 \cos \alpha$，则甲船沿河岸方向的位移大小为$x = v_s t = \frac{2d}{\tan \alpha}$，故C错误；甲、乙两船垂直河岸方向上的速度大小均为$v_0 \sin \alpha$，且这也是乙船的合速度，而甲船还有沿水流方向的速度，即两船在垂直河岸方向上相对静止，而沿水流方向上甲船以$2v_0 \cos \alpha$的速度靠近乙船，且甲船最终会到达P点右侧某位置，所以甲、乙两船会在PN上某点相遇，故D正确。

5. [教材变式][四川凉山州2025高一下期中]假设在某次军事演练时士兵驾驶坦克向东的速度大小为v₁，坦克静止时射出的炮弹速度大小为v₂(v₂＞v₁)，且出膛方向沿水平面内可调整，坦克轨迹距离目标最近为d，炮弹飞行时间极短，忽略炮弹受到的空气阻力和炮弹竖直方向的下落高度，且不计炮弹发射对坦克速度的影响.
(1)若要命中目标且炮弹在空中飞行时间最短，最短时间为多少？坦克发射处离目标的距离为多少？
(2)若到达距离目标最近处时再开炮，求炮弹从发射到命中目标的时间.

答案： 5.
(1)$\frac{d}{v_2}$ $\sqrt{d^2 + (\frac{d v_1}{v_2})^2}$
(2)$\frac{d}{\sqrt{v_2^2 - v_1^2}}$
[解析]
(1)炮弹向北射出时，炮弹在空中飞行时间最短，则（破点：时间最短则炮弹的射出速度垂直于坦克行驶的方向）
最短时间为$t_1 = \frac{d}{v_2}$，
坦克发射处离目标的距离为$x = \sqrt{d^2 + (\frac{d v_1}{v_2})^2}$。
(2)若到达距离目标最近处时再开炮，由于$v_2 ＞ v_1$，应调整炮口至北偏西方向可以射中目标，则炮弹从发射到命中目标的时间为$t_2 = \frac{d}{\sqrt{v_2^2 - v_1^2}}$。
答案及解析
教材变式 本题目由教材P9第3题演变而来。教材考查在击中目标的条件下舰炮的射击方向，本题延伸考查了命中目标时炮弹在空中飞行的最短时间和坦克发射处离目标的距离。