《2026年高中必刷题高中物理必修第二册人教版》

1. 如图所示，从倾角为$\theta$的足够长的斜面顶端$P$以初速度$v_{0}$水平抛出一个小球，落在斜面上$Q$点，小球落在斜面上的速度与斜面的夹角为$\alpha$，若把水平抛出时的初速度变为$2v_{0}$，小球仍落在斜面上，则下列说法正确的是(C)


A.小球落在斜面上的速度与斜面的夹角$\alpha$将变大
B.$PQ$间距变为原来的$2$倍
C.小球做平抛运动的时间变为原来的$2$倍
D.小球落在斜面上的速度大于原来的$2$倍

答案： 1.C 【解析】根据平抛运动规律知$\tan \theta = \frac { y } { x } = \frac { \frac { 1 } { 2 } g t ^ { 2 } } { v _ { 0 } t } = \frac { g t } { 2 v _ { 0 } }$，$\tan ( \alpha + \theta ) = \frac { v _ { y } } { v _ { x } } = \frac { g t } { v _ { 0 } }$，所以$\tan ( \alpha + \theta ) = 2 \tan \theta$，倾角$\theta$为定值，所以小球落在斜面上时速度与斜面的夹角$\alpha$为定值，与速度大小无关，A错误；由上述分析可得$t = \frac { 2 v _ { 0 } \tan \theta } { g }$，小球初速度变为$2v_0$时，做平抛运动的时间变为原来的2倍，C正确；PQ间距$s = \frac { v _ { 0 } t } { \cos \theta } = \frac { 2 v _ { 0 } ^ { 2 } \tan \theta } { g \cos \theta }$，小球初速度变为$2v_0$时，PQ间距变为原来的4倍，B错误；小球落在斜面上时的速度大小$v = \sqrt { v _ { 0 } ^ { 2 } + ( g t ) ^ { 2 } } = \sqrt { v _ { 0 } ^ { 2 } + ( 2 v _ { 0 } \tan \theta ) ^ { 2 } } = v _ { 0 } \sqrt { 1 + 4 \tan ^ { 2 } \theta }$，初速度变为$2v_0$时，落在斜面上时的速度等于原来的2倍，D错误。

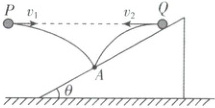
2. [广西南宁 2025 高一下期中]如图，两小球$P$、$Q$从同一高度分别以$v_{1}$和$v_{2}$的初速度水平抛出；都落在了斜面上的$A$点，其中小球$P$垂直打到斜面上，若斜面倾角$\theta = 37^{\circ}$，则$v_{1}$、$v_{2}$大小之比为($\sin 37^{\circ} = 0.6$，$\cos 37^{\circ} = 0.8$)(A)


A.$9:8$
B.$8:9$
C.$32:9$
D.$9:32$

答案： 2.A 【解析】因为两小球从同一高度抛出落到同一点，下落高度相同，根据$h = \frac { 1 } { 2 } g t ^ { 2 }$可知，两球运动时间$t$相等；小球$P$垂直打在斜面上，根据几何关系有$\tan \theta = \frac { v _ { 1 } } { g t }$
关键点：找出$v_1$和$\theta$的关系是解题关键
小球$Q$落在斜面上时，根据几何关系有$\tan \theta = \frac { \frac { 1 } { 2 } g t ^ { 2 } } { v _ { 2 } t } = \frac { g t } { 2 v _ { 2 } }$，联立可得$\frac { v _ { 1 } } { v _ { 2 } } = \frac { 2 \tan ^ { 2 } \theta } { 1 } = \frac { 9 } { 8 }$，故选A。
方法总结：分析平抛运动与斜面结合问题的基本方法若已知位移或初、末位置，则可将位移分解，找出斜面倾角的正切值与水平位移、竖直位移间的关系即可求解；若已知末速度方向，则可将速度分解，利用几何关系求解。

3. (多选)如图所示，光滑的水平桌面上，小球以$v_{0} = 10\ m/s$的初速度从边缘$A$点离开桌面做平抛运动，运动过程中轨迹恰好与放置在水平地面上的半圆柱体相切于$P$点，桌面与地面的高度差为$h$，$BC$是半圆柱体横截面的直径，$B$在$A$的正下方，$O$是半圆柱体横截面的圆心，$OP$与水平面的夹角$\theta = 60^{\circ}$，$g = 10\ m/s^{2}$，则(BC)


A.小球在$P$点时的速度方向与水平方向的夹角为$60^{\circ}$
B.小球从$A$到$P$的运动时间为$\dfrac{\sqrt{3}}{3}\ s$
C.半圆柱体的半径为$\dfrac{20\sqrt{3}}{9}\ m$
D.桌面与地面的高度差为$h = 2.5\ m$

答案： 3.BC 【解析】由几何关系可知，小球在$P$点时的速度方向与水平方向的夹角为$3 0 ^ { \circ }$，故A错误；设小球从$A$点到$P$点的运动时间为$t$，将小球在$P$点时的速度分别沿水平和竖直方向分解，可得$\frac { v _ { 0 } } { g t } = \tan \theta$，解得$t = \frac { \sqrt { 3 } } { 3 } s$，故B正确；小球做平抛
突破点：根据$P$点的速度求时间
运动的水平位移、竖直位移分别为$x = v _ { 0 } t$、$y = \frac { 1 } { 2 } g t ^ { 2 }$，由几何关系可得$R \cos \theta + R = x$，$R \sin \theta + y = h$，联立解得$R = \frac { 2 0 \sqrt { 3 } } { 9 } m$，$h = 5m$，故C正确，D错误。

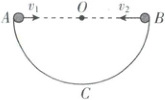
4. [河南许昌高级中学 2025 高一上月考](多选)如图所示为半球形碗的竖直截面图，$O$为圆心，$C$为半球形碗的最低点，$AOB$为水平直径，碗的半径为$r$。两个小球甲和乙先后分别从$A$点、$B$点以不同的初速度$v_{1}$、$v_{2}$沿水平方向相向抛出，小球甲恰好撞到碗上的$C$点，$v_{2} = \dfrac{v_{1}}{2}$。两小球可视为质点，撞到碗后不反弹，忽略空气阻力，重力加速度为$g$。则(BC)


A.两小球能在空中相遇
B.小球乙不可能垂直撞击到碗上
C.小球甲刚要撞到碗时的竖直分速度比乙刚要撞到碗时的竖直分速度大
D.小球乙的初速度$v_{2} = \dfrac{\sqrt{2gr}}{2}$

答案： 4.BC 【解析】两个小球甲和乙是先后做的平抛运动，$h _ { 1 } = \frac { 1 } { 2 } g t _ { 1 } ^ { 2 }$，$h _ { 2 } = \frac { 1 } { 2 } g t _ { 2 } ^ { 2 }$，$t_1$与$t_2$不相同，所以两小球不可能在空中相遇，A错误；由平抛运动推论可知，速度反向延长线一定过水平位移中点，若小球乙垂直撞到碗上，则速度反向延长线应过$O$点，分析可知小球乙速度反向延长线不会过$O$点，则小球乙不可能垂直撞击到碗上，B正确；由平抛运动规律可知，下落高度越大，竖直分速度越大，所以竖直分速度最大时平抛落点为$C$点，由平抛运动规律可得$r = \frac { 1 } { 2 } g t ^ { 2 }$，$r = v _ { 1 } t$，解得$v _ { 1 } = \frac { \sqrt { 2 g r } } { 2 }$，因为$v _ { 2 } = \frac { v _ { 1 } } { 2 }$，所以$v _ { 2 } = \frac { \sqrt { 2 g r } } { 4 }$，C正确，D错误。

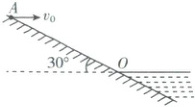
5. [山东滕州一中 2025 高一上月考](多选)如图为湖边一倾角为$30^{\circ}$的大坝的横截面示意图，水面与大坝的交点为$O$。一人站在$A$点处以速度$v_{0}$沿水平方向扔小石块，已知$AO = 40\ m$，重力加速度$g = 10\ m/s^{2}$，忽略人的身高，不计空气阻力。下列说法正确的是(AC)


A.若$v_{0} \geqslant 10\sqrt{3}\ m/s$，则石块平抛运动的时间一定为$2\ s$
B.若$v_{0} = 10\ m/s$，石块平抛运动的时间为$\sqrt{3}\ s$
C.若石块落到斜面上，则石块落到斜面上时速度方向与斜面的夹角与$v_{0}$无关
D.若石块能落入水中，则$v_{0}$越大，落水时速度方向与水平面的夹角越大

答案： 5.AC 【解析】若石块恰落到$O$点，则$A O \cos 3 0 ^ { \circ } = v _ { 0 } t$，$A O \sin 3 0 ^ { \circ } = \frac { 1 } { 2 } g t ^ { 2 }$，可得$t = 2s$，$v _ { 0 } = 1 0 \sqrt { 3 } m / s$，若$v _ { 0 } \geqslant 1 0 \sqrt { 3 } m / s$，则石块一定会落在水平面上，即平抛运动的时间一定为$2s$，A正确；若$v _ { 0 } = 1 0 m / s$，石块将落在斜面上，根据$\tan 3 0 ^ { \circ } = \frac { \frac { 1 } { 2 } g t ^ { 2 } } { v _ { 0 } t } = \frac { g t } { 2 v _ { 0 } }$，可得石块平抛运动的时间为$t = \frac { 2 \sqrt { 3 } } { 3 } s$，B错误；若石块落到斜面上，设石块落到斜面上时速度方向与斜面的夹角为$\alpha$，则有$\tan ( \alpha + 3 0 ^ { \circ } ) = \frac { g t } { v _ { 0 } } = 2 \frac { \frac { 1 } { 2 } g t ^ { 2 } } { v _ { 0 } t } = 2 \tan 3 0 ^ { \circ }$，即$\alpha$为定值，与$v_0$无关，C正确；若石块能落入水中，设落水时速度方向与水平面的夹角为$\beta$，则有$\tan \beta = \frac { v _ { y } } { v _ { 0 } } = \frac { \sqrt { 2 g h } } { v _ { 0 } }$，则$v_0$越大，落水时速度方向与水平面的夹角越小，D错误。
易错分析：本题易忽略落到斜面与落到水面的不同导致错解。物体落到斜面上时，速度方向相同，落到斜面上的不同位置，下落的高度不同，时间不同；物体落到水面上时，下落的高度相同，则下落时间和落到水面上时的竖直速度相同，落到不同的位置，水平速度不同，合速度方向不同。