《2025年锦上添花直击考点与单元双测八年级物理上册人教版》

19. 物理实验小组用口径较小的量筒、天平等器材测量一个石块的密度，由于石块太大不能放入量筒，实验小组采取了如下方法：

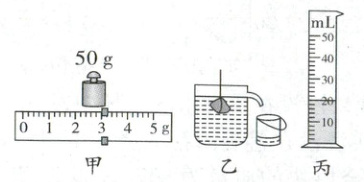
(1)用托盘天平测得石块的质量如图甲所示，石块的质量为53g。
(2)如图乙所示，将石块放入装满(填“满”或“部分”)水的溢水杯中，并用小烧杯接住溢出来的水。
(3)将小烧杯中的水倒入量筒中，测出水的体积(如图丙)，则石块的体积为20 $cm^{3}$。
(4)计算出小石块的密度为2.65 $g/cm^{3}$。
(5)从理论上分析，实验中，由于小烧杯的水不能倒干净，所以测出的石块的密度偏大(填“大”或“小”)。
(6)实验小组的同学还想利用已知密度为 $\rho_{0}$ 的某种液体(该液体不会浸入石块内部)、天平、没有刻度的烧杯、记号笔及其他辅助器材测量石块的密度，实验步骤如下：
① 在烧杯中加入适量的该液体，用天平测出其总质量为 $m_{1}$；
② 将石块放入烧杯内的该液体中，石块被该液体完全浸没，用天平测出其总质量为 $m_{2}$；
③ 用记号笔在烧杯上该液体液面的位置做个标记；
④ 取出石块，向烧杯里加该液体，直到该液体再次到达标记处，用天平测出其总质量为 $m_{3}$；
⑤ 石块密度的表达式 $\rho_{石}=$$\frac{m_2 - m_1}{m_3 - m_1}\rho_0$(用 $m_{1}$、$m_{2}$、$m_{3}$ 及 $\rho_{0}$ 表示)。

答案： 19
(1)53
(2)满
(3)20
(4)2.65
(5)大
(6)向烧杯里加该液体，直到该液体再次到达标记处 $\frac{m_2 - m_1}{m_3 - m_1}\rho_0$ 【解析】为了使该液体和小石块的体积等于最后全部该液体的体积，取出小石块后，向烧杯里加该液体，直到该液体再次到达标记处；加入的液体质量为$\Delta m = m_3 - m_1$，由$\rho = \frac{m}{V}$可知，加入液体的体积为$V_{液体} = \frac{m_3 - m_1}{\rho_0}$；根据题意可知，小石块的体积为$V_{石} = V_{液体} = \frac{m_3 - m_1}{\rho_0}$。由步骤①②可知，小石块的质量为$m_{石} = m_2 - m_1$，由密度公式可得，小石块的密度为$\rho_{石} = \frac{m_{石}}{V_{石}} = \frac{m_2 - m_1}{m_3 - m_1} = \frac{m_2 - m_1}{m_3 - m_1}\rho_0$。

20. 龙门石窟作为世界文化遗产，历史悠久，文化底蕴深厚，如图所示。然而龙门石窟的部分佛像早已伤痕累累、令人心痛。龙门石窟研究院的研究人员通过数字3D打印技术一比一重塑佛首，实现了佛像身首合璧，让千年石窟“活”起来。据了解打印佛首用的材料是光敏树脂，其密度为 $1.3×10^{3}kg/m^{3}$。
（1）若打印佛首用去26kg光敏树脂材料，则此佛首的体积为多少 $m^{3}$？
（2）小洛想知道原佛首的质量，就对龙门石窟附近的石材采样，测得样品质量为16.2g，体积为 $6cm^{3}$，请通过计算判断原佛首的质量为多少kg？

答案： 20解：
(1)根据$\rho = \frac{m}{V}$可得，佛首的体积为$V = \frac{m_{树脂}}{\rho_{树脂}} = \frac{26 kg}{1.3×10^3 kg/m^3} = 0.02 m^3$；
(2)石材的密度$\rho_{石材} = \rho_{样品} = \frac{m_{样品}}{V_{样品}} = \frac{16.2 g}{6 cm^3} = 2.7 g/cm^3 = 2.7×10^3 kg/m^3$，则原佛首的质量$m_{佛首} = \rho_{石材}V = 2.7×10^3 kg/m^3×0.02 m^3 = 54 kg$。答：
(1)此佛首的体积为0.02 m³；
(2)原佛首的质量为54 kg。