第183页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
31. (8分)如图所示,一个质量为300克薄壁长方体容器放在水平硬板CD上,容器底面长15厘米,宽10厘米,容器高度为20厘米,装有10厘米深的水。一根原长为10厘米的轻质的细弹簧AB吊着长方体木块静止,木块下表面刚好与水面接触。弹簧上端A连接着固定不动的支架,下端B连接在木块上表面的中心处,弹簧每拉长或者压缩1厘米需要0.5牛,木块的重力为2.5牛,底面长5厘米,宽5厘米,高度为20厘米。现将水平硬板CD缓慢向上移动,木块始终保持竖直方向,弹簧均在弹性限度内,木块不吸水。求:(g取10牛/千克)
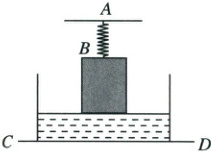
(1)木块的密度。
(2)当木块下表面刚接触容器底部时,水对容器底部压力。
(3)当硬板向上移动22厘米时,容器对硬板的压强值。

(1)木块的密度。
(2)当木块下表面刚接触容器底部时,水对容器底部压力。
(3)当硬板向上移动22厘米时,容器对硬板的压强值。
答案:
31.
(1)木块的体积为$V_木 = 5cm × 5cm × 20cm = 500cm^3$。
由$G = mg$可得,木块的质量为$m_木 = \frac{G_木}{g} = \frac{2.5N}{10N/kg} = 0.25kg = 250g$。
木块的密度为$\rho_木 = \frac{m_木}{V_木} = \frac{250g}{500cm^3} = 0.5g/cm^3$。
答:木块的密度为$0.5g/cm^3$。
(2)当木块下表面刚接触容器底部时,木块浸入的深度$h_1$,而容器中水的体积不变,即$(S_容 - S_木)h_1 = 15cm × 10cm × 10cm$,
代入得$(15cm × 10cm - 5cm × 5cm)h_1 = 150cm^2 × 10cm$,
$h_1 = 12cm < 20cm$,
此时木块受到的浮力$F_浮 = \rho_水 gV_排 = \rho_水 gS_木 h_1 = 1.0 × 10^3kg/m^3 × 10N/kg × 0.05m × 0.05m × 0.12m = 3N$。
弹簧产生的弹力$F_弹 = F_浮 - G = 3N - 2.5N = 0.5N$,
弹簧被压缩的长度$l = \frac{0.5N}{0.5N/cm} = 1cm$,
由水未溢出,则水对容器底的压强$p = \rho_水 gh_1 = 1.0 × 10^3kg/m^3 × 10N/kg × 0.12m = 1.2 × 10^3Pa$。
由$p = \frac{F}{S}$可得,水对容器底部压力$F = pS_容 = 1.2 × 10^3Pa × 15 × 10^{-4}m^2 = 18N$。
答:水对容器底部压力为18N。
(3)容器中水的重力$G_水 = \rho_水 V_水 g = 1.0 × 10^3kg/m^3 × 15 × 10 × 10 × 10^{-6}m^3 × 10N/kg = 15N$。
当硬板向上移动22cm时,弹簧被压缩的长度$\Delta L = 20cm + (10cm - 1cm) - 22cm = 7cm$。
由题可知,此时弹簧对木块的弹力为$F'_弹 = 7cm × 0.5N/cm = 3.5N$,
则容器对硬板的压力$F_压 = G_容 + G_水 + G_木 + F'_弹 = 0.3kg × 10N/kg + 15N + 2.5N + 3.5N = 24N$,
容器对硬板的压强为$p = \frac{F_压}{S} = \frac{24N}{15 × 10^{-4}m^2} = 1.6 × 10^3Pa$。
答:容器对硬板的压强为$1.6 × 10^3Pa$。
(1)木块的体积为$V_木 = 5cm × 5cm × 20cm = 500cm^3$。
由$G = mg$可得,木块的质量为$m_木 = \frac{G_木}{g} = \frac{2.5N}{10N/kg} = 0.25kg = 250g$。
木块的密度为$\rho_木 = \frac{m_木}{V_木} = \frac{250g}{500cm^3} = 0.5g/cm^3$。
答:木块的密度为$0.5g/cm^3$。
(2)当木块下表面刚接触容器底部时,木块浸入的深度$h_1$,而容器中水的体积不变,即$(S_容 - S_木)h_1 = 15cm × 10cm × 10cm$,
代入得$(15cm × 10cm - 5cm × 5cm)h_1 = 150cm^2 × 10cm$,
$h_1 = 12cm < 20cm$,
此时木块受到的浮力$F_浮 = \rho_水 gV_排 = \rho_水 gS_木 h_1 = 1.0 × 10^3kg/m^3 × 10N/kg × 0.05m × 0.05m × 0.12m = 3N$。
弹簧产生的弹力$F_弹 = F_浮 - G = 3N - 2.5N = 0.5N$,
弹簧被压缩的长度$l = \frac{0.5N}{0.5N/cm} = 1cm$,
由水未溢出,则水对容器底的压强$p = \rho_水 gh_1 = 1.0 × 10^3kg/m^3 × 10N/kg × 0.12m = 1.2 × 10^3Pa$。
由$p = \frac{F}{S}$可得,水对容器底部压力$F = pS_容 = 1.2 × 10^3Pa × 15 × 10^{-4}m^2 = 18N$。
答:水对容器底部压力为18N。
(3)容器中水的重力$G_水 = \rho_水 V_水 g = 1.0 × 10^3kg/m^3 × 15 × 10 × 10 × 10^{-6}m^3 × 10N/kg = 15N$。
当硬板向上移动22cm时,弹簧被压缩的长度$\Delta L = 20cm + (10cm - 1cm) - 22cm = 7cm$。
由题可知,此时弹簧对木块的弹力为$F'_弹 = 7cm × 0.5N/cm = 3.5N$,
则容器对硬板的压力$F_压 = G_容 + G_水 + G_木 + F'_弹 = 0.3kg × 10N/kg + 15N + 2.5N + 3.5N = 24N$,
容器对硬板的压强为$p = \frac{F_压}{S} = \frac{24N}{15 × 10^{-4}m^2} = 1.6 × 10^3Pa$。
答:容器对硬板的压强为$1.6 × 10^3Pa$。
32. (10分)钠有多种化合物,如氧化钠、过氧化钠、氢氧化钠、碳酸钠、碳酸氢钠等等,这些物质在实际生活中有广泛的应用,一定条件下相互间能进行如下转化。
2Na₂O₂ + 2CO₂ = 2Na₂CO₃ + O₂↑
2Na₂O₂ + 2H₂O = 4NaOH + O₂↑
2NaOH + CO₂ = Na₂CO₃ + H₂O(CO₂气体适量)
Na₂CO₃ + H₂O + CO₂ = 2NaHCO₃
NaOH + CO₂ = NaHCO₃(CO₂气体过量)
(1)将8.8克二氧化碳与足量的Na₂O₂充分反应,固体质量增加的质量为
(2)将7.8克Na₂O₂完全溶解于93.8克水中,所得溶液的质量百分比浓度为
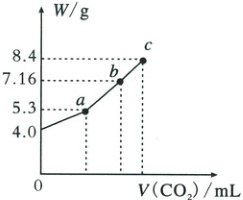
(3)向100mL一定浓度NaOH溶液中通入CO₂充分反应后,在减压和较低温度下,小心地将溶液蒸干,得到白色固体M(不含结晶水)。通入二氧化碳的体积V(标准状况下)与M的质量W的关系如图所示。推断b点时M的组成成分及质量(写出计算过程)。
2Na₂O₂ + 2CO₂ = 2Na₂CO₃ + O₂↑
2Na₂O₂ + 2H₂O = 4NaOH + O₂↑
2NaOH + CO₂ = Na₂CO₃ + H₂O(CO₂气体适量)
Na₂CO₃ + H₂O + CO₂ = 2NaHCO₃
NaOH + CO₂ = NaHCO₃(CO₂气体过量)

(1)将8.8克二氧化碳与足量的Na₂O₂充分反应,固体质量增加的质量为
5.6g
。(2)将7.8克Na₂O₂完全溶解于93.8克水中,所得溶液的质量百分比浓度为
8%
。(3)向100mL一定浓度NaOH溶液中通入CO₂充分反应后,在减压和较低温度下,小心地将溶液蒸干,得到白色固体M(不含结晶水)。通入二氧化碳的体积V(标准状况下)与M的质量W的关系如图所示。推断b点时M的组成成分及质量(写出计算过程)。
答案:
32.
(1)5.6g
(2)8%
(3)由图知$NaOH$质量为4g,物质的量为0.1mol,完全转化为$Na_2CO_3$时,$Na_2CO_3$质量为$0.1mol × \frac{1}{2} × 106g/mol = 5.3g$,完全转化为$NaHCO_3$时,$NaHCO_3$质量为$0.1mol × 84g/mol = 8.4g$,故a点白色固体M为$Na_2CO_3$,c点白色固体M为$NaHCO_3$。由图b点时M的质量为7.16g,$5.3 < 7.16 < 8.4$,由此可知M由$Na_2CO_3$和$NaHCO_3$组成。
设在b点时$Na_2CO_3$物质的量为$x$,$NaHCO_3$物质的量为$y$,则:
$\begin{cases} 2x + y = 0.1, \\ 106x + 84y = 7.16. \end{cases}$
解得$x = 0.02mol$,$y = 0.06mol$,
则$Na_2CO_3$的质量为:$106g/mol × 0.02mol = 2.12g$,
$NaHCO_3$的质量为:$84g/mol × 0.06mol = 5.04g$。
答:b点时M由$Na_2CO_3$和$NaHCO_3$组成,$NaHCO_3$质量为5.04g。
(1)5.6g
(2)8%
(3)由图知$NaOH$质量为4g,物质的量为0.1mol,完全转化为$Na_2CO_3$时,$Na_2CO_3$质量为$0.1mol × \frac{1}{2} × 106g/mol = 5.3g$,完全转化为$NaHCO_3$时,$NaHCO_3$质量为$0.1mol × 84g/mol = 8.4g$,故a点白色固体M为$Na_2CO_3$,c点白色固体M为$NaHCO_3$。由图b点时M的质量为7.16g,$5.3 < 7.16 < 8.4$,由此可知M由$Na_2CO_3$和$NaHCO_3$组成。
设在b点时$Na_2CO_3$物质的量为$x$,$NaHCO_3$物质的量为$y$,则:
$\begin{cases} 2x + y = 0.1, \\ 106x + 84y = 7.16. \end{cases}$
解得$x = 0.02mol$,$y = 0.06mol$,
则$Na_2CO_3$的质量为:$106g/mol × 0.02mol = 2.12g$,
$NaHCO_3$的质量为:$84g/mol × 0.06mol = 5.04g$。
答:b点时M由$Na_2CO_3$和$NaHCO_3$组成,$NaHCO_3$质量为5.04g。
查看更多完整答案,请扫码查看


