《2026年3年中考试卷汇编中考考什么科学浙江专版》

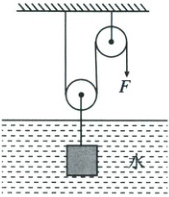
38. (5分)用如图所示的滑轮组匀速提起水中的重物,当重物浸没在水中时,拉力$F$为$11.6\ N$,滑轮组的机械效率为$75\%$,当重物离开水面时,拉力为$14.5\ N$(整个装置的摩擦和绳重不计),求重物的密度。

答案： 38.由图可知，动滑轮上有2股绳，物体浸没在水中时，动滑轮对绳子的拉力为$F_物$，绳端的拉力为$F_拉$，滑轮组的机械效率为75％，根据公式$\eta = \frac{W_有}{W_总} = \frac{F_物h}{F_拉s} = \frac{(G_物 - F_浮)h}{F_拉 × 2h} = \frac{G_物 - F_浮}{2F_拉}$，
则有$75\% = \frac{G_物 - F_浮}{2 × 11.6N}$，
解得$G_物 - F_浮 = 17.4 N$。
又根据公式$F_拉 = \frac{1}{n}(F_物 + G_动)$，
可得$F_拉 = \frac{1}{n}(G_物 - F_浮 + G_动)$，
即$11.6 N = \frac{1}{2}(17.4 N + G_动)$，
解得$G_动 = 5.8 N$。
当物体离开水面时，根据公式$F'_拉 = \frac{1}{n}(G_物 + G_动)$，
可得$14.5 N = \frac{1}{2}(5.8 N + G_物)$，
解得$G_物 = 23.2 N$，
又因为$G_物 - F_浮 = 17.4 N$，
解得$F_浮 = 5.8 N$，
则物体的体积为$V_物 = V_排 = \frac{F_浮}{\rho_水g} = \frac{5.8 N}{1 × 10^3 kg/m^3 × 9.8 N/kg} \approx 5.9 × 10^{-4} m^3$，
物体的密度为$\rho = \frac{m}{V} = \frac{G_物}{gV_物} = \frac{23.2 N}{9.8 N/kg × 5.9 × 10^{-4} m^3} \approx 4 × 10^3 kg/m^3$。
答：重物密度为$4 × 10^3 kg/m^3$。

39. (4分)我很高兴地在家里养了一盆绿色植物,得意地对爸爸说:“我要养在我的小房间里,这样我就可以天天呼吸新鲜空气了!”爸爸却说,晚上植物会和我争夺氧气。爸爸说得对吗?请你设计一个实验帮帮我,看看爸爸说得对还是我说得对,好吗?

答案： 39.爸爸说得对。设计实验：将萌发和煮熟的大豆种子分别放入甲、乙两个广口瓶中密封，一段时间后打开瓶塞，分别放入燃烧的蜡烛，观察蜡烛在瓶中燃烧的情况，如果甲瓶中的蜡烛熄灭，乙瓶蜡烛正常燃烧，则证明植物呼吸消耗氧气。