《2025年同步解析与测评课时练人民教育出版社数学必修第一册人教A版浙江专版》

【例 2】(1)当弓箭手以 a m/s 的速度从地面垂直向上射箭时，t s 后的高度 h m 可由 $ h = at - 5t^2 $ 确定.已知射出 2 s 后箭离地面高 100 m，则弓箭能达到的最大高度为______.

答案：
(1)180m

(2)某租车公司拥有汽车 100 辆，当每辆车的月租金为 3 000 元时，可全部租出，当每辆车的月租金每增加 60 元时，未租出的车将会增加一辆，租出的车每月需要维护费 160 元，未租出的车每月需要维护费 40 元.
①当每辆车的月租金定为 3 900 元时，能租出多少辆车？
②当每辆车的月租金为多少元时，租车公司的月收益最大？最大月收益是多少？

答案：
(2)解：①租金增加了900元，900÷60=15，所以未租出的车有15辆，一共能租出85辆.
②当每辆车的月租金为4560元时，租车公司的最大月收益是324560元.

2.如图所示，已知边长为 8 m 的正方形钢板有一个角被锈蚀，其中 $ AE = 4 $ m，$ CD = 6 $ m.为合理利用这块钢板，在五边形 ABCDE 内截取一个矩形 BNPM，使点 P 在边 DE 上.
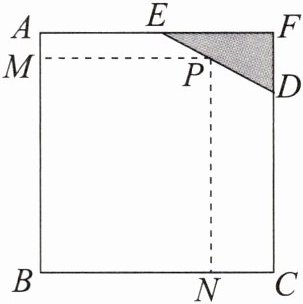
(1)设 $ MP = x $ m，$ PN = y $ m，将 y 表示成 x 的函数，求该函数的解析式及定义域；
(2)求矩形 BNPM 面积的最大值.

答案： 2.解：$(1)y=-\frac{1}{2}x+10，$定义域为{x|4≤x≤8}.
(2)矩形BNPM的面积的最大值为48m².

【例 3】在固定压力差(压力差为常数)下，当气体通过圆形管道时，其流量速率 R(单位：$ cm^3/s $)与管道半径 r(单位：cm)的四次方成正比.比例系数为 $ k(k ＞ 0) $.
(1)试写出气体流量速率 R 关于管道半径 r 的函数解析式；
(2)若气体在半径为 3 cm 的管道中，流量速率为 $ 400 cm^3/s $，求气体通过半径为 r 的管道时，其流量速率 R 的解析式.

答案： 【例3】解：
(1)由题意，可得R=kr⁴(k＞0).
(2)由r=3，R=400，可得$k=\frac{R}{r^{4}}=\frac{400}{81}，$则流量速率R的解析式为$R=\frac{400}{81}r^{4}.$

3.制造印花机的成本 y(单位：元)与印花机的每分钟印花布的长度 x(单位：m)之间有函数关系 $ y = ax^b $，b 称为经济尺度指数.已知制造印花机的经济尺度指数为 2，又知印花机的生产能力达到每分钟印花布 2 000 m 时需投入成本 4 000 000 元，要使生产能力达到每分钟印花布 2 500 m，需投入成本______元.

答案： 3.6250000

【例 4】某公司生产一种电子仪器的固定成本为 20 000 元，每生产一台仪器需增加投入 100 元，已知总收益满足函数：
$ R(x) = \begin{cases} 400x - \dfrac{1}{2}x^2, & 0 \leq x \leq 400, \\ 80 000, & x ＞ 400, \end{cases} $
其中 x(单位：台)是仪器的月产量.
(1)将利润表示为月产量的函数 $ f(x) $；
(2)当月产量为何值时，公司所获利润最大？最大利润为多少元？(总收益 = 总成本 + 利润)

答案： 【解题模型示范】
【过程评价】
【例 4】解：
(1)由题意知总成本为 $ 20 000 + 100x $，从而 $ f(x) = \begin{cases} -\dfrac{1}{2}x^2 + 300x - 20 000, & 0 \leq x \leq 400, \\ 60 000 - 100x, & x ＞ 400. \end{cases} $
(2)当 $ 0 \leq x \leq 400 $ 时，$ f(x) = -\dfrac{1}{2}(x - 300)^2 + 25 000 $，所以当 $ x = 300 $ 时，$ f(x) $ 取得最大值 25 000；当 $ x ＞ 400 $ 时，$ f(x) = 60 000 - 100x $ 是减函数，$ f(x) ＜ 60 000 - 100 × 400 = 20 000 ＜ 25 000 $，所以当 $ x = 300 $ 时，$ f(x) $ 取得最大值 25 000，即当每月生产 300 台仪器时，利润最大，最大利润为 25 000 元.