1. 利用电功普遍适用的公式$W=$
2. 在电阻$R_1$、$R_2$组成的串联电路中,在相同时间内电流通过$R_1$、$R_2$所做的功$W_1$、$W_2$与$R_1$、$R_2$之间的关系是$W_1:W_2=$
$UIt$
和欧姆定律$I = \frac{U}{R}$及其变形式$U = IR$可推导出仅适用于纯电阻性用电器或电路(即将电能全部转化为内能的用电器或电路)的电功公式$W=$$\frac{U^2}{R}t$
和$W=$$I^2Rt$
。2. 在电阻$R_1$、$R_2$组成的串联电路中,在相同时间内电流通过$R_1$、$R_2$所做的功$W_1$、$W_2$与$R_1$、$R_2$之间的关系是$W_1:W_2=$
$R_1:R_2$
;在电阻$R_1$、$R_2$组成的并联电路中,在相同时间内电流通过$R_1$、$R_2$所做的功$W_1$、$W_2$与$R_1$、$R_2$之间的关系是$W_1:W_2=$$R_2:R_1$
。
答案:
1. $UIt$ $\frac{U^2}{R}t$ $I^2Rt$ 2. $R_1:R_2$ $R_2:R_1$
1. 一电热器电阻为$R$,当它两端电压为$U$,通电时间为$t$时,消耗电能为$W$,若要使它消耗的电能为$4W$,则下列方法可行的是 (
A.电阻$R$不变,电压$U$不变,通电时间变为原来的$2$倍
B.电阻$R$减半,电压$U$增大$1$倍,通电时间不变
C.电阻$R$不变,电压$U$增大$1$倍,通电时间不变
D.电阻$R$减半,电压$U$不变,通电时间不变
C
)A.电阻$R$不变,电压$U$不变,通电时间变为原来的$2$倍
B.电阻$R$减半,电压$U$增大$1$倍,通电时间不变
C.电阻$R$不变,电压$U$增大$1$倍,通电时间不变
D.电阻$R$减半,电压$U$不变,通电时间不变
答案:
1.C
2. 如图所示,灯泡$L$和电阻串联后接在电压为$U$的电路中,已知电阻的阻值为$R$,通过电路的电流为$I$,则灯泡在$t$时间内消耗的电能是 (
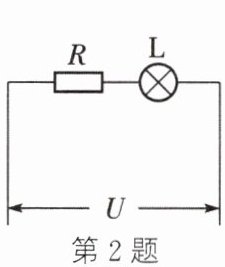
A.$UIt$
B.$\frac{U^2}{R}t$
C.$I^2Rt$
D.$UIt - I^2Rt$
D
)
A.$UIt$
B.$\frac{U^2}{R}t$
C.$I^2Rt$
D.$UIt - I^2Rt$
答案:
2.D
3. 在如图所示的电路中,当闭合开关后,两个电压表指针偏转角度相同,则在相同时间内电流通过电阻$R_1$和$R_2$所做的功之比为 (
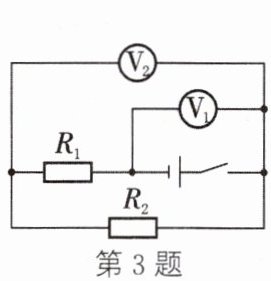
A.$1:5$
B.$5:1$
C.$4:1$
D.$1:4$
C
)
A.$1:5$
B.$5:1$
C.$4:1$
D.$1:4$
答案:
3.C
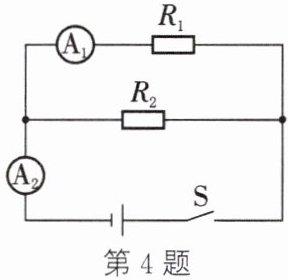
4. 在如图所示的电路中,电阻$R_2 = 20\ \Omega$。$S$闭合后,电流表$A_1$、$A_2$的示数分别为$0.2\ A$和$0.5\ A$。求:
(1) 通电$10\ s$内,电流经过$R_1$、$R_2$时所做的功$W_1$、$W_2$。
(2) 通电$10\ s$内,整个电路消耗的电能。
(1) 通电$10\ s$内,电流经过$R_1$、$R_2$时所做的功$W_1$、$W_2$。
(2) 通电$10\ s$内,整个电路消耗的电能。

答案:
4.
(1) $I_2 = I - I_1 = 0.5A - 0.2A = 0.3A$;
$U = U_1 = U_2 = I_2R_2 = 0.3A × 20\Omega = 6V$;$W_1 = U_1I_1t = 6V × 0.2A × 10s = 12J$;$W_2 = U_2I_2t = 6V × 0.3A × 10s = 18J$
(2) $W = W_1 + W_2 = 12J + 18J = 30J$
(1) $I_2 = I - I_1 = 0.5A - 0.2A = 0.3A$;
$U = U_1 = U_2 = I_2R_2 = 0.3A × 20\Omega = 6V$;$W_1 = U_1I_1t = 6V × 0.2A × 10s = 12J$;$W_2 = U_2I_2t = 6V × 0.3A × 10s = 18J$
(2) $W = W_1 + W_2 = 12J + 18J = 30J$
查看更多完整答案,请扫码查看


