第81页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
学习任务一 单项式乘单项式
情境探究
已知单项式 $7a^{2}b$ 与单项式 $3ab^{2}$ 相乘,即 $7a^{2}b\cdot 3ab^{2}$,如何进行计算?
问题1:单项式 $7a^{2}b$ 可以化为三个单项式的积,即 $$
问题2:单项式 $3ab^{2}$ 可以化为三个单项式的积,即 $$
问题3:$7a^{2}b\cdot 3ab^{2}$ 可以化为单项式的积,即
问题4:根据乘法交换律和结合律,把常数项和同底数幂分别结合,把问题3的结果化为
问题5:根据以上计算,你发现单项式乘单项式,它们的系数和指数有什么规律?
探究归纳
单项式与单项式相乘,把它们的
情境探究
已知单项式 $7a^{2}b$ 与单项式 $3ab^{2}$ 相乘,即 $7a^{2}b\cdot 3ab^{2}$,如何进行计算?
问题1:单项式 $7a^{2}b$ 可以化为三个单项式的积,即 $$
7
$\cdot$$a^{2}$
$\cdot$b
$$。问题2:单项式 $3ab^{2}$ 可以化为三个单项式的积,即 $$
3
$\cdot$a
$\cdot$$b^{2}$
$$。问题3:$7a^{2}b\cdot 3ab^{2}$ 可以化为单项式的积,即
$7\cdot a^{2}\cdot b\cdot 3\cdot a\cdot b^{2}$
。问题4:根据乘法交换律和结合律,把常数项和同底数幂分别结合,把问题3的结果化为
$(7×3)\cdot (a^{2}\cdot a)\cdot (b\cdot b^{2})$
,结果可化为 $21a^{3}b^{3}$
。问题5:根据以上计算,你发现单项式乘单项式,它们的系数和指数有什么规律?
探究归纳
单项式与单项式相乘,把它们的
系数
、同底数幂
分别相乘作为积的因式,对于只在一个单项式里含有的字母,则连同它的 指数
作为积的一个因式。
答案:
问题1:7$a^{2}$b
问题2:3 a$b^{2}$
问题3:$7\cdot a^{2}\cdot b\cdot 3\cdot a\cdot b^{2}$
问题4:$(7×3)\cdot (a^{2}\cdot a)\cdot (b\cdot b^{2})$
$21a^{3}b^{3}$
问题5:系数相乘,同底数幂相乘.
探究归纳
系数 同底数幂 指数
问题2:3 a$b^{2}$
问题3:$7\cdot a^{2}\cdot b\cdot 3\cdot a\cdot b^{2}$
问题4:$(7×3)\cdot (a^{2}\cdot a)\cdot (b\cdot b^{2})$
$21a^{3}b^{3}$
问题5:系数相乘,同底数幂相乘.
探究归纳
系数 同底数幂 指数
学习任务二 单项式乘多项式
情境探究
如图,一个长方形被分割成3个小长方形。
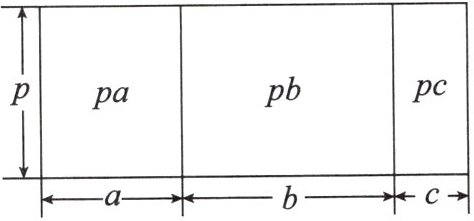
问题1:大长方形的长为 $a + b + c$,宽为 $p$,则这个大长方形的面积为
问题2:图中的三个小长方形的面积分别为
问题3:根据“大长方形的面积和小长方形的面积的数量关系”,可列等式为
探究归纳
单项式与多项式相乘,就是用
情境探究
如图,一个长方形被分割成3个小长方形。

问题1:大长方形的长为 $a + b + c$,宽为 $p$,则这个大长方形的面积为
$p(a+b+c)$
。问题2:图中的三个小长方形的面积分别为
$pa,pb,pc$
。问题3:根据“大长方形的面积和小长方形的面积的数量关系”,可列等式为
$p(a+b+c)=pa+pb+pc$
。探究归纳
单项式与多项式相乘,就是用
单项式
去乘 多项式
的每一项,再把所得的积 相加
。
答案:
问题1:$p(a+b+c)$
问题2:$pa,pb,pc$
问题3:$p(a+b+c)=pa+pb+pc$
探究归纳
单项式 多项式 相加
问题2:$pa,pb,pc$
问题3:$p(a+b+c)=pa+pb+pc$
探究归纳
单项式 多项式 相加
学习任务三 多项式乘多项式
情境探究
如图,长为 $a$ m、宽为 $m$ m 的长方形操场,对其进行扩建,扩建后的操场长增加了 $b$ m,宽增加了 $n$ m。
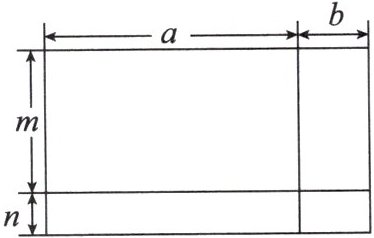
问题1:操场扩建后的长为
问题2:用四个小长方形的面积之和表示总面积为
问题3:根据问题1和问题2可以验证什么等式?
探究归纳
多项式与多项式相乘,先用一个多项式的
情境探究
如图,长为 $a$ m、宽为 $m$ m 的长方形操场,对其进行扩建,扩建后的操场长增加了 $b$ m,宽增加了 $n$ m。

问题1:操场扩建后的长为
$(a+b)$
m,宽为 $(m+n)$
m,所以其面积为 $(a+b)(m+n)$
$m^{2}$。问题2:用四个小长方形的面积之和表示总面积为
$am+an+bm+bn$
。问题3:根据问题1和问题2可以验证什么等式?
$(a+b)(m+n)=am+an+bm+bn$
探究归纳
多项式与多项式相乘,先用一个多项式的
每一项
乘另一个多项式的 每一项
,再把所得的积 相加
。
答案:
问题1:$(a+b)$ $(m+n)$ $(a+b)(m+n)$
问题2:$am+an+bm+bn$
问题3:$(a+b)(m+n)=am+an+bm+bn$.
探究归纳
每一项 每一项 相加
问题2:$am+an+bm+bn$
问题3:$(a+b)(m+n)=am+an+bm+bn$.
探究归纳
每一项 每一项 相加
查看更多完整答案,请扫码查看


