《2025年人教金学典同步解析与测评八年级数学上册人教版云南专版》

3. 如图所示,点 $ M $ 是 $ \angle AOB $($ \angle AOB $ 为锐角)内部的一点。请你在边 $ OA $ 和边 $ OB $ 上分别找到点 $ P $,$ Q $,使得 $ \triangle MPQ $ 的周长最小。

答案：
解:如图,作点M关于OA的对称点M'，点M关于OB的对称点M",连接M'M",交OA于点P，交OB于点Q,此时△MPQ的周长最小.
　　　　　　

4. 如图,点 $ M $,$ N $ 分别是边 $ OA $,$ OB $ 上的定点,点 $ P $,$ Q $ 分别是边 $ OB $,$ OA $ 上的动点,当 $ MP + PQ + QN $ 最小时,作图找出点 $ P $,$ Q $ 的位置。

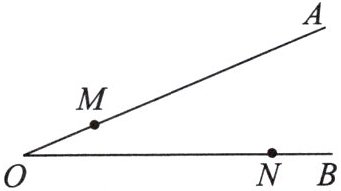
答案：
解:如图,作点M关于OB的对称点E,作点N关于OA的对称点F,连接EF,交OB于点P,交OA于点Q,则点P,Q就是要求作的点.
　　　　　

5. 某重型机械厂旁边有长江和长江支流(如图,假设长江和长江支流的两岸是分别平行的直线),现要在长江和长江支流建两座大桥,大桥必须与长江江堤和长江支流的江堤垂直,使 $ A $ 地人经过两座桥到达 $ B $ 地的路径最短,两座桥应建在何处？

答案：
解:如图.过点A作长江江堤的垂线，截取AA'等于长江的宽,过点B作长江支流江堤的垂线,截取BB'等于长江支流的宽,连接A'B',交长江江堤于点C,交长江支流江堤于点D,过点C作长江江堤的垂线，垂足为E,过点D作长江支流江堤的垂线，垂足为F,CE和DF处即为两座大桥所在的位置.
　　　

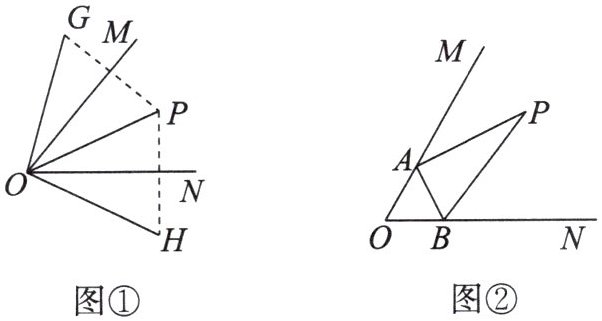
6. 已知点 $ P $ 在 $ \angle MON $ 内。
(1)如图①,点 $ P $ 关于射线 $ OM $ 的对称点是 $ G $,关于射线 $ ON $ 的对称点是 $ H $,连接 $ OG $,$ OH $,$ OP $。若 $ \angle MON = 50^{\circ} $,则 $ \angle GOH = $100°；
(2)如图②,若 $ \angle MON = 60^{\circ} $,$ A $,$ B $ 分别是射线 $ OM $,$ ON $ 上的任意一点,当 $ \triangle PAB $ 的周长最小时,求 $ \angle APB $ 的度数。
图①：
图②：

(2)60°.

答案：
(1)100°　
(2)60°.