《2025年人教金学典同步解析与测评八年级数学上册人教版云南专版》

1. 如图,$\angle ACE= \angle DCE$,$\angle B= 35^{\circ}$,$\angle DCE= 50^{\circ}$,则$\angle A= $( )

A.$65^{\circ}$
B.$75^{\circ}$
C.$85^{\circ}$
D.$95^{\circ}$

答案： A

2. 某款带底座无人机简易模型的示意图如图所示,其中$AB// EF$,$CG\perp EF$,若$\angle ACD= 105^{\circ}$,$\angle B= 69^{\circ}$,则$\angle A+\angle BDC$的度数是( )

A.$15^{\circ}$
B.$21^{\circ}$
C.$36^{\circ}$
D.$48^{\circ}$

答案： C

3. 如图,点$E是\triangle ABC的外角\angle CBD$内部一点,满足$\angle CAB= 3\angle EAB$,$\angle CBD= 3\angle EBD$。若$\angle C= 42^{\circ}$,则$\angle E$的度数是______。

答案： 14°

4. 如图,$CE是\triangle ABC的外角\angle ACD$的平分线,且$CE交BA的延长线于点E$。若$\angle B= m^{\circ}$,$\angle E= n^{\circ}$,则$\angle BAC= $______。(用含$m和n$的式子表示)

答案： m°+2n°

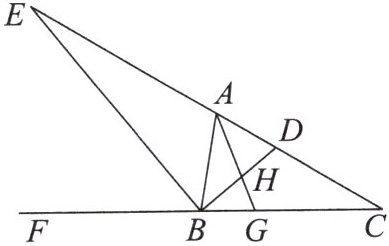
5. 如图,在$\triangle ABC$中,$\angle ABC的平分线交AC于点D$,作$\angle BAG= \angle C$,外角$\angle ABF的平分线交CA的延长线于点E$。
(1) 求证：$BD\perp BE$；
(2) 若$\angle E= 20^{\circ}$,求$\angle AHB$的度数。

答案：
(1)证明:因为∠ABC的平分线交AC于点D,∠ABF的平分线交CA的延长线于点E,所以∠ABD=1/2∠ABC,∠ABE=1/2∠ABF.因为∠ABC+∠ABF=180°,所以∠ABD+∠ABE=1/2(∠ABC+∠ABF)=90°,即BD⊥BE.
(2)解:∠AHB=110°.

6. 如图①,在$\triangle ABC$中,$CD$,$BD分别是\angle ACB和\angle ABC$的平分线,且$\angle A= \alpha$。
(1) 用含$\alpha的式子表示\angle CDB$。
(2) 若把图①中“$CD是\angle ACB$的平分线”改为“$CD是\triangle ABC的外角\angle ACE$的平分线”,如图②,怎样用含$\alpha的式子表示\angle CDB$？
(3) 若把图①中“$CD$,$BD分别是\angle ACB和\angle ABC$的平分线”改成“$CD$,$BD分别是\triangle ABC的外角\angle BCF和\angle CBE$的平分线”,如图③,怎样用含$\alpha的式子表示\angle CDB$？

答案：
(1)∠CDB=90°+1/2α.
(2)∠CDB=1/2α.
(3)∠CDB=90°-1/2α.