《2025年人教金学典同步解析与测评八年级数学上册人教版云南专版》

1. 如图,在方格纸中,点 $ A $,$ B $,$ C $,$ D $,$ E $,$ F $,$ G $ 都在格点上,则 $ \triangle ABC $ 的重心是 ( )

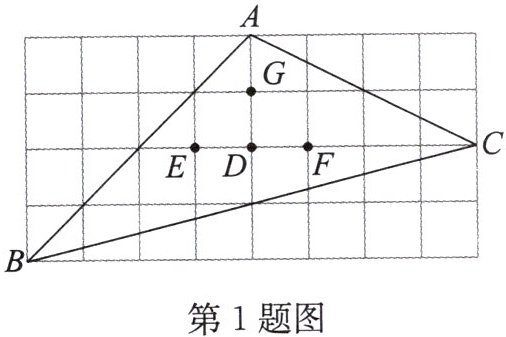
A.点 $ G $
B.点 $ D $
C.点 $ E $
D.点 $ F $

答案： B

2. 如图,在 $ \triangle ABC $ 中,点 $ D $ 是边 $ BC $ 上的一点,且 $ \triangle ABD $ 的面积与 $ \triangle ADC $ 的面积相等,则线段 $ AD $ 为 $ \triangle ABC $ 的 ( )

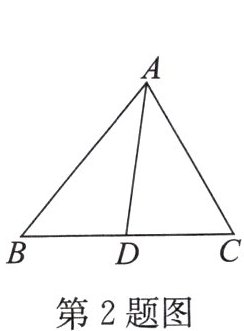
A.高
B.中线
C.角平分线
D.不能确定

答案： B

3. 如图,在 $ \triangle ABC $ 中,$ AD $ 为中线,$ DE $ 和 $ DF $ 分别为 $ \triangle ADB $ 和 $ \triangle ADC $ 的高. 若 $ AB = 3 $,$ AC = 4 $,$ DF = 1.5 $,则 $ DE = $______.

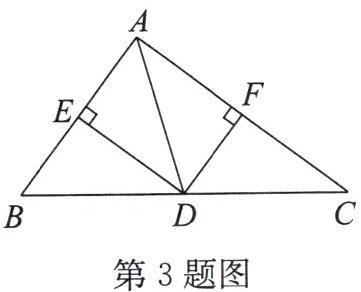
答案： 2

4. 如图,在 $ \triangle ABC $ 中,$ CE $ 平分 $ \angle ACB $,$ \angle 1 = \angle 2 $,若 $ \angle ACE = 23^{\circ} $,则 $ \angle EDC $ 的度数为______.

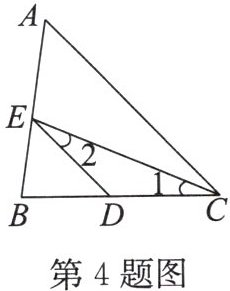
答案： 134°

5. 如图,$ AD $ 为 $ \triangle ABC $ 的中线,$ BE $ 为 $ \triangle ABD $ 的中线.
(1)在 $ \triangle BED $ 中,过顶点 $ E $,$ D $,分别画出 $ BD $,$ BE $ 边上的高 $ EF $,$ DG $；
(2)若 $ \triangle ABC $ 的面积为 $ 40 $,$ BD = 5 $,求 $ \triangle BED $ 的高 $ EF $ 的长.

答案：
解:
(1)如图所示,EF,DG 即为所求.

(2)4.

6. 李叔叔想将如图所示的三角形土地分成面积相等的四块,请你帮他设计至少两种划分方案.

答案：
解:如图①,在△ABC 中,D 为 BC 的中点,E,F 分别为 BD,CD 的中点,连接AD,AE,AF,则$S_{△ABE}=S_{△AED}=S_{△ADF}=S_{△AFC}.$
如图②,在△ABC 中,D,E,F 分别为 BC,AB,AC 的中点,连接 AD,DE,DF,则$S_{△AED}=S_{△AFD}=S_{△BED}=S_{△CFD}.$
如图③,在△ABC 中,D 为 BC 的中点,连接 AD,取 AD 的中点 E,连接 BE,CE,则$S_{△ABE}=S_{△ACE}=S_{△BED}=S_{△CED}.$
如图④,在△ABC 中,D,F 分别为 BC,AC 的中点,连接 AD,DF,取 AD 的中点 E,连接BE,则$S_{△ABE}=S_{△ADF}=S_{△BED}=S_{△FDC}.$
(答案不唯一,只要设计至少两种合理的方案即可)

7. 在等腰三角形 $ ABC $ 中,$ AB = AC $,一腰上的中线 $ BD $ 将这个等腰三角形的周长分成 $ 12 $ 和 $ 6 $ 两部分,求这个等腰三角形的腰长及底边长.

答案： 解:这个等腰三角形的腰长为8,底边长为2.