《2025年人教金学典同步解析与测评八年级数学上册人教版云南专版》

1. 如图,在$\triangle ABC$中,$AB = AC$,且$D为BC$上一点,$CD = AD$,$AB = BD$,则$\angle B$的度数为( )


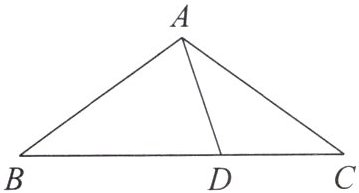
A.$30^{\circ}$
B.$36^{\circ}$
C.$40^{\circ}$
D.$45^{\circ}$

答案： B

2. 如图,在$\triangle ABC$中,$AB = AC$,$BD \perp AC$,垂足为$D$,则$\angle DBC与\angle A$的关系为( )


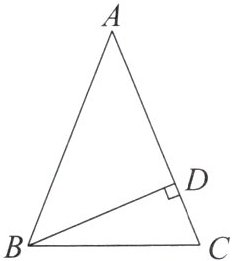
A.$\angle DBC = \angle A$
B.$\angle DBC = 2\angle A$
C.$2\angle DBC = \angle A$
D.无法确定

答案： C

3. 如图,在$\triangle ABC$中,$BE平分\angle ABC$,$DE // BC$,若$AB = 12$,$AD = 5$,则$DE$等于( )


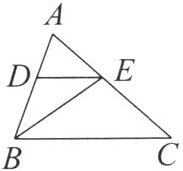
A.$6$
B.$7$
C.$8$
D.$9$

答案： B

4. 如图,在等腰三角形$ABC$中,$AB = AC$,$AB的垂直平分线MN交AC于点D$,$\angle DBC = 15^{\circ}$,则$\angle A$的度数是______.

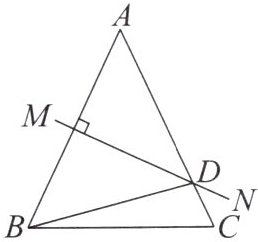
答案： 50°

5. 如图,在$\triangle ABC的BC边上截取BE = AB$,连接$AE$,作$\triangle ABE的角平分线BD交AE于点D$,若$\angle EAC = \angle C$,$BC = 9$,$AB = 5$,则$AD = $______.

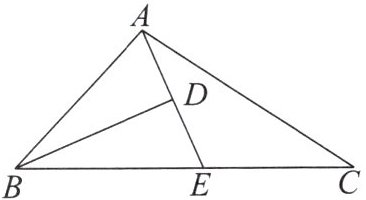
答案： 2

6. 如图,在$\triangle ABC$中,$AB = AC$,$AE是BC$边上的高,$\angle ABC的平分线与AE相交于点D$.求证：点$D在\angle ACB$的平分线上.

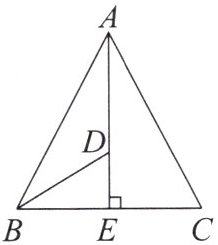
答案：
证明:如图,连接CD. 因为AB=AC,AE是BC边上的高,所以∠BAE=∠CAE.在△BAD和△CAD中,{AB=AC,∠BAE=∠CAE,AD=AD,}所以△BAD≌△CAD(SAS),所以∠ABD=∠ACD.因为AB=AC,所以∠ABC=∠ACB.因为BD是∠ABC的平分线,所以∠ABD=$\frac{1}{2}$∠ABC,所以∠ACD=$\frac{1}{2}$∠ACB,所以点D在∠ACB的平分线上.

7. 如图,在$\triangle ABC$中,$\angle ABC$,$\angle CAB的平分线交于点P$,过点$P作DE // AB$,分别交$BC$,$AC于点D$,$E$.求证：$DE = BD + AE$.

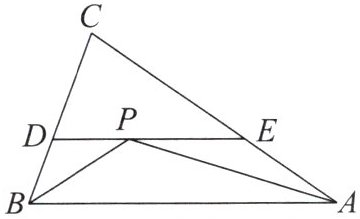
答案： 证明:因为DE//AB,所以∠ABP=∠DPB,∠BAP=∠EPA.因为BP,AP分别平分∠ABC,∠CAB,所以∠ABP=∠DBP,∠BAP=∠EAP,所以∠DBP=∠DPB,∠EAP=∠EPA,所以DP=BD,EP=AE,所以DP+EP=BD+AE,即DE=BD+AE.