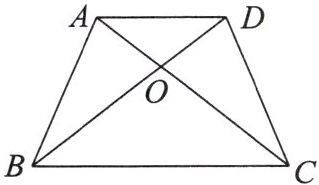
1. 如图所示,$AC= BD$,$AB= CD$,图中全等三角形的对数是( )
A.2
B.3
C.4
D.5

A.2
B.3
C.4
D.5
答案:
B
2. 利用基本作图求作三角形,所作的三角形不唯一的是( )
A.已知三边
B.已知两边和其中一边的对角
C.已知两边和它们的夹角
D.已知两角和一边
A.已知三边
B.已知两边和其中一边的对角
C.已知两边和它们的夹角
D.已知两角和一边
答案:
B
3. 在下列各组条件中,能判定$\triangle ABC和\triangle DEF$全等的是( )
A.$AB= DE$,$BC= EF$,$\angle A= \angle D$
B.$\angle A= \angle D$,$\angle C= \angle F$,$AC= EF$
C.$\angle A= \angle D$,$\angle B= \angle E$,$\angle C= \angle F$
D.$AB= DE$,$BC= EF$,$AC= DF$
A.$AB= DE$,$BC= EF$,$\angle A= \angle D$
B.$\angle A= \angle D$,$\angle C= \angle F$,$AC= EF$
C.$\angle A= \angle D$,$\angle B= \angle E$,$\angle C= \angle F$
D.$AB= DE$,$BC= EF$,$AC= DF$
答案:
D
4. 如图,已知$\angle AOB与\angle EO'F$($\angle AOB>\angle EO'F$),分别以点$O$,$O'$为圆心,以同样长为半径作弧,分别交$OA$,$OB于点A'$,$B'$,交$O'E$,$O'F于点E'$,$F'$。以点$B'$为圆心,以$E'F'$为半径作弧,在$\angle AOB的内部交弧A'B'于点H$。下列结论正确的是( )

A.$\angle AOB= 2\angle EO'F$
B.$\angle AOH= \angle EO'F$
C.$\angle AOH= \angle BOH$
D.$\angle HOB= \angle EO'F$

A.$\angle AOB= 2\angle EO'F$
B.$\angle AOH= \angle EO'F$
C.$\angle AOH= \angle BOH$
D.$\angle HOB= \angle EO'F$
答案:
D
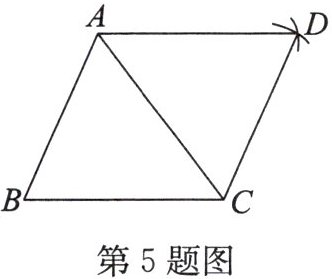
5. 如图,以$\triangle ABC的顶点A$为圆心,以$BC$为半径作弧;再以顶点$C$为圆心,以$AB$为半径作弧,两弧交于点$D$;连接$AD$,$CD$。若$\angle B= 65^{\circ}$,则$\angle ADC$的大小为______。

答案:
65°
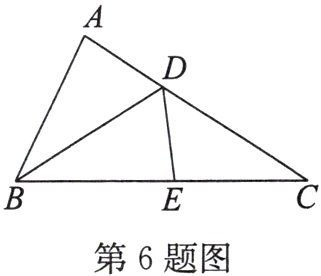
6. 如图,在$\triangle ABC$中,$AD= DE$,$AB= BE$,$\angle A= 83^{\circ}$,则$\angle CED= $______。

答案:
97°
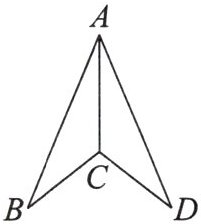
7. 如图,$AB= AD$,$CB= CD$,$\angle B= 30^{\circ}$,$\angle BAD= 46^{\circ}$,则$\angle ACD$的度数是______。

答案:
127°
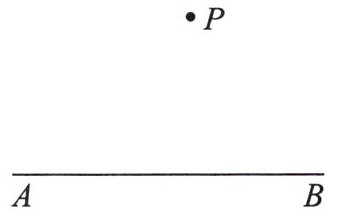
8. 如图,点$P是直线AB$外一点,利用直尺和圆规过点$P作直线AB$的平行线(利用“内错角相等,两直线平行”作图)。

答案:
解:作法:
(1)如图,过点P任意作一条直线EF交AB于点Q;
(2)以点P为角的顶点,PQ为角的一边,作∠CPQ=∠PQB;
(3)反向延长PC,得直线CD,则直线CD//AB.
解:作法:
(1)如图,过点P任意作一条直线EF交AB于点Q;
(2)以点P为角的顶点,PQ为角的一边,作∠CPQ=∠PQB;
(3)反向延长PC,得直线CD,则直线CD//AB.

查看更多完整答案,请扫码查看


