8. (综合与实践)某数学研究小组开展了测量教学楼高度的实践活动,测量方案如下。
|课题|测量教学楼的高度$AB$|
|测量工具|测角仪、皮尺等|
|测量示意图||
|测量说明|如图,$CD\perp DB$,$AB\perp DB$,甲同学在小树$CD与楼AB之间的点E$处,分别测得$\angle AEB= \angle\beta$,$\angle CED= \angle\alpha$,发现$\angle\alpha与\angle\beta$互余|
|测量数据|$BE= DC= 9\mathrm{m}$,$BD= 30\mathrm{m}$|
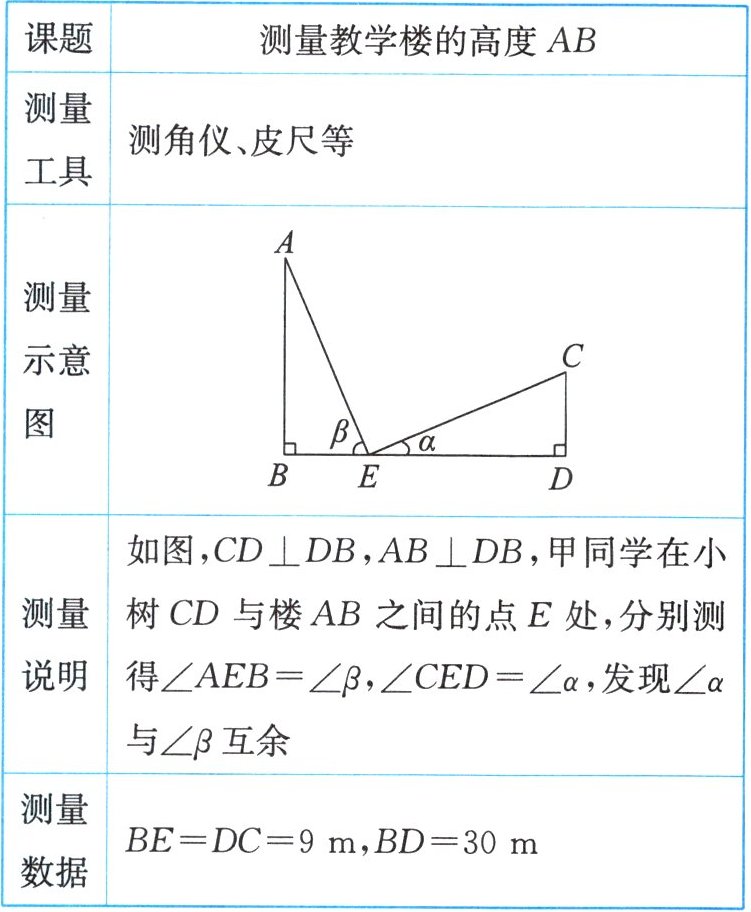
请你根据上述信息求出教学楼的高度$AB$。
|课题|测量教学楼的高度$AB$|
|测量工具|测角仪、皮尺等|
|测量示意图||
|测量说明|如图,$CD\perp DB$,$AB\perp DB$,甲同学在小树$CD与楼AB之间的点E$处,分别测得$\angle AEB= \angle\beta$,$\angle CED= \angle\alpha$,发现$\angle\alpha与\angle\beta$互余|
|测量数据|$BE= DC= 9\mathrm{m}$,$BD= 30\mathrm{m}$|

请你根据上述信息求出教学楼的高度$AB$。
答案:
解:教学楼的高度AB为21m.
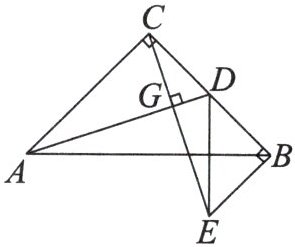
9. 如图,$AC= BC$,$\angle ACB= 90^{\circ}$,点$D为BC$的中点,$BE\perp BC$,$CE\perp AD$,垂足分别为$B$,$G$,那么$AD= CE$,$BD= BE$。这两个结论是否正确?为什么?

答案:
解:这两个结论都是正确的.理由如下:
因为∠ACB=90°,CE⊥AD,
所以∠ECB+∠ACG=90°,∠ACG+
∠DAC=90°.
所以∠ECB=∠DAC.
又因为∠ACB=∠CBE=90°,AC=BC,
所以△ACD≌△CBE(ASA).
所以AD=CE,CD=BE.
又因为D为BC的中点,
所以CD=BD,所以BD=BE.
因为∠ACB=90°,CE⊥AD,
所以∠ECB+∠ACG=90°,∠ACG+
∠DAC=90°.
所以∠ECB=∠DAC.
又因为∠ACB=∠CBE=90°,AC=BC,
所以△ACD≌△CBE(ASA).
所以AD=CE,CD=BE.
又因为D为BC的中点,
所以CD=BD,所以BD=BE.
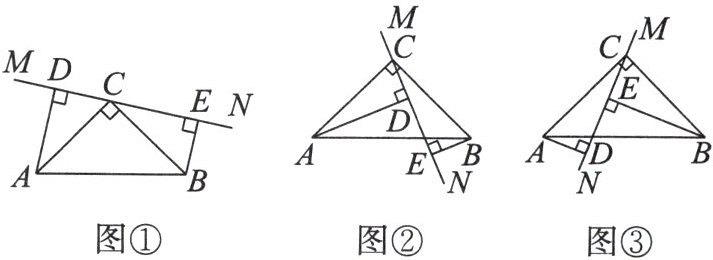
10. 在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= BC$,直线$MN经过点C$,且$AD\perp MN于点D$,$BE\perp MN于点E$。
(1)当直线$MN绕点C$旋转到图①的位置时,求证:①$\triangle ADC\cong\triangle CEB$;②$DE= AD+BE$。
(2)当直线$MN绕点C$旋转到图②的位置时,求证:$DE= AD-BE$。
(3)当直线$MN绕点C$旋转到图③的位置时,$DE$,$AD$,$BE$具有怎样的等量关系?请写出这个等量关系,并说明理由。
(1)当直线$MN绕点C$旋转到图①的位置时,求证:①$\triangle ADC\cong\triangle CEB$;②$DE= AD+BE$。
(2)当直线$MN绕点C$旋转到图②的位置时,求证:$DE= AD-BE$。
(3)当直线$MN绕点C$旋转到图③的位置时,$DE$,$AD$,$BE$具有怎样的等量关系?请写出这个等量关系,并说明理由。

答案:
(1)证明:①因为∠ADC=∠ACB=
∠BEC=90°,
所以∠CAD+∠ACD=90°,∠ACD+
∠BCE=90°.
所以∠CAD=∠BCE.
因为AC=BC,
所以△ADC≌△CEB(AAS).
②由①,知△ADC≌△CEB,
所以AD=CE,CD=BE.
所以DE=CE+CD=AD+BE.
(2)证明:因为∠ADC=∠CEB=
∠ACB=90°,
所以∠ACD=∠CBE.
又因为AC=BC,
所以△ACD≌△CBE(AAS).
所以AD=CE,CD=BE,
所以DE=CE-CD=AD-BE.
(3)解:DE=BE-AD(或AD=BE-
DE,BE=AD+DE).理由如下:
因为∠ADC=∠CEB=∠ACB=90°,
所以∠ACD=∠CBE.
又因为AC=BC,
所以△ACD≌△CBE(AAS).
所以AD=CE,CD=BE,
所以DE=CD-CE=BE-AD.
(1)证明:①因为∠ADC=∠ACB=
∠BEC=90°,
所以∠CAD+∠ACD=90°,∠ACD+
∠BCE=90°.
所以∠CAD=∠BCE.
因为AC=BC,
所以△ADC≌△CEB(AAS).
②由①,知△ADC≌△CEB,
所以AD=CE,CD=BE.
所以DE=CE+CD=AD+BE.
(2)证明:因为∠ADC=∠CEB=
∠ACB=90°,
所以∠ACD=∠CBE.
又因为AC=BC,
所以△ACD≌△CBE(AAS).
所以AD=CE,CD=BE,
所以DE=CE-CD=AD-BE.
(3)解:DE=BE-AD(或AD=BE-
DE,BE=AD+DE).理由如下:
因为∠ADC=∠CEB=∠ACB=90°,
所以∠ACD=∠CBE.
又因为AC=BC,
所以△ACD≌△CBE(AAS).
所以AD=CE,CD=BE,
所以DE=CD-CE=BE-AD.
查看更多完整答案,请扫码查看


