第81页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
含有三个未知数,并且含有未知数的项的次数都是
1
,这样的方程叫作三元一次方程。
答案:
1
共含有三个未知数的三个
拓展 三元一次方程组中的每个方程不一定都含有三个未知数,但方程组中一定要有三个未知数。
一次
方程所组成的一组方程,叫作三元一次方程组。三元一次方程组中各个方程的公共
解,叫作这个三元一次方程组的解。拓展 三元一次方程组中的每个方程不一定都含有三个未知数,但方程组中一定要有三个未知数。
答案:
一次 公共
解三元一次方程组的基本思路是“消元”,即把“三元”化为“二元”,再化为“
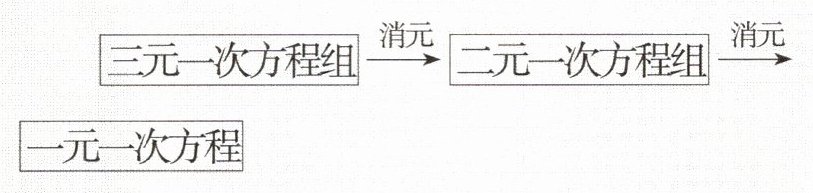
$\begin{matrix}三元一次方程组 & \xrightarrow{消元} & 二元一次方程组 & \xrightarrow{消元} & 一元一次方程\end{matrix}$
一元
”。
$\begin{matrix}三元一次方程组 & \xrightarrow{消元} & 二元一次方程组 & \xrightarrow{消元} & 一元一次方程\end{matrix}$
答案:
一元
【例1】解方程组:$\begin{cases}x + 3y + 2z = 2,①\\3x + 2y - 4z = 3,②\\2x - y = 7。$$③\end{cases}[$听课笔记]
$\begin{matrix}$
$\end{matrix}$
解 ①×2+②,得 5x+8y=7。④
③④组成方程组\begin{cases}2x - y = 7,\\5x + 8y = 7.\end{cases}解这个方程组,得
\begin{cases}x = 3,\\y = -1.\end{cases}把x=3,y=-1代入①,得z=1。
③④组成方程组\begin{cases}2x - y = 7,\\5x + 8y = 7.\end{cases}解这个方程组,得
\begin{cases}x = 3,\\y = -1.\end{cases}把x=3,y=-1代入①,得z=1。
所以原方程组的解是\begin{cases}x = 3,\\y = -1,\\z = 1.\end{cases}
$\begin{matrix}$
$\end{matrix}$
答案:
解 ①×2+②,得 5x+8y=7。④
③④组成方程组$\begin{cases}2x - y = 7,\\5x + 8y = 7.\end{cases}$解这个方程组,得
$\begin{cases}x = 3,\\y = -1.\end{cases}$把x=3,y=-1代入①,得z=1。
所以原方程组的解是$\begin{cases}x = 3,\\y = -1,\\z = 1.\end{cases}$
③④组成方程组$\begin{cases}2x - y = 7,\\5x + 8y = 7.\end{cases}$解这个方程组,得
$\begin{cases}x = 3,\\y = -1.\end{cases}$把x=3,y=-1代入①,得z=1。
所以原方程组的解是$\begin{cases}x = 3,\\y = -1,\\z = 1.\end{cases}$
【对点训练1】解方程组:$\begin{cases}2x + 3y - z = 11,\\2x + y - 5z = 8,\\-2x + 7y + z = 19。$$\end{cases}$
答案:
解$\begin{cases}2x + 3y - z = 11,①\\2x + y - 5z = 8,②\\-2x + 7y + z = 19。$$③\end{cases}$
①+③,得10y=30,即y=3。
②+③,得8y-4z=27。④
将y=3代入④,得$z=-\frac{3}{4}。$
将y=3,$z=-\frac{3}{4}$代入②,得$x=\frac{5}{8}。$
所以原方程组的解是$\begin{cases}x = \frac{5}{8},\\y = 3,\\z = -\frac{3}{4}.\end{cases}$
①+③,得10y=30,即y=3。
②+③,得8y-4z=27。④
将y=3代入④,得$z=-\frac{3}{4}。$
将y=3,$z=-\frac{3}{4}$代入②,得$x=\frac{5}{8}。$
所以原方程组的解是$\begin{cases}x = \frac{5}{8},\\y = 3,\\z = -\frac{3}{4}.\end{cases}$
查看更多完整答案,请扫码查看


