《2025年家庭作业八年级数学上册北师大版》

【例题】某出版社出版一种适合中学生阅读的科普读物，若该读物首次出版印刷的印数不少于$5000$册时，投入的成本与印数的相应数据如下：
(1)经过对上表中数据的探究，发现这种读物的投入成本$y$(单位：元)是印数$x$(单位：册)的一次函数，求这个一次函数表达式(不要求写出$x$的取值范围)；
(2)如果该出版社投入成本$48000$元，那么能印该读物多少册?
[听课笔记]解(1)设所求一次函数表达式为y = kx + b$(k \neq 0)。$由表中数据知，当x = 5000时，y = 28500；当x = 8000时，y = 36000。把它们分别代入函数表达式中，得$\begin{cases}5000k + b = 28500,\\8000k + b = 36000.\end{cases}$解得$\begin{cases}k = \frac{5}{2},\\b = 16000.\end{cases}$所以所求一次函数表达式为$y = \frac{5}{2}x + 16000。$(2)当y = 48000时，$48000 = \frac{5}{2}x + 16000，$解得x = 12800。所以能印该读物12800册。

【名师点拨】用待定系数法求一次函数表达式一般需要两组对应值(或图象上两个点的坐标)，当给出的对应值很多时，要从中选取两组比较简单的，以便于解方程组。

答案： 解
(1)设所求一次函数表达式为$y = kx + b$
$(k \neq 0)$。由表中数据知，当$x = 5000$时，$y = 28500$；
当$x = 8000$时，$y = 36000$。
把它们分别代入函数表达式中，得
$\begin{cases}5000k + b = 28500,\\8000k + b = 36000.\end{cases}$解得$\begin{cases}k = \frac{5}{2},\\b = 16000.\end{cases}$
所以所求一次函数表达式为$y = \frac{5}{2}x + 16000$。
(2)当$y = 48000$时，$48000 = \frac{5}{2}x + 16000$，
解得$x = 12800$。所以能印该读物12800册。

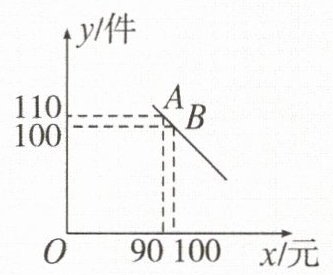
【对点训练】某体育用品商店购进一批球衣，每件的进价为$80$元，出于营销考虑，要求每件球衣的售价不低于$80$元且不高于$150$元，在销售过程中发现，球衣每周的销售量$y$(单位：件)与每件球衣的售价$x$(单位：元)之间满足的函数关系如图所示。
(1)求$y$与$x$之间的函数表达式及$x$的取值范围；
(2)当每件球衣的售价定为$120$元时，每周销售球衣所获利润为多少?

答案： 解
(1)设$y$与$x$之间的函数表达式为
$y = kx + b(k \neq 0)$。将点$A(90,110),B(100,100)$的坐标
分别代入$y = kx + b$，得$\begin{cases}90k + b = 110,\\100k + b = 100.\end{cases}$解得$\begin{cases}k = -1,\\b = 200.\end{cases}$
由题意可知$80 \leq x \leq 150$。故$y$与$x$之间的函数表
达式为$y = -x + 200$，$x$的取值范围为$80 \leq x \leq 150$。
(2)当$x = 120$时，$y = -120 + 200 = 80$，$(120 - 80) ×$
$80 = 3200$(元)。故每周销售球衣所获利润为3200元。

1.已知一次函数$y = kx + b(k \neq 0)$的图象经过点$(2,1)$，$(-5,6)$，用待定系数法求这个一次函数的表达式，可以列出的方程组为(D)。

A.$\begin{cases}2x + y = 1, \\-5x + y = 6\end{cases}$
B.$\begin{cases}2x + 1 = y, \\-5x + 6 = y\end{cases}$
C.$\begin{cases}2k + 1 = b, \\-5k + 6 = b\end{cases}$
D.$\begin{cases}2k + b = 1, \\-5k + b = 6\end{cases}$

答案： 1.D

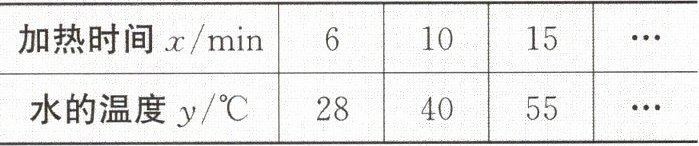
2.在探究“水沸腾时温度变化特点”的实验中，发现在水沸腾前，水的温度$y$(单位：$° C$)与加热时间$x$(单位：$\min$)之间满足一次函数关系，下表记录了实验中水的温度$y$与加热时间$x$变化的部分数据。
则加热$18\min$时水的温度为(B)。

A.$62° C$　　 　
B.$64° C$
C.$66° C$　　 　
D.$68° C$

答案： 2.B