《2025年家庭作业八年级数学上册北师大版》

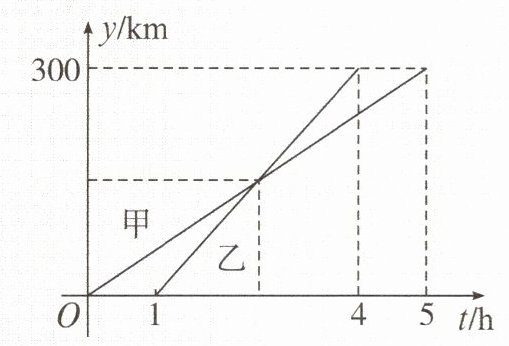
2. 某中学组织八年级学生前往 $A$ 地参加研学活动，学生分为甲、乙两队相继从学校乘车出发，沿同一路线匀速前往 $A$ 地。甲、乙两队离开学校的距离 $y$(单位：$km$)与甲队行驶的时间 $t$(单位：$h$)之间的关系如图所示，则下列结论：①学校与 $A$ 地相距 $300km$；②乙队比甲队晚出发 $1h$，却早到 $1h$；③乙队出发 $2.5h$ 后追上甲队；④甲、乙两队相距 $50km$ 时，$t=\frac{5}{4}$ 或 $\frac{5}{6}$。其中正确的结论有()。


A.$0$ 个
B.$1$ 个
C.$2$ 个
D.$3$ 个
＜ImageHere4＞＜/Img＞

答案： 2.C

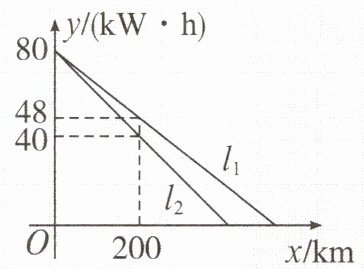
3. 某公司生产了 $A$，$B$ 两款新能源电动汽车。如图，$l_{1},l_{2}$ 分别表示 $A$ 款、$B$ 款新能源电动汽车充满电后电池的剩余电量 $y$(单位：$kW\cdot h$)与汽车行驶路程 $x$(单位：$km$)之间的关系。当两款新能源电动汽车充满电上路行驶，且行驶路程都是 $300km$ 时，$A$ 款新能源电动汽车电池的剩余电量比 $B$ 款新能源电动汽车电池的剩余电量多 $kW\cdot h$。
＜ImageHere5＞＜/Img＞

答案： 3.12

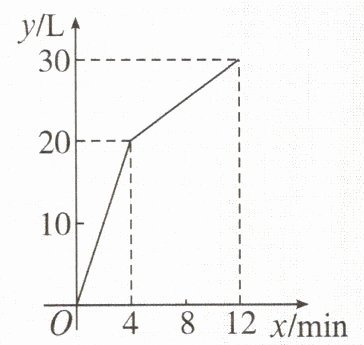
4. 一个装有进水管和出水管的容器，从某时刻开始的 $4min$ 内只进水不出水，在随后的 $8min$ 内既进水又出水，接着关闭进水管直到容器内的水放完。假设每分钟的进水量和出水量是两个常数，容器内的水量 $y$(单位：$L$)与时间 $x$(单位：$min$)之间的部分关系如图所示，那么从关闭进水管起 $min$ 该容器内的水恰好放完。

＜ImageHere6＞＜/Img＞

答案： 4.8

5. 一条笔直的路上依次有 $M$，$P$，$N$ 三地，其中 $M$，$N$ 两地相距 $1000m$。甲、乙两机器人分别从 $M$，$N$ 两地同时出发，匀速前往目的地 $N$，$M$。图中 $OA$，$BC$ 分别表示甲、乙机器人离 $M$ 地的距离 $y$（单位：$m$）与行走时间 $x$（单位：$min$）之间的关系。

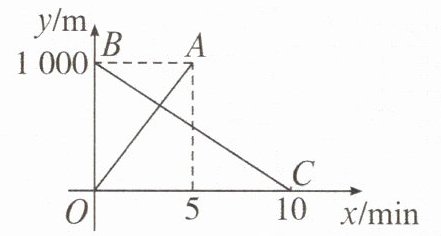
(1)求 $OA$ 所在直线对应的函数表达式；
(2)出发后甲机器人行走多少时间，与乙机器人相遇？
(3)甲机器人到 $P$ 地后，再经过 $1min$ 乙机器人也到 $P$ 地，求 $P$，$M$ 两地间的距离。
＜ImageHere7＞＜/Img＞

答案： 5.解
(1)根据题意，可设$OA$所在直线对应的函数表达式为$y=kx$，将$A(5,1000)$代入，得$1000=5k$，解得$k=200$，所以$y=200x$。
(2)由图可知甲机器人速度为$1000÷5=200(m/min)$，乙机器人速度为$1000÷10=100(m/min)$，两人相遇时$\frac{1000}{100+200}=\frac{10}{3}(min)$，故出发后甲机器人行走$\frac{10}{3}min$，与乙机器人相遇。
(3)设甲机器人行走$t$min时到$P$地，$P$地与$M$地距离为$200t$m，则乙机器人$(t+1)min$后到$P$地，$P$地与$M$地距离为$1000-100(t+1)m$，所以$200t=1000-100(t+1)$，解得$t=3$，所以$200t=200×3=600(m)$，故$P$，$M$两地间的距离为600m。