《2025年家庭作业八年级数学上册北师大版》

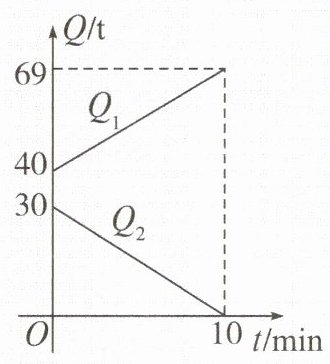
【例题】某空中加油机接到命令，立即给另一架正在飞行的运输飞机进行空中加油。在加油过程中，设运输飞机的油箱余油量为 $Q_{1}$（单位：$t$），空中加油机的加油油箱余油量为 $Q_{2}$（单位：$t$），加油时间为 $t$（单位：$min$），$Q_{1},Q_{2}$ 与 $t$ 之间的关系如图所示。结合图象回答下列问题：
(1)空中加油机的加油油箱中装载了多少吨油？将这些油全部加给运输飞机需多长时间？
(2)求加油过程中，运输飞机的油箱余油量 $Q_{1}$（单位：$t$）与时间 $t$（单位：$min$）之间的关系式；
(3)运输飞机加完油后，以原速度（每分钟耗油量不变）继续飞行，需 $10h$ 到达目的地，油是否够用？说明理由。
[听课笔记]
＜ImageHere1＞＜/Img＞
名师点拨
解答在同一个平面直角坐标系中的两个一次函数图象问题，要善于从两个图象中获取信息，明确各个量的实际意义以及各个量在图象上的体现，注意两个图象涉及的量与量之间的联系，这样便于理解题意及正确解题。

答案： 解
(1)由题中图象知，空中加油机的加油油箱中装载了30t油，全部加给运输飞机需10min。
(2)设$Q_1$与$t$之间的关系式为$Q_1=kt+b$，因为图象过点$(0,40)$和$(10,69)$，所以$40=b$，$69=10k+b$，所以$k=2.9$，$b=40$，所以$Q_1=2.9t+40(0\leq t\leq10)$。
(3)够。由图象知，在加油过程中，运输飞机的油箱余油量由40t到69t，一共增加了29t，所以运输飞机在加油过程10min内消耗掉了1t油。所以每1min的耗油量为$1÷10=0.1(t/min)$。所以10h耗油量为$0.1×10×60=60(t)$。因为$60t＜69t$，所以运输飞机的油够用。

【对点训练】
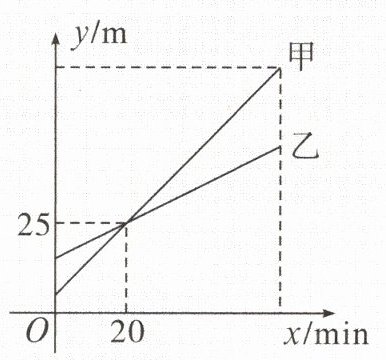
甲、乙两个探测气球分别从海拔 $5m$ 和 $15m$ 处同时出发，匀速上升 $60min$。甲、乙两个探测气球所在位置的海拔 $y$（单位：$m$）与气球上升时间 $x$（单位：$min$）之间的关系如图所示。
(1)求这两个气球在上升过程中 $y$ 与 $x$ 之间的关系式；
(2)当这两个气球的海拔相差 $15m$ 时，求上升的时间。
＜ImageHere2＞＜/Img＞

答案： 解
(1)设甲气球的关系式为$y=kx+b$，乙气球的关系式为$y=mx+n$，分别将$(0,5)$，$(20,25)$和$(0,15)$，$(20,25)$代入，得$b=5$，$20k+b=25$；$n=15$，$20m+n=25$，所以$b=5$，$k=1$；$n=15$，$m=\frac{1}{2}$，所以甲气球上升过程中$y$与$x$之间的关系式为$y=x+5(x\geq0)$，乙气球上升过程中$y$与$x$之间的关系式为$y=\frac{1}{2}x+15(x\geq0)$。
(2)由初始位置，可知当$x＞20$时，两个气球的海拔可能相差15m，且此时甲气球海拔更高，所以$x+5-(\frac{1}{2}x+15)=15$，解得$x=50$，所以当这两个气球的海拔相差15m时，上升的时间为50min。

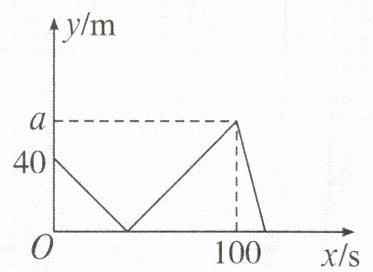
1. 小明、小亮两人相约在公园进行 $500m$ 跑步练习，他们从同一起点出发，先到达终点者原地休息，小明先出发 $10s$，在跑步过程中，小明、小亮两人之间的距离 $y$(单位：$m$)和小亮出发的时间 $x$(单位：$s$)之间的关系如图所示，则图象中 $a$ 的值为()。


A.$50$
B.$60$
C.$70$
D.$80$
＜ImageHere3＞＜/Img＞

答案： 1.B